数学1.3 一元二次方程的根与系数的关系教学演示课件ppt

这是一份数学1.3 一元二次方程的根与系数的关系教学演示课件ppt，共16页。PPT课件主要包含了知识回顾，概括总结，典型例题，拓展延伸，强化纠错，-8k+1＞0，课堂小结，归纳总结，结束寄语，学无止境等内容，欢迎下载使用。

1.一元二次方程的求根公式是什么？
一般地，对于一元二次方程ax2+bx+c=0（a≠0），当b2-4ac≥0时，它的根是
2.用公式法解一元二次方程的一般步骤是什么？
（1）把它化为一般形式，确定a、b、c的值。
（2）再求出b2-4ac的值。
（3）当b2-4ac≥0的前提下，再代入公式求解； 当b2-4ac＜0时，方程无实数解(根) 。
观察上面解一元二次方程的过程，想一想：一元二次方程的根的情况与一元二次方程中二次项系数、一次项系数及常数项有关吗？
可以根据b2-4ac值的符号来判断一元二次方程根的情况。
能否根据这个关系，我们不解方程就能得出方程的解的情况呢？

一元二次方程ax2＋bx＋c = 0（a≠0）的根的情况如下：
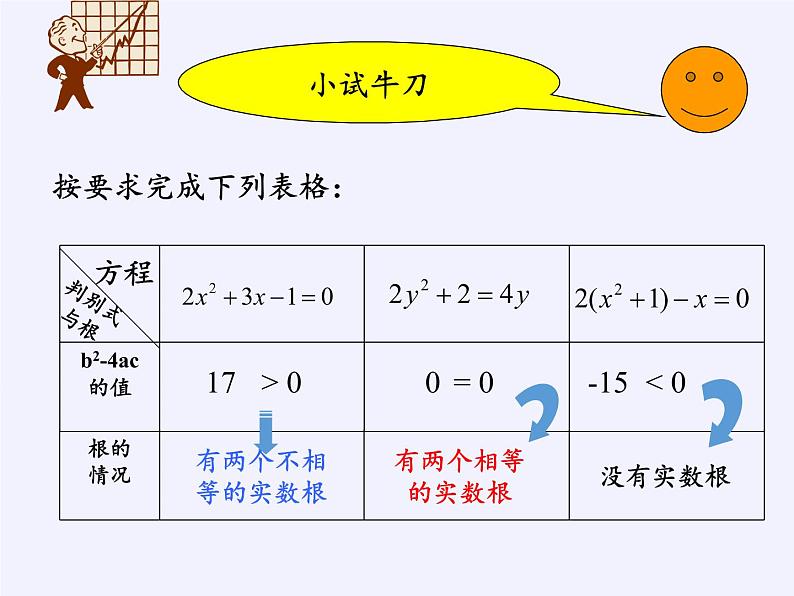
当b2－4ac＞0时，方程有两个不相等的实数根
当b2－4ac = 0时，方程有两个相等的实数根
当b2－4ac ＜ 0时，方程没有实数根
我们把b2－4ac叫做一元二次方程ax2＋bx＋c = 0（a≠0）的根的判别式。
若已知一个一元二次方程的根的情况，是否能得到判别式的值的符号呢？
当方程有两个不相等的实数根时，b2－4ac＞0
当b2－4ac ≥ 0时，方程
当有方程两个相等的实数根时， b2－4ac = 0
当方程没有实数根时， b2－4ac ＜ 0
当方程有两个实数根时， b2－4ac ≥ 0
例1、不解方程，判断下列方程根的情况：（1）-x2+ x-6=0（2）x2+4x=2（3）4x2+1=-3x
解（1）∵a=-1，b= ，c=-6
（2） 移项：x2+4x-2=0
方程要先化为一般形式，再求判别式。
b2-4ac=24-4×（-1）×（-6）=0
∴该方程有两个相等的实数根
∵b2-4ac=16-4×1×（-2）
∴该方程有两个不相等的实数根
例1不解方程，判断下列方程根的情况：（3）4x2+1=-3x
解（3）移项：4x2+3x+1=0
∵b2-4ac=9-4×4×1=9-16=-7＜0
例2：m为何值时，关于x的一元二次方程 2x2-（4m+1）x+2m2-1=0：（1）有两个不相等的实数根？（2）有两个相等的实数根？（3）没有实数根？
解：∵a=2，b=-(4m+1)，c=2m2-1∴b2-4ac=[-(4m+1)]2-4×2(2m2-1)=8m+9
例3 ：m为任意实数，试说明关于x的一元二次方程x2-2mx+4（m-1）=0 恒有两个的实数根。
∴不论m取任何实数，上述方程恒有两个实数根。
∵b2-4ac=(-2m)2-4×1×4（m-1）
=4m2-16（m-1）
=4m2-16m+16
已知：m为任意实数，试说明关于x的方程x2-（m-1）x-3（m+3）=0 恒有两个不相等的实数根。
∵（m+5）2≥0 ∴b2-4ac=（m+5）2+12＞0
∴不论m取任何实数，上述方程总有两个不相等的实数根 。
例4：已知关于x的方程 kx2－(2k＋1)x＋k＋3 = 0 有两个不相等的实数根，求k的取值范围。
解：∵方程有两个不相等的实数根
（2k+1）2-4k（k+3）＞0
4k2+4k+1-4k2-12k＞0
综上所述，k＜ 且k≠0
本节课你有什么收获？谈谈你的感受。
根据b2- 4ac的值的符号，可以确定一元二次方程根的情况。反过来，也可由一元二次方程根的情况来确定b2- 4ac的值的符号。即有：
方程有两个不相等的实数根
方程有两个相等的实数根
若方程有两个实数根，则b2-4ac≥0
一元二次方程的根的情况与系数的关系？