




苏科版九年级上册4.3 等可能条件下的概率(二)课文配套ppt课件
展开1、在具体情境中进一步理解概率的意义,体会概率是描述不确定现象的数学模型。2、进一步理解等可能事件的意义,了解等可能条件下的概率(二)的两个特点--试验结果有无数个和每一个试验结果出现的等可能性。3、能把等可能条件下的概率(二)(能化归为古典概型的几何概型)转化为等可能条件下的概率(一)即古典概型,并能进行简单的计算。
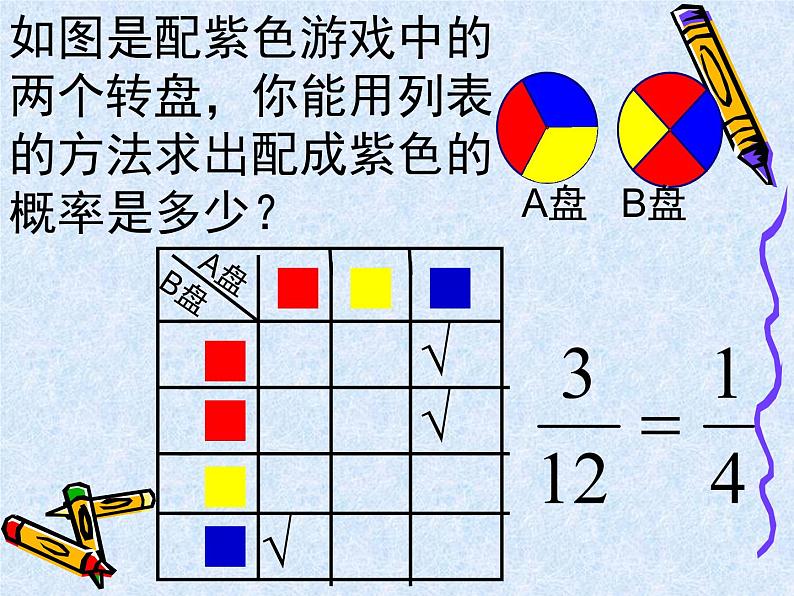
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
A盘 B盘
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
出示一个带指针的转盘,任意转动这个转盘,如果在某个时刻观察指针的位置 。
问题1:这时所有可能结果有多少个?为什么? 问题2:每次观察有几个结果?有无第二个结果? 问题3:每个结果出现的机会是均等的吗?
参考答案:1、无限个,指针可绕过无限个角度。2、一个,第个时刻指针只指向一个位置。3、是的。
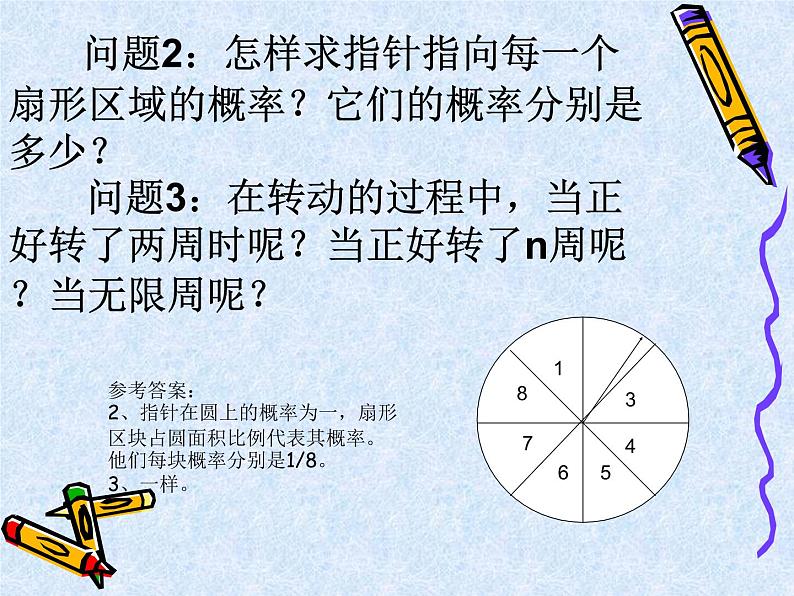
出示一个带指针的转盘,这个转盘被分成8个面积相等的扇形,并标上1、2、3……8,若每个扇形面积为单位1,转动转盘,转盘的指针的位置在不断地改变。
问题1:在转动的过程中当正好转了一周时指针指向每一个扇形区域机会均等吗?那么指针指向每一个扇形区域是等可能性吗?
参考答案:均等,是等可能性。
问题2:怎样求指针指向每一个扇形区域的概率?它们的概率分别是多少? 问题3:在转动的过程中,当正好转了两周时呢?当正好转了n周呢?当无限周呢?
参考答案:2、指针在圆上的概率为一,扇形区块占圆面积比例代表其概率。他们每块概率分别是1/8。3、一样。
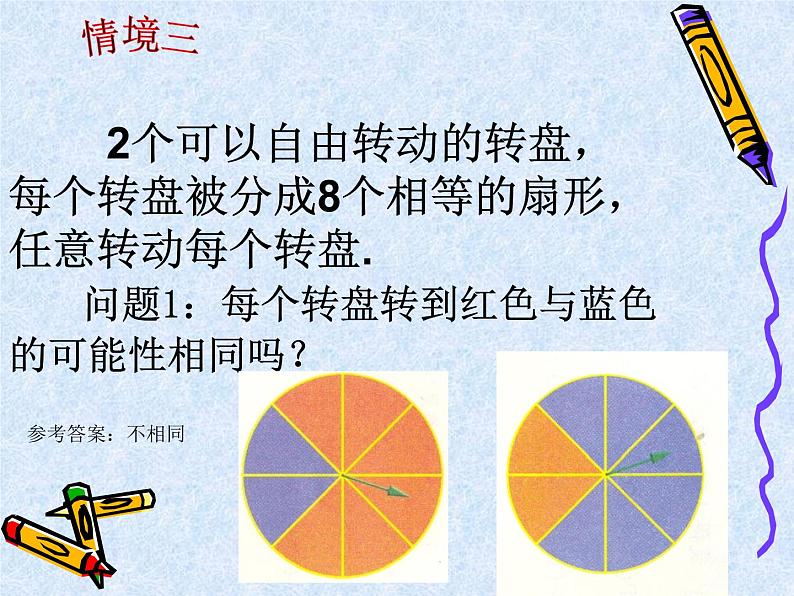
2个可以自由转动的转盘,每个转盘被分成8个相等的扇形,任意转动每个转盘.
问题1:每个转盘转到红色与蓝色的可能性相同吗?
问题2:第一个转盘转一周时,试验结果有几个,其中有几个结果指向红色区域?概率是多少? 问题3:用同样的方法研究第二个转盘,则第二个转盘指向红色区域的概率是多少?
八个,其中六个指向红色区域。概率是3/4
问题4:哪一个转盘指向红色区域概率大?你认为概率大小与什么 因素有直接关系? 问题5:根据上面求概率的方法若要改变这两个转盘指针指向红色区域的概率,需要改变什么?
转盘1,扇形角度有直接关系。
问题6:若把转盘变成正方形其余不变,结果是一样吗?若每个转盘中红色扇形的个数不变,但位置变化一下,结果还是一样吗?
例1:某商场为了吸引顾客,开展有奖销售活动,设立了一个可以自由转动的转盘,转盘等分为16份,其中红色1份、蓝色2份、黄色4份、白色9份,商场规定:顾客每购满1000元的商品,就可获得一次转动转盘的机会,转盘停止时,指针指向红、蓝、黄区域,顾客可分别获得1000元、200元、100元的礼品,某顾客购物1400元,他获得礼品的概率是多少?他分别获得1000元、200元、100元礼品的概率是多少?
参考答案:购物1400元,有一次转盘机会,获得奖品几率为7/16;获1000元,几率为1/16;获200元,几率为1/8;获100元,几率为1/4;
1、说出这位顾客有无获得一次转动转盘的机会?为什么?
2、这个问题在试验过程中共有多少个结果?获得礼品的结果有几种?怎样求获得礼品的概率?
3、用同样的方法可求其余的概率。
4、延伸:若某顾客购满2100元的商品,求获得礼品的概率是多少?两次同时获得1000元礼品的概率是多少?
参考答案:1、收获1次转动转盘的机会。2、四种结果,获得礼品的结果有3种。得奖的格子比总格。3、175/256,1/256.
探索 设计一转盘或方格,使指针或飞标指向红色区域的概率为 ,指针指向黄色区域的概率为 ,指针指向蓝色区域概率为 。
1.等可能条件下的几何概型(转盘、方格)的概率 。2.把等可能条件下,实验结果无限个的几何概型通过等积分割转化为古典概型。
数学九年级上册4.3 等可能条件下的概率(二)教学ppt课件: 这是一份数学九年级上册<a href="/sx/tb_c100299_t3/?tag_id=26" target="_blank">4.3 等可能条件下的概率(二)教学ppt课件</a>,共16页。PPT课件主要包含了知识要点,几何事件的概率,新知导入,看一看,课程讲授,P停在黑砖上,P停在白砖上,随堂练习等内容,欢迎下载使用。
数学九年级上册4.3 等可能条件下的概率(二)课前预习ppt课件: 这是一份数学九年级上册4.3 等可能条件下的概率(二)课前预习ppt课件,共16页。PPT课件主要包含了表格法,第一次,第二次,树状图,活动1,问题1,小结1,活动2,问题2,小结2等内容,欢迎下载使用。
苏科版九年级上册第4章 等可能条件下的概率4.3 等可能条件下的概率(二)课堂教学ppt课件: 这是一份苏科版九年级上册第4章 等可能条件下的概率4.3 等可能条件下的概率(二)课堂教学ppt课件,共19页。PPT课件主要包含了活动1,问题1,小结1,活动2,问题2,小结2,例题解析,巩固应用,拓展延伸等内容,欢迎下载使用。













