新高考2022年高考数学一轮课时跟踪21《同角三角函数的基本关系与诱导公式》练习题

这是一份新高考2022年高考数学一轮课时跟踪21《同角三角函数的基本关系与诱导公式》练习题，共4页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
一、选择题
已知α为锐角，且sinα=eq \f(4,5)，则cs(π＋α)=( )
A.－eq \f(3,5) B.eq \f(3,5) C.－eq \f(4,5) D.eq \f(4,5)
已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,8)))=eq \f(4,5)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(3π,8)))=( )
A.－eq \f(4,5) B.eq \f(4,5) C.－eq \f(3,5) D.eq \f(3,5)
已知α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)π，2π))，且满足cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(2 017,2)π))=eq \f(3,5)，则sinα＋csα=( )
A.－eq \f(7,5) B.－eq \f(1,5) C.eq \f(1,5) D.eq \f(7,5)
已知sin α=eq \f(\r(5),5)，则sin4α－cs4α的值为( )
A.－eq \f(1,5) B.－eq \f(3,5) C.eq \f(1,5) D.eq \f(3,5)
化简=( )
A.sin 2－cs 2 B.sin 2＋cs 2 C.±(sin 2－cs 2) D.cs 2－sin 2
已知sin(π＋θ)=－eq \r(3)cs(2π－θ)，|θ|＜eq \f(π,2)，则θ=( )
A.－eq \f(π,6) B.－eq \f(π,3) C.eq \f(π,6) D.eq \f(π,3)
已知sin2α=eq \f(2,3)，则tanα＋eq \f(1,tanα)=( )
A.eq \r(3) B.eq \r(2) C.3 D.2
若sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－α))=eq \f(1,3)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2π,3)＋2α))等于( )
A.－eq \f(7,9) B.－eq \f(1,3) C.eq \f(1,3) D.eq \f(7,9)
已知α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，2π))，sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))=eq \f(1,3)，则tan(π＋2α)=( )
A.eq \f(4\r(2),7) B.±eq \f(2\r(2),5) C.±eq \f(4\r(2),7) D.eq \f(2\r(2),5)
已知A={sinα，csα，1}，B={sin2α，sinα＋csα，0}，且A=B，
则sin2 023α＋cs2 024α=( )
A.0 B.1 C.－1 D.±1
已知α为锐角，且2tan(π－α)－3cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋β))＋5=0，tan(π＋α)＋6sin(π＋β)=1，则sin α的值是( )
A.eq \f(3 \r(5),5) B.eq \f(3 \r(7),7) C.eq \f(3\r(10),10) D.eq \f(1,3)
已知θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，且sinθ＋csθ=a，其中a∈(0,1)，则tanθ的可能取值是( )
A.－3 B.3或eq \f(1,3) C.－eq \f(1,3) D.－3或－eq \f(1,3)
二、填空题
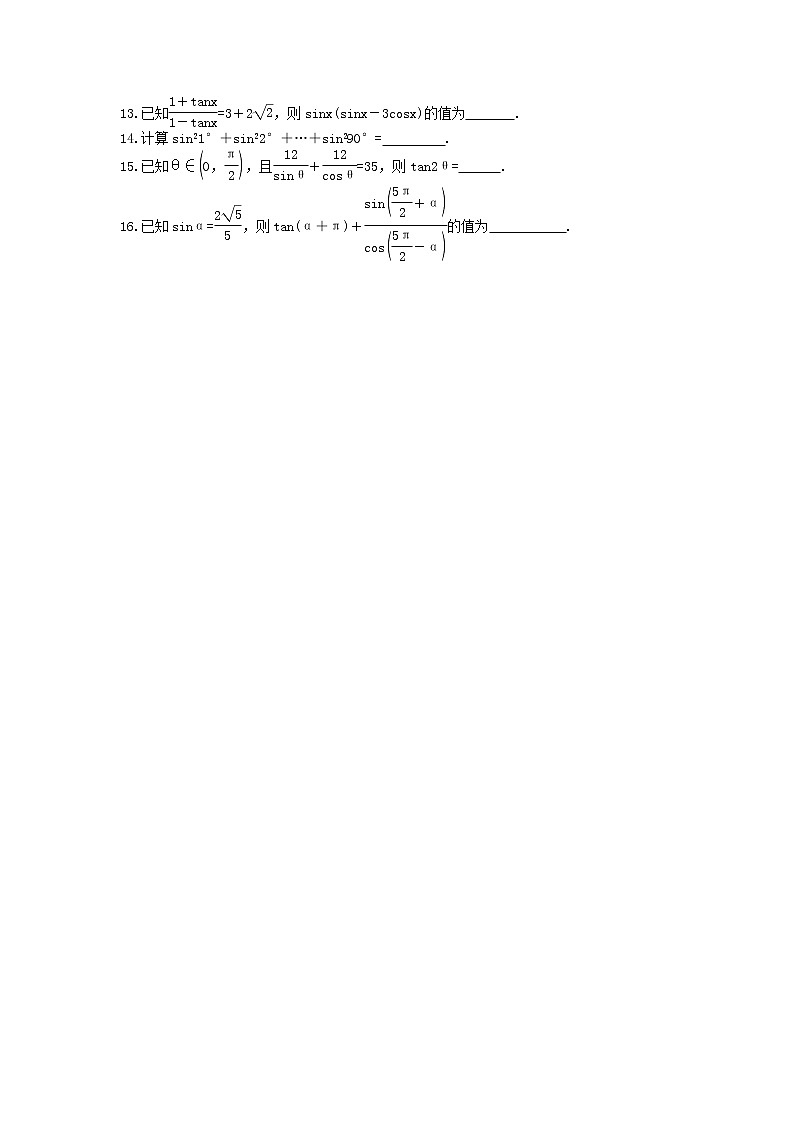
已知eq \f(1＋tanx,1－tanx)=3＋2eq \r(2)，则sinx(sinx－3csx)的值为 .
计算sin21°＋sin22°＋…＋sin290°= .
已知θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，且eq \f(12,sinθ)＋eq \f(12,csθ)=35，则tan2θ= .
已知sinα=eq \f(2\r(5),5)，则tan(α＋π)＋eq \f(sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋α)),cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)－α)))的值为 .
\s 0 答案解析
答案为：A.
解析：∵α为锐角，∴csα=eq \r(1－sin2α)=eq \f(3,5)，∴cs(π＋α)=－csα=－eq \f(3,5)，故选A.
答案为：A.
解析：cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(3π,8)))=cseq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)＋\b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,8)))))=－sineq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,8)))=－eq \f(4,5)，故选A.
答案为：C.
解析：因为cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(2 017,2)π))=csα＋1 008π＋eq \f(π,2)=－sinα=eq \f(3,5)，
且α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)π，2π))，所以sinα=－eq \f(3,5)，csα=eq \r(1－sin2α)=eq \f(4,5)，
则sinα＋csα=－eq \f(3,5)＋eq \f(4,5)=eq \f(1,5).故选C.
答案为：B
解析：sin4α－cs4α=(sin2α－cs2α)(sin2α＋cs2α)
=sin2α－cs2α=2sin2α－1=eq \f(2,5)－1=－eq \f(3,5).
答案为：A
答案为：D
解析：∵sin(π＋θ)=－eq \r(3)cs(2π－θ)，
∴－sin θ=－eq \r(3)cs θ，∴tan θ=eq \r(3).
∵|θ|＜eq \f(π,2)，∴θ=eq \f(π,3).
答案为：C；
解析：tanα＋eq \f(1,tanα)=eq \f(sinα,csα)＋eq \f(csα,sinα)=eq \f(1,sinαcsα)=eq \f(2,sin2α)=eq \f(2,\f(2,3))=3.故选C.
答案为：A；
解析：∵eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋α))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－α))=eq \f(π,2)，
∴sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－α))=sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋α))))=cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋α))=eq \f(1,3).
则cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2π,3)＋2α))=2cs2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)＋α))－1=－eq \f(7,9).
答案为：A；
解析：∵α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，2π))，sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))=eq \f(1,3)，∴csα=eq \f(1,3)，sinα=－eq \f(2\r(2),3)，
由同角三角函数的商数关系知tanα=eq \f(sinα,csα)=－2eq \r(2)，
∴tan(π＋2α)=tan2α=eq \f(2tanα,1－tan2α)=eq \f(－4\r(2),1－－2\r(2)2)=eq \f(4\r(2),7)，故选A.
答案为：C.
解析：当sinα=0时，sin2α=0，此时集合B中不符合集合元素的互异性，故舍去；
当csα=0时，A={sinα，0,1}，B={sin2α，sinα，0}，此时sin2α=1，得sinα=－1，所以sin2 023α＋cs2 024α=－1.
答案为：C
解析：由已知可得－2tan α＋3sin β＋5=0，tan α－6sin β=1，
解得tan α=3，故sin α=eq \f(3\r(10),10).
答案为：C；
解析：由sinθ＋csθ=a，两边平方可得2sinθ·csθ=a2－1.
由a∈(0,1)，得sinθ·csθ＜0.
又∵θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，∴csθ＞0，sinθ＜0，θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0)).
又由sinθ＋csθ=a＞0，知|sinθ|＜|csθ|.
∴θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,4)，0))，从而tanθ∈(－1,0).故选C.
答案为：eq \f(1,3)－eq \r(2).
解析：由eq \f(1＋tanx,1－tanx)=3＋2eq \r(2)得tanx=eq \f(\r(2),2)，
∴sinx(sinx－3csx)=sin2x－3sinxcsx=eq \f(sin2x－3sinxcsx,sin2x＋cs2x)=eq \f(tan2x－3tanx,tan2x＋1)=eq \f(1,3)－eq \r(2).
答案为：45.5；
解析：sin21°＋sin22°＋…＋sin290°
=sin21°＋sin22°＋…＋sin244°＋sin245°＋cs244°＋cs243°＋…
＋cs21°＋sin290°=(sin21°＋cs21°)＋(sin22°＋cs22°)＋…
＋(sin244°＋cs244°)＋sin245°＋sin290°=44＋0.5＋1=40.5.
答案为：±eq \f(24,7).
解析：依题意得12(sinθ＋csθ)=35sinθcsθ，令sinθ＋csθ=t，
∵θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，∴t>0，则原式化为12t=35·eq \f(t2－1,2)，解得t=eq \f(7,5)，故sinθ＋csθ=eq \f(7,5)，
则sinθcsθ=eq \f(12,25)，即eq \f(sinθcsθ,sin2θ＋cs2θ)=eq \f(12,25)，
即eq \f(tanθ,1＋tan2θ)=eq \f(12,25)，12tan2θ－25tanθ＋12=0，解得tanθ=eq \f(3,4)或eq \f(4,3)，
则tan2θ=eq \f(2tanθ,1－tan2θ)=±eq \f(24,7).
答案为：2.5或－2.5.
解：因为sinα=eq \f(2\r(5),5)＞0，所以α为第一或第二象限角.
tan(α＋π)＋eq \f(sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋α)),cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)－α)))=tanα＋eq \f(csα,sinα)=eq \f(sinα,csα)＋eq \f(csα,sinα)=eq \f(1,sinαcsα).
(1)当α是第一象限角时，csα=eq \r(1－sin2α)=eq \f(\r(5),5)，原式=eq \f(1,sinαcsα)=eq \f(5,2).
(2)当α是第二象限角时，csα=－eq \r(1－sin2α)=－eq \f(\r(5),5)，原式=eq \f(1,sinαcsα)=－2.5.
综合(1)(2)知，原式=2.5或－2.5.