人教版新课标A必修33.2.2随机数的产生教案配套课件ppt
展开前面我们在抛硬币的实验中做过大量重复试验,反复计算事件发生的频率,再由频率的稳定值估计概率,但这十分费时,有时还会有破坏性.我们能否找到方法模拟实验解决呢?
1.基本事件、古典概型分别有哪些特点?
基本事件:(1)任何两个基本事件是互斥的;(2)任何事件(除不可能事件)都可以表示成基本事件的和.
古典概型:(1)试验中所有可能出现的基本事件只有有限个(有限性);(2)每个基本事件出现的可能性相等(等可能性).
2 .在古典概型中,事件A发生的概率如何计算?
要产生1-n(n∈N*)之间的随机整数,把n个大小形状完全 相同的小球分别标上1,2,3,…,n,放入一个袋中,把它们充分搅拌,然后从袋中摸出一个,这个球上的数就称为随机数.
如何 产生10个1~100之间的取整数值的随机数?
方法一:抽签法.(1)把100个大小、形状相同的小球分别上号码1,2,3,…,100(2)把这些已经标上号码的小球放到一个袋子中搅拌均匀;(3)从袋子中任意摸出一个小球,这个球上的数就是第一个随机数;(4)不断重复步骤(3)中的操作,即可不断得到个1~100之间的整数值随机数.
思考:抽签法,动手反复做试验;但抽签法花费时间较多,较麻烦.有没有简单省时方法?
计算机或计算器产生的随机数是依照确定算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算机或计算器产生的并不是真正的随机数,称它们为伪随机数。
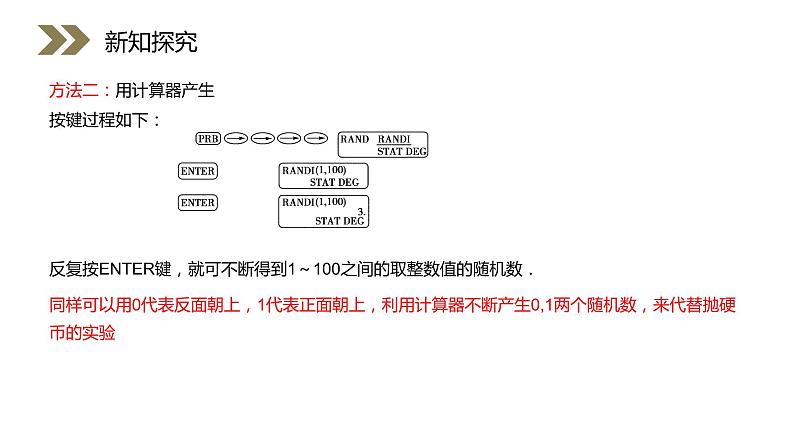
方法二:用计算器产生按键过程如下: 反复按ENTER键,就可不断得到1~100之间的取整数值的随机数.
同样可以用0代表反面朝上,1代表正面朝上,利用计算器不断产生0,1两个随机数,来代替抛硬币的实验
1、选定A1格,键入“=RANDBETWEEN(0,1)”,按Enter键,则在此格中的数是随机产生的0或1。2、选定A1格,按Ctrl+C快捷键,然后选定要随机产生0、1的格,比如A2至A100,按Ctrl+V快捷键,则在A2至A100的数均为随机产生的0或1,这样我们很快就得到了100个随机产生的0,1,相当于做了100次随机试验。3、选定C1格,键入频数函数“=FREQUENCY(A1:A100,0.5)”,按Enter键,则此格中的数是统计A1至A100中,比0.5小的数的个数,即0出现的频数,与就是反面朝上的频数。4、选定D1格,键入“=1-C1/100”,按Enter键,在此格中的数是这100次试验中出现1的频率,即正面朝上的频率。
还可以用计算机产生随机数,而且可以直接统计出频数和频率,以Excel为例,执行下面步骤:
用随机模拟方法估计概率的步骤
上面我们利用计算器或计算机产生的随机数来做模拟试验,通过模拟试验得到的频率来估计概率,这种用计算器或计算机模拟试验的方法称为随机模拟方法或蒙特卡罗方法.
4、常见产生随机数的方法比较
例6 天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?
解:我们通过设计模拟试验的方法来解决问题,利用计算器或计算机可以产生0到9之间去整数值的随机数,我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,这样可以体现下雨的概率是40%。因为是3天,所以每三天随机数作为一组。例如,产生20组随机数
907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989 就相当于作了20次试验。在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两天下雨,他们分别是191,271,932,812,393,即共有5个数。我们得到三天中恰有两天下雨的概率近似5/20=25%
注:这里我们用随机模拟的方法操作简单快捷,但得到只是频率或概率的近似值,而不是概率
1、已知某射击运动员,每次击中目标的概率都是0.8.现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器算出0到9之间取数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
5727 0293 7140 9857 0347 4373 8636 96471417 4698 0371 6233 2616 8045 6011 36619597 7424 6710 4281据此估计,该射击运动员射击4次至少击中3次的概率为( )A.0.85 B.0.812 9C.0.8 D.0.75
2.用随机模拟方法得到的频率( )A.大于概率 B.小于概率C.等于概率 D.是概率的近似值
3.掷两枚骰子,用随机模拟方法估计出现点数之和为10的概率时,产生的整数随机数中,每几个数字为一组( )A.1 D.12
4.通过模拟试验,产生了20组随机数:6830 3013 7055 7430 7740 4422 78842604 3346 0952 6807 9706 5774 57256576 5929 9768 6071 9138 6754如果恰有三个数在1,2,3,4,5,6中,则表示恰有三次击中目标,问四次射击中恰有三次击中目标的概率约为___________.
1.用计算机或计算器产生的随机数,是依照确定的算法产生的数,具有周期性(周期很长),这些数有类似随机数的性质,但不是真正意义上的随机数,称为伪随机数.
2.随机模拟方法是通过将一次试验所有等可能发生的结果数字化,由计算机或计算器产生的随机数,来替代每次试验的结果,其基本思想是用产生整数值随机数的频率估计事件发生的概率,这是一种简单、实用的科研方法,在实践中有着广泛的应用.
高中数学人教版新课标A必修33.2.2随机数的产生集体备课ppt课件: 这是一份高中数学人教版新课标A必修33.2.2随机数的产生集体备课ppt课件,文件包含322ppt、322doc等2份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
高中数学人教版新课标A必修33.2.2随机数的产生复习ppt课件: 这是一份高中数学人教版新课标A必修33.2.2随机数的产生复习ppt课件,共19页。PPT课件主要包含了问题提出,抽签法,用Excel演示,知识迁移,要点分析,小结作业等内容,欢迎下载使用。
高中数学人教版新课标A必修33.2.2随机数的产生备课ppt课件: 这是一份高中数学人教版新课标A必修33.2.2随机数的产生备课ppt课件,共19页。PPT课件主要包含了问题提出,抽签法,用Excel演示,知识迁移,要点分析,小结作业等内容,欢迎下载使用。