必修33.1.3概率的基本性质示范课ppt课件

这是一份必修33.1.3概率的基本性质示范课ppt课件，共42页。PPT课件主要包含了重点与难点，学习目标，事件的关系和运算，事件运算，事件关系，新知探究，集合知识回顾，集合之间的运算，1交集A∩B，A∩B等内容，欢迎下载使用。

1.了解事件间的相互关系；2.理解互斥事件、对立事件的概念；3.会用概率加法公式求某些事件的概率。
重点：事件的关系、运算与概率的性质；难点：事件关系的判定。
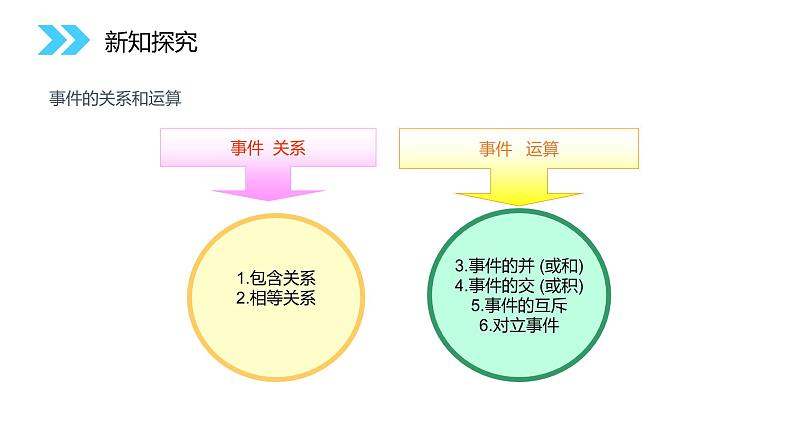
1.包含关系2.相等关系
3.事件的并 (或和)4.事件的交 (或积)5.事件的互斥6.对立事件
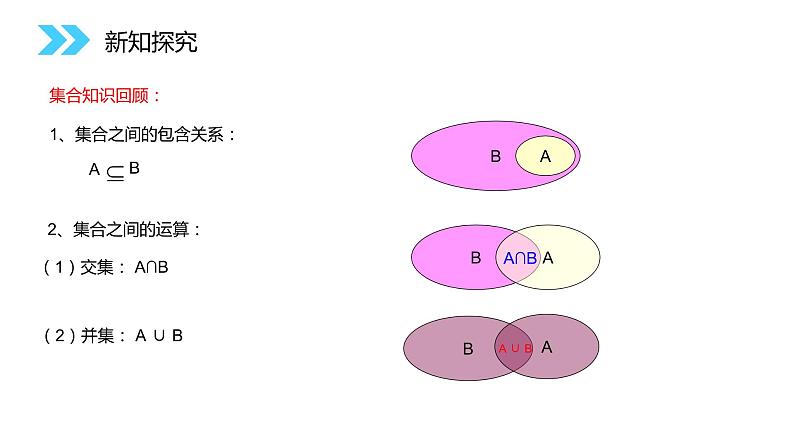
1、集合之间的包含关系：
（2）并集： A ∪ B
（3）补集： CuA
我们知道，一个事件可能包含试验的多个结果。
比如在掷骰子这个试验中：“出现的点数小于或等于3”这个事件中包含了哪些结果呢？
①“出现的点数为1” ②“出现的点数为2” ③“出现的点数为3”这三个结果
这样我们把每一个结果可看作元素，而每一个事件可看作一个集合。因此，事件之间的关系及运算几乎等价于集合之间的关系与运算。
在掷骰子的试验中，我们可以定义许多事件，如：（课本P119）
你能写出这个试验中出现的其它一些事件吗?
如： M ={出现1点或2点}； N1 ={出现的点数小于7}；N2={出现的点数大于4}；
类比集合与集合的关系、运算，探讨它们之间的关系与运算吗？
例：某一学生数学测验成绩记 A = ｛ 95～100分｝ B = ｛优｝，说出A、B之间的关系。
例：事件C1 ={出现1点 }发生，则事件 H ={出现的点数为奇数}也一定会发生，所以
2.等价关系 若事件A发生必有事件B 发生；反之事件B 发生必有事件A 发生即，若A B，且 B A，那么称事件A 与事件B相 等， 记为 A = B
例.事件C1={出现1点}发生，则事件D1={出现的点数不大于1}就一定会发生，反过来也一样，所以C1=D1。
例：从一批产品中抽取30件进行检查, 记 A =｛ 30件产品中至少有1件次品｝，B =｛ 30 件产品中有次品｝。说出A与B之间的关系。
显然事件 A与事件 B 等价记为：A = B
3 . 并事件（或称和事件）若某事件发生当且仅当事件A发生或事件B发生（即 事件A ，B 中至少有一个发生），则称此事件为A与 B的并事件（或和事件） 记为 A B （或 A + B ）。
例: 抽查一批零件, 记事件 A = “都是合格品”， B = “恰有一件不合格品”, C = “至多有一件不合格品”.说出事件A、B、C之间的关系。
4. 交事件（或积事件） 若某事件发生当且仅当事件A发生且事件B发生（即“ A与 B 都发生” ），则称此事件为A 与B 的交事件（或积事件）， 记为A B 或 AB
例：D2=｛出现点数大于3｝， D3= ｛出现点数小于5｝，求D2∩D3.
解：D2=｛出现点数为4,5,6｝， D3=｛出现点数为1,2,3,4｝ D2∩D3=｛出现4点｝。
例：某项工作对视力的要求是两眼视力都在1.01.0以上。记事件 A = “左眼视力在1.0以上” 事件 B =“右眼视力在1.0以上” 事件 C =“视力合格” 说出事件A、B、C的关系。
例、某检查员从一批产品中抽取8件进行检查，观察其中的次品数记：A =“次品数少于5件” ; B = “次品数恰有2件” C = “次品数多于3件” ; D = “次品数至少有1件” 试写出下列事件的基本事件组成： A∪ B ， A ∩C, B∩ C ;
A∪B = A ( A,B 中至少有一个发生）
A∩C= “有4件次品”
5.事件的互斥 若A∩B为不可能事件（ A∩B= ），那么称事件A与事件B互斥，其含义是： 事件A 与 B 在任何一次试验中不会同时发生。
例：抽查一批产品， 事件A =“没有不合格品”， 事件B =“有一件不合格品”，问这两个事件能否在一次抽取中同时发生。
显然，事件A 与事件 B是互斥的，也就是不可能同时发生的。
例1.因为事件C1={出现1点}与事件C2={出现2点}不可能同时发生，故这两个事件互斥；D3={出现的点数小于5}与F={出现的点数大于6}不可能同时发生，故D3与F是互斥事件；G={出现的点数为偶数}与H={出现的点数为奇数}不可能同时发生，故事件G与事件H是互斥事件。
6.对立事件若A∩B为不可能事件，A∪B必然事件，那么称事件A与事件B互为对立事件。其含义是：事件A与事件B在任何一次试验中有且仅有一个发生。
例：从某班级中随机抽查一名学生，测量他的身高，记事件 A =“身高在1.70m 以上”， B =“身高不多于1. 7m ”说出事件A与B的关系。
显然,事件A 与 B互为对立事件
互斥事件是指事件A与事件B在一次试验中不会同时发生，其具体包括三种不同的情形：（1）事件A发生且事件B不发生；（2）事件B发生且事件A不发生；（3）事件A与事件B同时不发生；对立事件是指事件A 与事件B有且仅有一个发生，其包括两种情形；（1）事件A发生B不发生；（2）事件B发生事件A不发生；对立事件是互斥事件的特殊情形。
互斥事件与对立事件的区别与联系：
对立事件一定是互斥事件互斥事件不一定是对立事件如：事件C1与C2是互斥事件，但不是对立事件
例：G={出现的点数为偶数}与H={出现的点数为奇数}G∩H是不可能事件， G∪H是必然事件，故事件G与事件H是对立事件。
区别：互斥事件： 不同时发生，但并非至少有一个发生；对立事件： 两个事件不同时发生，必有一个发生。
2. 从一堆产品（其中正品和次品都多于 2件）中任取 2件，观察正品件数和次品件数，判断下列每对事件是不是互斥事件，若是，再判断它们是不是对立事件：（1）恰好有 1 件次品和恰好有 2 件次品；（2）至少有 1 件次品和全是次品；（3）至少有 1 件正品和至少有 1件次品；（4）至少有 1 件次品和全是正品。
①正正 ②一正一次 ③次次
②、③与③：不互斥不对立
①、②与②、③：不互斥不对立
②、③与①：互斥且对立
3.事件的并 (或和)
4.事件的交 (或积)
5.事件的互斥 (或互不相容)
6.对立事件 (逆事件)
思考：你能说说互斥事件和对立事件的区别吗？
二、概率的几个基本性质
（1）、对于任何事件的概率的范围是： 0≤P（A）≤1 其中必然事件的概率是 P（A）=1 不可能事件的概率是 P（A）=0
思考：概率为1的事件是否为必然事件？ 概率为0的事件是否为不可能事件？
（2）当事件A与事件B互斥时，A∪B的频率 fn(A∪B)= fn(A)+ fn(B) 由此得到概率的加法公式： 如果事件A与事件B互斥，则 P（A∪B）=P（A）+P（B）
注：事件A与B不互斥时，有P（A∪B）=P（A）+P（B）－P（AB)事件A与B互斥时，P（AB）=0，是特殊情况。
例、抛掷骰子，事件A= “出现点数是奇数”， 事件B = “出现点数不超过3”， 求P（A∪B）
解法一：因为P（A）=3/6=1/2，P（B）=3/6=1/2所以P（A∪B）= P（A）+ P（B）=1
解法二：A∪B这一事件包括4种结果，即出现1，2，3和5所以P（A∪B）= 4/6=2/3
概率的加法公式推广：若事件A1，A2，…… ，An彼此互斥，则:
（3）特别地，若事件A与事件B互为对立事件，则A∪B为必然事件，P(A∪B)=1.再由加法公式得 P(A)=1－P(B) ，即
当事件A与事件B是对立事件时，有 P（A）=1－ P（B）
（1）取到红色牌（事件C）的概率是多少？
（2）取到黑色牌（事件D）的概率是多少？
解：（1）因为C= A∪B，且A与B不会同时发生，所以A与B是互斥事件。根据概率的加法公式，得： P（C）=P（A）+P（B）=1/2
（2）C与D也是互斥事件，又由于 C∪D为必然事件，所以C与D互为对立事件，所以 P（D）=1－P（C）=1/2
在求某些事件（如“至多、至少”）的概率时，通常有两种方法：1、将所求事件的概率化为彼此互斥的事件的和，用概率的加法公式求;2、先去求对立事件的概率，进而再求所求事件的概率．
1、一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（ ）至多有一次中靶 B. 两次都不中靶C. 只有一次中靶 D. 两次都不中靶
2、下列各组事件中，不是互斥事件的是（ ） 一个射手进行一次射击，命中环数大于8与命中环数小于6 B. 统计一个班级数学期中考试成绩，平均分数不低于90分与平均分数不高于90分C. 播种菜籽100粒，发芽90粒与发芽80粒 D. 检查某种产品，合格率高于70％与合格率为70％
3.如果某士兵射击一次，未中靶的概率为0.05，求中靶概率。
解：设该士兵射击一次，“中靶”为事件A, “未中靶”为事件B,则A与B互为对立事件， 故P(A)=1-P(B)=1-0.05=0.95。
4.若A，B为互斥事件，则( )(A)P(A)+P(B) <1 (B) P(A)+P(B) >1(C) P(A)+P(B) =1 (D) P(A)+P(B)≤1
5、 某人射击1次，命中率如下表所示：
求射击1次，至少命中7环的概率为_____.
6. 甲，乙两人下棋，若和棋的概率是0.5，乙获胜的概率是0.3 求：（1）甲获胜的概率；（2）甲不输的概率。
解：(1)“甲获胜”是“和棋或乙获胜”的对立事件，因为 “和棋”与“乙获胜”是互斥事件，所以 甲获胜的概率为：1－（0.5+0.3）=0.2 (2)设事件A={甲不输}，B={和棋}，C={甲获胜} 则A=B∪C,因为B,C是互斥事件，所以 P(A)=P(B)+P(C)=0.5+0.2=0.7
7.已知，在一商场付款处排队等候付款的人数及其概率如下：
求至多2个人排队的概率。
解：设事件Ak={恰好有k人排队}， 事件A={至多2个人排队}, 因为A=A0∪A1∪A2,且A0，A1，A2这三个事件是互斥事件， 所以 P(A)=P(A0)+P(A1)+P(A2)=0.1+0.16+0.3=0.56。
8，有10名学生，其中4名男生，6名女生，从中任选2名，求恰好是2名男生或2名女生的概率.
解：记“从中任选2名，恰好是2名男生”为事件A， “从中任选2名，恰好是2名女生”为事件B，则事件A与事件B为互斥事件，且“从中任选2名，恰好是2名男生或2名女生”为事件A+B.
答：从中任选2名，恰好是2名男生或2名女生的概率为7/15.
9，袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为 ，得到黑球或黄球的概率是 ，得到黄球或绿球的概率也是 ，试求得到黑球、得到黄球、得到绿球的概率各是多少？
8、某地区的年降水量在下列范围内的概率如下所示：
1.求年降水量在［100,200）（㎜）范围内的概率；
2.求年降水量在［150,300）（mm)范围内的概率。
解:(1)记这个地区的年降水量在[100,150)，[150,200)，[200,250)，[250,300)(mm)范围内分别为事件为A、B、C、D。
这4个事件是彼此互斥的。根据互斥事件的概率加法公式，有
(1)年降水量在［100,200）(mm)范围内的概率是
P（A＋B）=P(A)+P(B)=0.12+0.25=0.37
(2)年降水量在［150,300）(mm)内的概率是
P(B+C+D)=P(B)+P(C)+P(D)=0.25+0.16+0.14=0.55.
1.事件的关系：包含关系、等价关系； 2.事件的运算：事件的交、并以及对立事件和互斥事件； 3.概率的基本性质及两个互斥事件加法公式的简单运用