《圆的一般方程》人教版高中数学必修二PPT课件（第4.1.2课时）

这是一份人教版新课标A必修2本册综合课文配套课件ppt，共20页。PPT课件主要包含了学习目标，圆的标准方程，Mxy，复习引入，m≠0，新知探究，展开得，圆的一般方程，问题探究1，配方得等内容，欢迎下载使用。

1、正确理解圆的一般方程及其特点
2、能进行圆的一般方程与标准方程的互化
3、回球圆的一般方程及简单的轨迹方程
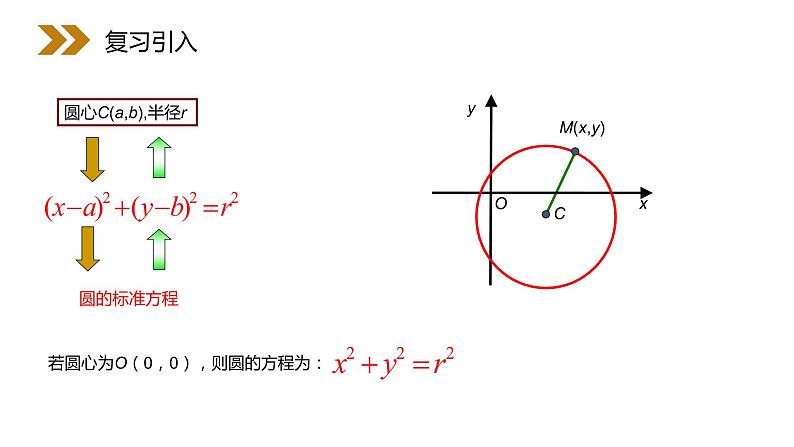
圆心C(a,b),半径r
若圆心为O（0，0），则圆的方程为：
圆心 (2, －4) ，半径
(1) 圆 (x－2)2+ (y+4)2=2
(2) 圆 (x+1)2+ (y+2)2=m2
圆心 (－1, －2) ，半径|m|
分别说出下列圆的圆心与半径:
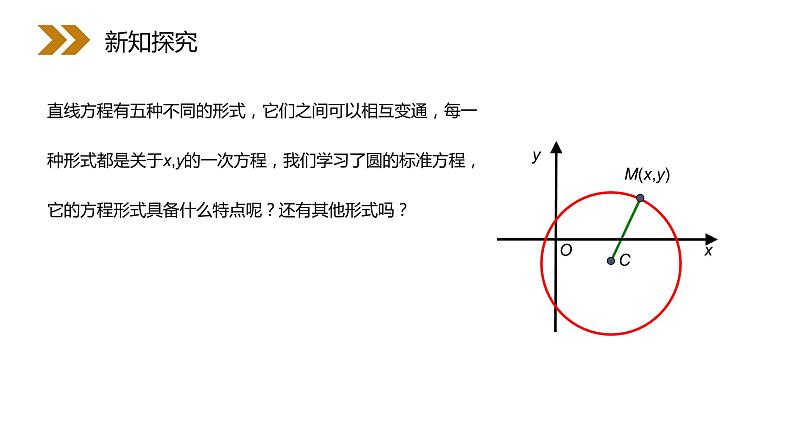
直线方程有五种不同的形式，它们之间可以相互变通，每一种形式都是关于x,y的一次方程，我们学习了圆的标准方程，它的方程形式具备什么特点呢？还有其他形式吗？
任何一个圆的方程都是二元二次方程
结论：任何一个圆方程可以写成下面形式：
以（1，-2）为圆心，以2为半径的圆
（1）当 时，
（2）当 时，
（3）当 时，
注：圆的一般方程的特点:
(3)D2 +E2 -4F＞0
(1)x2 , y2 的系数为1
思考问题:当D=0，E=0或F=0时，圆 的位置分别有什么特点？
(1) x2+y2-2x+4y-4=0
(2) 2x2+2y2-12x+4y=0
(3) x2+2y2-6x+4y-1=0
(4) x2+y2-12x+6y+50=0
(5) x2+y2-3xy+5x+2y=0
圆心（1，-2）半径3
例1.△ABC的三个顶点的坐标分别A(5,1), B(7,－3)，C(2, －8)，求它的外接圆的方程．
由两条弦的中垂线的交点得到圆心，由圆心到圆上一点得到半径
解：设所求圆的方程为：
因为A(5,1),B (7,-3),C(2,-8)都在圆上
把点A，B，C的坐标代入得方程组
归纳：用待定系数法求圆方程的大致步骤：
(1)根据题意，选择标准方程或一般方程。
(2)根据条件列出关于a,b,r或D,E,F的方程组；
(3)解出 a,b,r或D,E,F ，代入标准方程或一般方程。
练习2.证明A(2,2)、B(5,3)、C(3,-1)、D(6,0)四点共圆,并求出此圆的圆心和半径.
设所共圆的方程为x2+y2+Dx+Ey+F=0.
将A、B、D三点坐标代入得
故过A、B、D三点的圆的方程为x2+y2-8x-2y+12=0.
把点C(3,-1)代入方程的左边=9+1-24+2+12=0.
综上,可得四点共圆，圆心为(4,1),半径为 ,方程为x2+y2-8x-2y+12=0.
将方程配方，得(x+1)2+y2=4.
解析：在给定的坐标系中，设M(x，y)是曲线上的任意一点，
由两点的距离公式，上式用坐标表示为
两边平方并化简，得曲线方程 x2+y2+2x-3=0.
∴所求曲线是圆心为C(-1，0)，半径为2的圆.
3.求圆的方程的方法： ①待定系数法；②代入法（几何法）.
（圆心C(a,b),半径r）
求圆心坐标 （两条直线的交点）（常用弦的中垂线）
求半径 （圆心到圆上一点距离）
列关于a，b，r（或D，E，F）的方程组
解出a，b，r（或D，E，F），写出标准方程（或一般方程）