






还剩17页未读,
继续阅读
高中数学人教版新课标A必修2第二章 点、直线、平面之间的位置关系综合与测试授课课件ppt
展开
这是一份高中数学人教版新课标A必修2第二章 点、直线、平面之间的位置关系综合与测试授课课件ppt,共25页。PPT课件主要包含了线面垂直,面面垂直,线线垂直,面面垂直的判定,复习回顾,与AD垂直,不一定,新知探究,垂足为B,∴AB⊥等内容,欢迎下载使用。
(1)利用定义[作出二面角的平面角,证明平面角是直角]
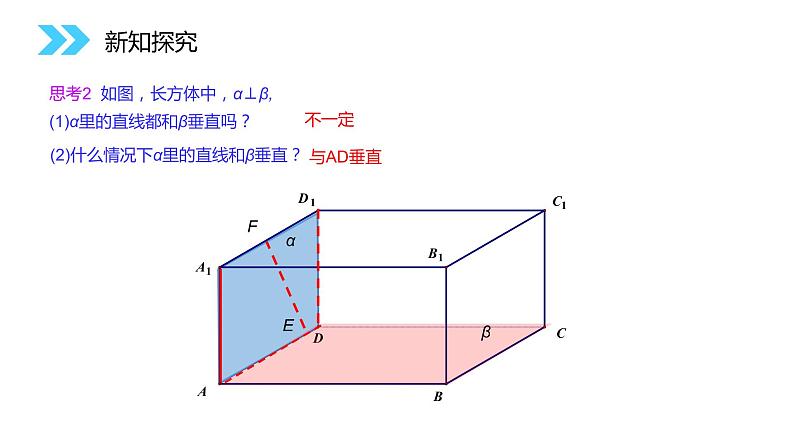
思考2 如图,长方体中,α⊥β,(1)α里的直线都和β垂直吗?
(2)什么情况下α里的直线和β垂直?
思考3 垂足为B,那么直线AB与平面β的位置关系如何? 为什么?
∵ , ∴AB⊥BE.
又由题意知AB⊥CD,且BE CD=B
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
(线是一个平面内垂直于两平面交线的一条直线)
作用: ①它能判定线面垂直. ② 它能在一个平面内作与这个平面垂 直的垂线.
思考4 设平面 ⊥ 平面 ,点P在平面 内,过点P作平面 的垂线a,直线a与平面 具有什么位置关系?
直线a在平面 内
在γ内过A点作直线 a ⊥n,
在γ内过A点作直线 b⊥m,
在γ内任取一点A(不在m,n上),
如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
判断线面垂直的两种方法:①线线垂直→线面垂直;②面面垂直→线面垂直.
例题1 如图4,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在平面,D、E分别是VA、VC的中点,直线 DE与平面VBC有什么关系?试说明理由.
解:由VC垂直于⊙O所在平面,知VC⊥AC,VC⊥BC,即 ∠ACB是二面角A-VC-B的平面角.由∠ACB是直径上的圆周角,知 ∠ACB =90°。
因此,平面 VAC⊥平面VBC.由DE是△VAC两边中点连线,知 DE∥AC,故DE⊥VC.由两个平面垂直的性质定理,知直线DE与平面VBC垂直。
注意:本题也可以先推出AC垂直于平面VBC,再由DE∥AC,推出上面的结论。
例2.S为三角形ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC。 求证:AB⊥BC。
证明:过A点作AD⊥SB于D点.∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC,∴ AD⊥BC.
又∵ SA ⊥ 平面ABC, ∴SA ⊥ BC. AD∩SA=A∴BC ⊥ 平面SAB.∴BC ⊥AB.
练习1:如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。
2.如图,平面AED ⊥平面ABCD,△AED是等边三角形,四边形ABCD是矩形,
(1)求证:EA⊥CD
(2)若AD=1,AB= ,求EC与平面ABCD所成的角。
(2012·北京模拟)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(1)求证:BM∥平面ADEF;(2)求证:平面BDE⊥平面BEC.
证明:(1)取DE中点N,连接MN,AN.在△EDC中,M,N分别为EC,ED的中点,所以MN//CD,且MN= CD.由已知AB//CD,AB= CD,所以MN//AB,且MN=AB,所以四边形ABMN为平行四边形.所以BM//AN.又因为AN平面ADEF,且BM 平面ADEF,所以BM//平面ADEF.
(2)因为四边形ADEF为正方形,所以ED⊥AD,又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD.又因为EDB 平面ADEF,所以ED⊥平面ABCD.所以ED⊥BC.
在直角梯形ABCD中,AB=AD=2,CD=4,可得BC= ,在△BCD中,BD=BC= ,CD=4,所以BC⊥BD,BD∩ED=D,所以BC⊥平面BDE,又因为BC 平面BCE,所以平面BDE⊥平面BEC.
(4)已知面面垂直易找面的垂线,且在某一个平面内
(5) 解题过程中应注意充分领悟、应用
(3) 证明面面垂直要从寻找面的垂线入手
(2) 理解面面垂直的判定与性质都要依赖面面垂直的定义
(1) 定义面面垂直是在建立在二面角的定义的基础上的
2.面面垂直的性质推论:
1.平面与平面垂直的性质定理:
(1)利用定义[作出二面角的平面角,证明平面角是直角]
思考2 如图,长方体中,α⊥β,(1)α里的直线都和β垂直吗?
(2)什么情况下α里的直线和β垂直?
思考3 垂足为B,那么直线AB与平面β的位置关系如何? 为什么?
∵ , ∴AB⊥BE.
又由题意知AB⊥CD,且BE CD=B
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
(线是一个平面内垂直于两平面交线的一条直线)
作用: ①它能判定线面垂直. ② 它能在一个平面内作与这个平面垂 直的垂线.
思考4 设平面 ⊥ 平面 ,点P在平面 内,过点P作平面 的垂线a,直线a与平面 具有什么位置关系?
直线a在平面 内
在γ内过A点作直线 a ⊥n,
在γ内过A点作直线 b⊥m,
在γ内任取一点A(不在m,n上),
如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.
判断线面垂直的两种方法:①线线垂直→线面垂直;②面面垂直→线面垂直.
例题1 如图4,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在平面,D、E分别是VA、VC的中点,直线 DE与平面VBC有什么关系?试说明理由.
解:由VC垂直于⊙O所在平面,知VC⊥AC,VC⊥BC,即 ∠ACB是二面角A-VC-B的平面角.由∠ACB是直径上的圆周角,知 ∠ACB =90°。
因此,平面 VAC⊥平面VBC.由DE是△VAC两边中点连线,知 DE∥AC,故DE⊥VC.由两个平面垂直的性质定理,知直线DE与平面VBC垂直。
注意:本题也可以先推出AC垂直于平面VBC,再由DE∥AC,推出上面的结论。
例2.S为三角形ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC。 求证:AB⊥BC。
证明:过A点作AD⊥SB于D点.∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC,∴ AD⊥BC.
又∵ SA ⊥ 平面ABC, ∴SA ⊥ BC. AD∩SA=A∴BC ⊥ 平面SAB.∴BC ⊥AB.
练习1:如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。
2.如图,平面AED ⊥平面ABCD,△AED是等边三角形,四边形ABCD是矩形,
(1)求证:EA⊥CD
(2)若AD=1,AB= ,求EC与平面ABCD所成的角。
(2012·北京模拟)如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(1)求证:BM∥平面ADEF;(2)求证:平面BDE⊥平面BEC.
证明:(1)取DE中点N,连接MN,AN.在△EDC中,M,N分别为EC,ED的中点,所以MN//CD,且MN= CD.由已知AB//CD,AB= CD,所以MN//AB,且MN=AB,所以四边形ABMN为平行四边形.所以BM//AN.又因为AN平面ADEF,且BM 平面ADEF,所以BM//平面ADEF.
(2)因为四边形ADEF为正方形,所以ED⊥AD,又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD.又因为EDB 平面ADEF,所以ED⊥平面ABCD.所以ED⊥BC.
在直角梯形ABCD中,AB=AD=2,CD=4,可得BC= ,在△BCD中,BD=BC= ,CD=4,所以BC⊥BD,BD∩ED=D,所以BC⊥平面BDE,又因为BC 平面BCE,所以平面BDE⊥平面BEC.
(4)已知面面垂直易找面的垂线,且在某一个平面内
(5) 解题过程中应注意充分领悟、应用
(3) 证明面面垂直要从寻找面的垂线入手
(2) 理解面面垂直的判定与性质都要依赖面面垂直的定义
(1) 定义面面垂直是在建立在二面角的定义的基础上的
2.面面垂直的性质推论:
1.平面与平面垂直的性质定理:














