




北师大版 (2019)必修 第二册第六章 立体几何初步5 垂直关系本节综合与测试教课内容课件ppt
展开空间两条直线的位置关系垂直异面平行
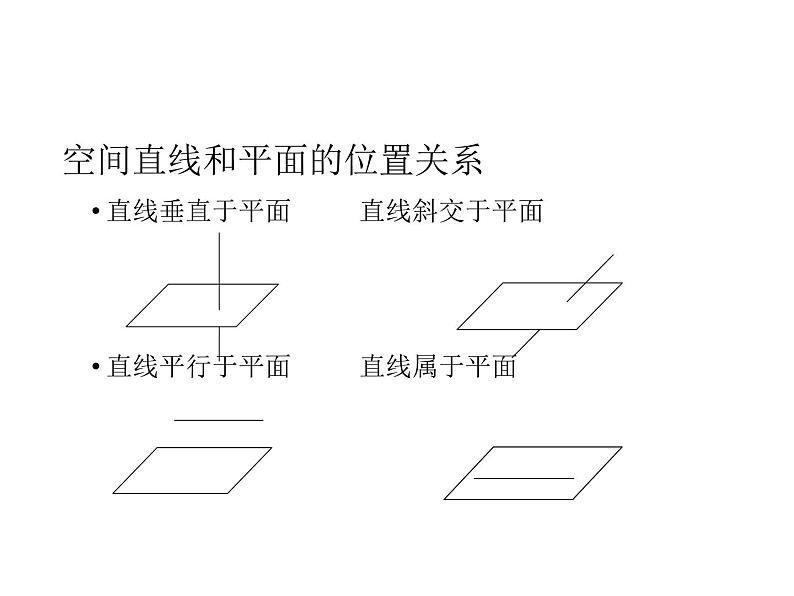
空间直线和平面的位置关系直线垂直于平面直线斜交于平面直线平行于平面直线属于平面
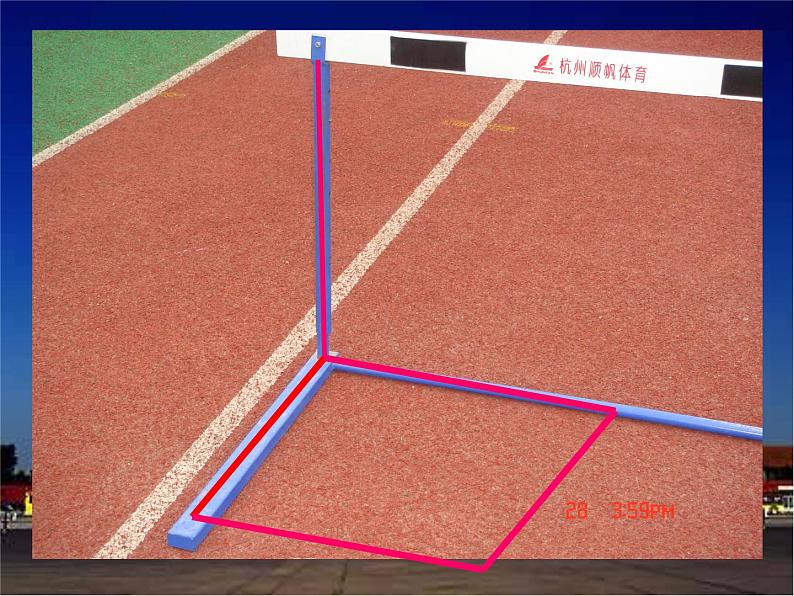
生活中的垂直生活中的垂直
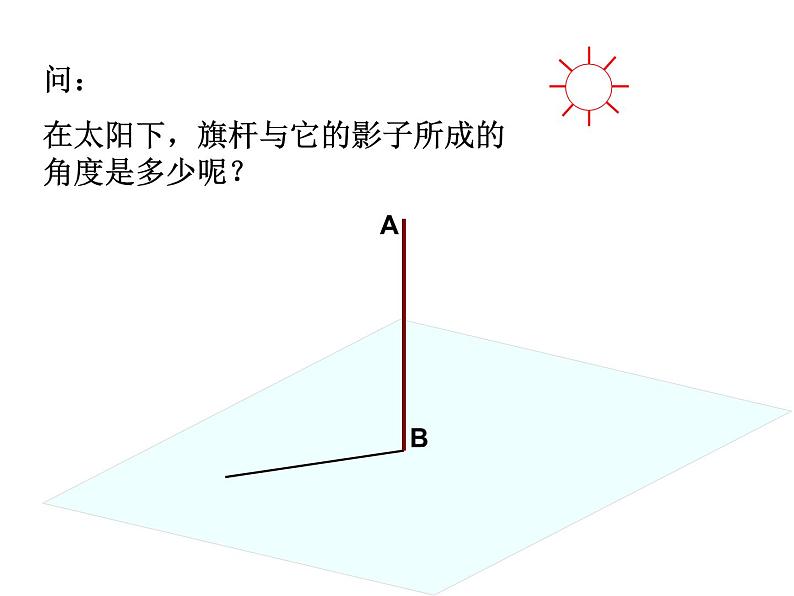
问:在太阳下,旗杆与它的影子所成的角度是多少呢?
随着时间的变化,影子的位置移动,而旗杆与影子所成的角度是否发生改变呢?
问:旗杆和地面上其他直线的关系又如何呢?
直线与平面垂直的定义:
直线叫做平面的垂线,平面叫做直线的垂面,交点叫做垂足.
二、直线与平面垂直的画法二、直线与平面垂直的画法
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示.
直线与平面的一条边垂直
思考:(1)过空间一点作已知平面的垂线有几条? (2)过空间一点作已知直线的垂面有几个?
⑴:过一点有且只有一条直线和一个平面垂直.
⑵:过一点有且只有一个平面和一条直线垂直.
例: 求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
除定义外,如何判定一条直线与平面垂直呢?
如图,准备一块三角形的纸片,做一个试验:
过 的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)
如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
三、直线与平面垂直判定定理6.1:
记忆:线线垂直,则线面垂直
2. 如果一条直线和一个平面内的无数条直线都垂直,则直线与此平面垂直
3. 如果一条直线和一个平面内的任何两条直线都垂直,则直线与此平面垂直
判断下列命题是否正确?
1、如图,空间中直线l和三角形的两边AC,BC同时垂直,则这条直线和三角形的第三边AB的位置关系是( )A. 平行B. 垂直C. 相交D. 不确定
(1)平行于同一直线的两条直线互相平行;
(2)垂直于同一直线的两条直线互相平行;
(3)平行于同一平面的两条直线互相平行;
(4)垂直于同一平面的两条直线互相平行。
A.(1)(3)(4) B.(1)(4) C.(1) D.都正确
例1:如图,点P 是平行四边形ABCD 所在平面外一点,O 是对角线AC与BD的交点,且PA =PC ,PB =PD .求证:PO⊥平面ABCD
归纳: 1.要证明线线垂直,往往转化为证明线面垂直,然后用线面垂直的基本性质. 2.要证明线面垂直,只要在该平面内找到两条相交直线与已知直线垂直就行.
问题1:平面几何中“角”是怎样定义的?
问题2:在立体几何中,“异面直线所成的角”、“直线和平面所成的角”有什么共同的特征?
有公共顶点的两条射线所形成的图形
问题3:在生产实践中,有许多问题要涉及两个平面相交所成的角的情形,你能举出这个问题的一些例子吗?
这样的角有何特点,该如何表示呢?请进入本节课的学习!
堤坝面与河底水平面,打开的笔记本电脑
从一条直线出发的两个半平面所组成的图形叫作二面角,
这条直线叫作二面角的棱,这两个半平面叫作二面角的面.
半平面:一个平面内的一条直线,把这个平面分成_______,其中的_________都叫作半平面.
二面角- l-
从一点出发的两条射线所组成的图形叫作角.
边—点—边 (顶点)
从一条直线出发的两个半平面所组成的图形叫作二面角.
面—直线—面 (棱)
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角.
二面角的平面角必须满足:
二面角的大小用它的平面角的大小来度量
∠APB= ∠A1P1B1
二面角的平面角的范围: 0180.
两个平面相交,如果它们所成的二面角是直二面角,则两个平面垂直.
1. 凡是直二面角都相等;
2. 两个平面相交,可引出四个二面角,如果其中有一个是直二面角,那么其他各个二面角都是直二面角.
问题1:根据定义判断两个平面是否垂直需要解决什么问题?提示:两个平面所成的角是否为直二面角
问题2:如图,∠AOB为直二面角α-l-β的平面角,那么直线AO与平面α的位置关系如何?
探究点3 平面与平面垂直的判定
两个平面垂直的判定定理:
定理6.2:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
注:这个定理简称“线面垂直,则面面垂直.”
分析:作出它的一个平面角,并证明这个平面角是直角.如何作平面角呢?可以作BE⊥CD,使∠ABE为二面角α-CD-β的平面角.
证明:设a∩β=CD,则B∈CD.
在平面β内过点B作直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角,又AB⊥BE,即二面角α-CD-β是直二面角.
两个平面垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出一个平面垂直于另一个平面的依据.
如:建筑工人砌墙时,沿系有铅锤的线砌墙
例:如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,C为⊙O上异于A,B的一点.求证:平面PAC⊥平面PBC.
证明:设⊙O所在平面为α,由已知条件,有PA⊥α,BC在α内,所以,PA⊥BC.因为,点C是不同于A,B的任意一点,AB为⊙O的直径,所以,∠BCA=90°,即BC⊥CA.又因为PA与AC是△PAC所在平面内的两条相交直线,所以,BC⊥平面PAC,又因为BC在平面PBC内,所以,平面PAC⊥平面PBC.
思考:你还能发现哪些面互相垂直?
1.二面角指的是( )A.从一条直线出发的两个半平面所夹的角度B.从一条直线出发的两个半平面所组成的图形C.两个平面相交时,两个平面所夹的锐角D.过棱上一点和棱垂直的两条射线所成的角
3.直三棱柱ABC-A′B′C′中,底面三角形ABC为正三角形,则两侧面AA′C′C与AA′B′B所成二面角的大小为_______.
1.二面角的定义及度量.
2.判断两个平面垂直的方法.①定义法②根据面面垂直的判定定理3.从面面垂直的判定定理我们还可以看出面面垂直的问题可以转化为线面垂直的问题来解决.
图中立柱与地面是垂直的,你能得出什么结论?
国旗与地面都是垂直的,你能发现什么现象?
问题1.如图,长方体ABCD—A1B1C1D1中,棱AA1,BB1,CC1,DD1所在直线与底面ABCD的位置关系如何?它们彼此之间具有什么位置关系?
问题2.一个平面的垂线有多少条?这些直线彼此之间具有什么位置关系?
问题3:如果直线a,b都垂直于平面α,由观察可知a//b,从理论上如何证明这个结论?
线面垂直、面面垂直的性质
经过同一点 的两直线 , 都垂直于 是不可能的,所以
证明:假定 不平行,设 ,经过点作直线 与直线 平行
直线与平面垂直的性质定理
定理6.3 如果两条直线同垂直于一个平面,那么这两条直线平行
1.设a,b为直线,α为平面,若a⊥α,b//a,则b与α的位置关系如何?
2.设l为直线,α,β为平面,若l⊥α,α//β,则l与β的位置关系如何?
3.设l为直线,α、β为平面,若l⊥α,l⊥β,则平面α、β的位置关系如何?
例2、正方体ABCD-A1B1C1D1中,EF与异面直线AC、A1D都垂直且相 交,分别交AC、A1D于E、F 求证:EF∥BD1
证明:连接A1C1、C1D、B1D1、AD1
∵AC∥A1C1 且EF⊥AC∴EF⊥A1C1又EF⊥A1D ∴EF⊥平面A1C1D∵AB⊥A1D 且AD1⊥A1D∴A1D⊥平面ABD1∴BD1⊥A1D 同理可证BD1⊥A1C1∴BD1⊥平面A1C1D∴EF∥BD1
墙壁与地面是垂直的,你有什么发现?请进入本节课的学习!
1.掌握平面与平面垂直的性质定理,并能用文字、符号和图形语言描述定理.(重点)2.能够灵活地应用面面垂直的性质定理证明有关问题.(难点)3.通过定理的学习,培养空间想象能力、推理论证能力、几何直观能力.(难点)
平面与平面垂直的性质定理
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
如何用符号语言描述这个定理?
问题1:若α⊥β,过平面α内一点A作平面β的垂线,垂足为B,那么点B在什么位置?说明你的理由.
平面与平面垂直的性质的应用
问题2:如果两个平面互相垂直,那么经过一个平面内一点且垂直于另一个平面的直线,此直线与该平面是何位置关系?
问题3:对于三个平面α,β,γ,如果α⊥γ,β⊥γ, ,那么直线l与平面γ的位置关系如何?为什么?
已知:三个平面求证:
例2:如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,求证:BC⊥AB
证明:过点A作AE⊥PB垂足为E∵平面PAB⊥平面PBC, 平面PAB∩平面PBC=PB,∴AE⊥平面PBC∵BC 平面PBC ∴AE⊥BC
∵PA⊥平面ABC,BC 平面ABC∴PA⊥BC
AB 平面ABC∴ AB ⊥BC
【提升总结】线线垂直、线面垂直、面面垂直的关系
1.判断题:(1)两个平面垂直,经过一个平面内的一点与交线垂直的直线垂直于另一个平面. ( )(2)三个平面α,β,γ,若α⊥β,β⊥γ,那么α∥γ. ( )(3)三个平面α,β,γ,若α∥β,γ⊥α,那么γ⊥β. ( )
(4)过平面外的一条直线只可以作一平面垂直于这个平面. ( )
北师大版 (2019)必修 第二册1.2 向量的基本关系教课ppt课件: 这是一份北师大版 (2019)必修 第二册1.2 向量的基本关系教课ppt课件,共27页。PPT课件主要包含了相等向量,共线向量,忽视零向量致误,对共线向量理解错误等内容,欢迎下载使用。
北师大版 (2019)必修 第二册第一章 三角函数7 正切函数本节综合与测试课文配套ppt课件: 这是一份北师大版 (2019)必修 第二册第一章 三角函数7 正切函数本节综合与测试课文配套ppt课件,共1页。
2020-2021学年第六章 立体几何初步4 平行关系本节综合与测试多媒体教学ppt课件: 这是一份2020-2021学年第六章 立体几何初步4 平行关系本节综合与测试多媒体教学ppt课件,共60页。PPT课件主要包含了平行关系的判定,线线平行,线面平行,观察与猜想,直线与平面平行的画法,反思领悟,线不在多重在相交,符号表示,图形表示,结论结论等内容,欢迎下载使用。













