






《导数的概念》人教版高中数学选修2-2PPT课件(第1.1.2课时)
展开平均速度不能反映物体在某段时间里的运动状态,那么用什么来衡量物体的状态呢?
如何知道运动员在每一时刻的速度呢?
汽车在每一刻的速度怎么知道呢?
在高台跳水运动中,运动员在不同时刻的速度是不同的.我们把物体在某一时刻的速度称为瞬时速度(instaneus velciy).
平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也即需要通过瞬时速度来反映.
瞬时速度与平均速度的区别
已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t表示时间),求物体在t0 时刻的速度.
物体的运动规律是 s=s(t),那么物体在时刻 t 的瞬时速度v,就是物体在t到 t+Δt这段时间内,当 Δt-0 时的平均速度:
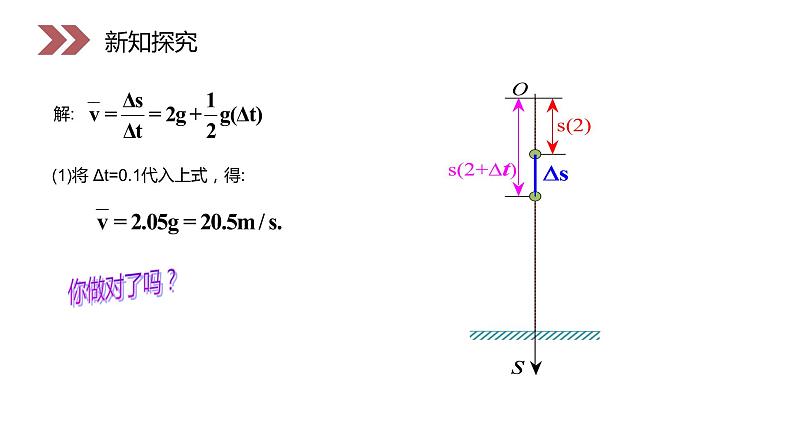
物体作自由落体运动,运动方程为: 其中位移单位是m,时间单位是s,g=10m/s2.求:(1) 物体在时间区间[2,2.1]上的平均速度;(2) 物体在t=2(s)时的瞬时速度.
即物体在时刻t0=2(s)的瞬时速度等于20(m/s).当时间间隔Δt 逐渐变小时,平均速度就越接近t0=2(s) 时的瞬时速度v=20(m/s).
从而平均速度 的极限为
还记得上节课讲的关于高台跳水问题吗?运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系:
通过列表看出平均速度的变化趋势 :
知道了瞬时速度的概念,那么在高台跳水运动中,如何求(比如,t=2)运动员的瞬时速度?
△t<0时,在[2+ △t,2]这段时间内
△t>0时,在[2,2+ △t]这段时间内
我们用 表示 “当t=2, Δt趋近于0 时,平均速度趋于确定值-13.1”.
那么运动员在某一时刻t0的瞬时速度怎么表示?
函数y=f(x)在x=x0处的瞬时变化率又怎么表示?
一般将导数记作 ,或 者 ,即
表示函数y关于自变量x在 处的导数
f(x)在点x0处可导
f(x)在点x0处的导数
是函数f(x)在以x0与x0+Δx 为端点的区间[x0,x0+Δx](或[x0+Δx,x0])上的平均变化率,而导数则是函数f (x)在点x0 处的变化率,它反映了函数随自变量变化而变化的快慢程度.
事实上,导数也可以用下式表示:
如果函数y=f(x)在点x=x0存在导数,就说函数y=f(x)在点x0处可导,如果极限不存在,就说函数 f(x)在点x0处不可导.
由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:
这里的增量不是一般意义上的增量,它可正也可负.自变量的增量Δx的形式是多样的,但不论Δx选择哪种形式, Δy也必须选择与之相对应的形式
求函数y=x2在x=1处的导数.
求函数y=x+1/x在x=2处的导数.
设函数f(x)在点x0处可导,求下列极限值.
说明在第3h附近,原油的温度大约以1℃/h的速率下降,原油温度以大约以3℃/h的速率上升.
物体在某一时刻的速度称为瞬时速度.
高中数学人教版新课标A选修2-21.3导数在研究函数中的应用教学ppt课件: 这是一份高中数学人教版新课标A选修2-21.3导数在研究函数中的应用教学ppt课件,共28页。PPT课件主要包含了课前导入,直角坐标系,平面图形的面积,新知探究,因此平面图形的面积为,面积为,解方程组,得交点的横坐标,曲边扇形面积元素,曲边扇形的面积公式等内容,欢迎下载使用。
高中数学人教版新课标A选修2-21.2导数的计算课文ppt课件: 这是一份高中数学人教版新课标A选修2-21.2导数的计算课文ppt课件,共29页。PPT课件主要包含了课前导入,观察下图中的曲线,新知探究,极大值的概念,极小值的概念,你知道吗,下面分两种情况讨论,例题讲解,你还能再举例吗,课堂练习等内容,欢迎下载使用。
高中数学人教版新课标A选修2-21.3导数在研究函数中的应用教课课件ppt: 这是一份高中数学人教版新课标A选修2-21.3导数在研究函数中的应用教课课件ppt,共26页。PPT课件主要包含了课前导入,导数的几何意义,1求增量,2算比值,3求极限,求函数的导数的方法,导数的计算,常见函数导数,导数运算法则,本节知识结构等内容,欢迎下载使用。













