七年级下册5.2.1 平行线课后作业题

这是一份七年级下册5.2.1 平行线课后作业题，共55页。
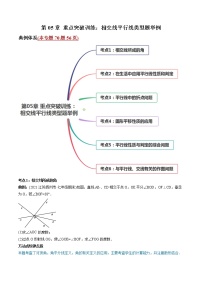
第05章 重点突破训练：相交线平行线类型题举例
典例体系(本专题70题56页)

考点1：相交线所成的角
典例：(2021·江苏扬州市·七年级期末)如图，直线AB、CD相交于点O，OE平分∠BOD，OF⊥CD，垂足为O，若∠BOF=38°．

(1)求∠AOC的度数；
(2)过点O作射线OG，使∠GOE=∠BOF，求∠FOG的度数．
【答案】(1)52°；(2)图见解析，26°或102°
【详解】
(1)∵OF⊥CD，∠BOF＝38°，
∴∠BOD＝90°−38°＝52°，
∴∠AOC＝52°；
(2)由(1)知：∠BOD＝52°，
∵OE平分∠BOD，
∴∠BOE=26°，
此时∠GOE=∠BOF=38°，
分两种情况：
如图：

此时∠FOG=∠BOF+∠BOE-∠GOE=38°+26°-38°=26°；
如图：

此时∠FOG=∠BOF+∠BOE+∠GOE=38°+26°+38°=102°；
综上：∠FOG的度数为26°或102°.
方法或规律点拨
本题考查了对顶角，角平分线定义，角的有关定义的应用，主要考查学生的计算能力，并注意数形结合．
巩固练习
1．(2021·山东济南市·七年级期末)如图，直线m和n相交于点O，若∠1=40°，则∠2的度数是(　　　)

A．40° B．50° C．140° D．150°
【答案】C
【详解】解：直线m和n相交于点O，若∠1=40°，则∠2的度数为180°-∠1= 140°，
故选：C．
2．(2021·湖北随州市·七年级期末)如图，直线，交于点，射线平分，如果，那么等于( )

A．38° B．37° C．36° D．52°
【答案】A
【详解】解：∵
∴∠AOC =180°−104°=76°
∵OM 平分∠AOC
∴∠MOC=

=38°
故选：A
3．(2021·广西桂林市·七年级期末)按语句画图：点在直线上，也在直线上，但不在直线上，直线，，两两相交正确的是(　　　)
A．B．C．D．
【答案】A
【详解】解：A．符合条件，
B．不符合点P不在直线c上；
C．不符合点P在直线a上；
D．不符合直线a、b、c两两相交；
故选：A．
4．(2021·浙江温州市·七年级期末)如图，直线AB，CD相交于点O，AO平分，且，则的度数是________．

【答案】
【详解】∵，，
∴，
∵AO平分，
∴,
∴∠DOB=,
故答案为：．
5．(2021·浙江温州市·七年级期末)如图，直线AB与直线CD相交于点O，射线OE在内部，OA平分．
(1)当时，写出图中所有与互补的角．
(2)当时，求的度数．

【答案】(1)、、；(2)36°．
【详解】解：(1)∵，
∴，
∵OA平分，
∴，
∴，
∴，
∴与互补的角有、、；
(2)根据题意，
∵，
又∵，
∴，
∵OA平分，
∴，
∴；
6．(2021·浙江湖州市·七年级期末)如图，已知直线与相交于点为的角平分线．
(1)求的度数；
(2)求的度数．

【答案】(1)；(2)
【详解】解：(1)，
∴，
∵，
；
(2)∵直线与相交于点O，
，
∴，
为的角平分线，
，
．
7．(2021·浙江宁波市·七年级期末)如图，已知直线，相交于点，平分，平分．若，
求：(1)的度数；
(2)的度数．

【答案】(1)40°；(2)150°
【详解】(1)∵直线，相交于点，
∴，
∵，
∴，
∵平分，
∴．
(2)∵，
∴，
∵平分，
∴，
∵，
∴．
7．(2021·重庆长寿区·七年级期末)如图，直线、相交于点，平分，平分，．
(1)求的度数；
(2)求的度数．

【答案】(1)30°，(2)45°．
【详解】
解：(1)∵，∠AOD+∠BOD＝180°，
∴∠BOD＝×180°＝60°，
∵OE平分∠BOD，
∴∠DOE＝∠BOE=∠BOD＝×60°＝30°；
(2)∠COE＝∠COD﹣∠DOE＝180°﹣30°＝150°，
∵OF平分∠COE，
∴∠EOF＝∠COE＝×150°＝75°，
由(1)得，∠BOE＝30°，
∴∠BOF＝∠EOF-∠BOE＝75°-30°＝45°．
8．(2021·四川宜宾市·七年级期末)如图，点是直线上的一点，，平分，于点．

(1)求的度数；
(2)试说明平分．
【答案】(1)；(2)见解析
【详解】(1)解：∵，
∴，
∵，
∴，
∴；
(2)证明：∵，，
∴，
∵，平分，
∴，
∵，
∴，
∴，
∵，
∴，
∴平分．
9．(2021·湖北鄂州市·七年级期末)如图，点在直线上，与互补，平分．

(1)若，则的度数为 ；
(2)若，求的度数．
【答案】(1)15°；(2)76°
【详解】解：(1)点在直线上，，
，
与互补，
，
平分，
，
；
故答案为：；
(2)点在直线上，
与互补，
与互补，
，
平分，
，
设为，可得：，
解得：，
．
10．(2021·江苏泰州市·七年级期末)如图，已知直线，相交于点，与互余．
(1)若，求的度数；
(2)若，求的度数．

【答案】(1)58°；(2)120°
【详解】解(1)因为与是对顶角，
所以，
因为与互余，
所以，
所以

；
(2)因为，
所以，
因为，
所以，
，
又，
，
所以

．
11．(2021·广东东莞市·七年级期末)如图为直线上一点，，平分，．

(1)求的度数；
(2)试判断是否平分，并说明理由；
(3)的余角是 ．
【答案】(1)155°；(2)平分，理由见解析；(3)和
【详解】解：(1)因为，平分，
所以，
所以．
(2)平分．理由如下：
因为，，
所以，
由(1)得∠BOD=155°，
所以，
所以，
所以平分．
(3)因为，∠COD=∠AOD，∠COE+∠COD=90°，
所以∠BOE+∠COD=90°，∠BOE+∠AOD=90°，
所以的余角是和．
考点2：在生活中应用平行线性质和判定
典例：(2020·江苏泰兴市实验初级中学七年级月考)某段铁路两旁安置了两座可旋转探照灯，主道路是平行，即PQ∥MN． 如图所示，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是每秒2度，灯B转动的速度是每秒1度． 若灯B射线先转动30秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动_________秒，两灯的光束互相平行．

【答案】30或110
【详解】解：设灯转动t秒，两灯的光束互相平行，即AC∥BD，
①当0＜t≤90时，如图1所示：
∵PQ∥MN，则∠PBD＝∠BDA，
∵AC∥BD，则∠CAM＝∠BDA，
∴∠PBD＝∠CAM
有题意可知：2t＝30＋t
解得：t＝30，

②当90＜t＜150时，如图2所示：
∵PQ∥MN，则∠PBD＋∠BDA＝180°，
∵AC∥BD，则∠CAN＝∠BDA，
∴∠PBD＋∠CAN＝180°，
∴30＋t＋(2t－180)＝180
解得：t＝110

综上所述，当t＝30秒或t＝110秒时，两灯的光束互相平行．
故答案为：30或110
方法或规律点拨
本题主要考查补角、角的运算、平行线的性质的应用，解题的关键是熟练掌握平行线的性质，注意分两种情况谈论．
巩固练习
1．(2021·山西朔州市·七年级期末)一艘船停留在海面上，如果从船上看灯塔位于北偏东30°，那么从灯塔看船上位于灯塔的( )
A．北偏东30° B．北偏东60° C．南偏西30° D．南偏西60°
【答案】C
【详解】解：设此船位于海面上的C处，灯塔位于D处，
射线CA、DB的方向分别为正北方向与正南方向，如图所示．
∵从船上看灯塔位于北偏东30°，
∴∠ACD=30°．
又∵AC∥BD，∴∠CDB=∠ACD=30°．
即从灯塔看船位于灯塔的南偏西30°．
故选：C．

2．(2021·甘肃白银市·七年级期末)一条船停留在海面上，从船上看灯塔位于北偏东60°方向，那么从灯塔看船位于灯塔的 方向(　　)
A．南偏西60° B．西偏南60° C．南偏西30° D．北偏西30°
【答案】A
【详解】
解：设此船位于海面上的C处，灯塔位于D处，射线CA、DB的方向分别为正北方向与正南方向，如图所示：

∵从船上看灯塔位于北偏东60°，
∴∠ACD＝60°．
又∵AC∥BD，
∴∠CDB＝∠ACD＝60°．
即从灯塔看船位于灯塔的南偏西60°．
故选：A．
3．(2020·重庆璧山区·八年级期中)如图是长方形纸带，，将纸带沿折叠成图，再沿折叠成图，则图中的的度数是( )

A．102° B．112° C．120° D．128°
【答案】A
【详解】解：∵AD∥BC，∠DEF=26°，
∴∠BFE=∠DEF=26°，
∴∠EFC=154°(图a)，
∴∠BFC=154°-26°=128°(图b)，
∴∠CFE=128°-26°=102°(图c)．
故选：A．
4．(2019·山西九年级专题练习)某同学在研究传统文化“抖空竹”时有一个发现：他把它抽象成数学问题，如图所示：已知，，，则的度数是( )

A． B． C． D．
【答案】B
【详解】解：如图，

延长交于，
，，
，
又，
，
故选．
5．(2020·河南省实验中学)如图，一条公路修到湖边时，需拐弯绕道而过，如果第一次拐的角∠A＝120°，第二次拐的角∠B＝160°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C 是( )

A．120° B．130° C．140° D．150°
【答案】C
【详解】根据平行线的性质可得

故答案为：C．
6．(2019·山西七年级月考)小林乘车进入车库时仔细观察了车库门口的“曲臂直杆道闸”，并抽象出如图所示的模型，已知垂直于水平地面．当车牌被自动识别后，曲臂直杆道闸的段绕点缓慢向上旋转，段则一直保持水平状态上升(即与始终平行)，在该过程中始终等于( )

A． B． C． D．
【答案】D
【详解】解：过点B作BG∥CD

由题意可知：CD∥AE，∠BAE=90°
∴BG∥CD∥AE
∴∠ABG=180°－∠BAE=90°，=180°
∴=∠ABG＋=270°
故选D．
7．(2021·陕西西安市·八年级期末)一大门的栏杆如图所示，BA垂直地面AE于点A，CD平行于地面AE，则∠ABC＋∠BCD＝_____．

【答案】270°
【详解】过B作BF∥AE，
∵CD∥ AE，
则CD∥BF∥AE，

∴∠BCD+∠1=180°，
又∵AB⊥AE，
∴AB⊥BF，
∴∠ABF=90°，
∴∠ABC+∠BCD=90°+180°=270°．
故答案为：270．
8．(2021·山东潍坊市·八年级期末)光线在不同介质中传播速度不同，从一种介质斜射进入另一种介质时会发生折射．如图，水面与水杯下沿平行，光线从水中射向空气时发生折射，光线变成，点在射线上，已知，则的度数是_______．

【答案】
【详解】解：∵AB∥CD，
∴∠GFB=∠FED=45°．
∵∠HFB=20°，
∴∠GFH=∠GFB-∠HFB=45°-20°=25°．
故答案为：25°
9．(2021·全国七年级)如图，在甲，乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东，若同时开工，则在乙地公路按南偏西___度的走向施工，才能使公路准确接通．

【答案】55
【详解】解：如图：

，
，
即在乙地公路应按南偏西55度的走向施工，才能使公路准确接通．
故答案为：55．
10．(2018·太原师范学院附属中学七年级月考)如图，要修建一条公路，从村沿北偏东75°方向到村，从村沿北偏西25°方向到村．若要保持公路与的方向一致，则的度数为______．

【答案】80°
【详解】由题意可得：AN∥FB，EC∥BD，
故∠NAB=∠FBD=75°，
∵∠CBF=25°，
∴∠CBD=100°，
则∠ECB=180°-100°=80°．
故答案为：80°．

11．(2014·陕西九年级专题练习)如图，∠AOB的两边OA、OB均为平面反光镜，∠AOB＝40°，在射线OB上有一点P，从点P点射出的一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是___________

【答案】80°
【解析】
已知反射光线QR恰好与OB平行，根据平行线的性质可得∠AOB＝∠AQR＝40°，根据平角的定义可得∠PQR＝100°，再由两直线平行，同旁内角互补互补可得∠QPB=80°.
12．(2021·全国七年级)如图，在、两处之间要修一条笔直的公路，从地测得公路走向是北偏东，公司要求、两地同时开工，并保证若干天后公路准确接通．
(1)地修公路的走向应该是　　 ；
(2)若公路长12千米，另一条公路长6千米，且的走向是北偏西，试求到公路的距离？

【答案】(1)地所修公路的走向是南偏西；(2)12km
【详解】
(1)由两地南北方向平行，根据内错角相等，可知地所修公路的走向是南偏西．
故答案为：南偏西．
(2)，
，
地到公路的距离是千米．
13．(2020·山东临沂市·七年级期末)如图，点是内部一点，交于点．请你画出射线，并且，或的反向延长线交于点．
(1)补全图形；
(2)判断与的数量关系，并证明．

【答案】(1)见解析；(2)∠AOB与∠MPN相等或互补；证明见解析．
【详解】解：(1)

(2)∠AOB与∠MPN相等或互补．
证明：如图1，∵PM∥OA，
∴∠AOB＝∠PCB，
∵PN∥OB，
∴∠MPN＝∠PCB，
∴∠AOB＝∠MPN；
如图2，∵PM∥OA，
∴∠AOB＝∠PCB，
∵PN∥OB，
∴∠MPN+∠PCB＝180°，
∴∠AOB+∠MPN＝180°．
综上所述，∠AOB与∠MPN相等或互补．
14．(2020·银川九中英才学校七年级期中)如图是种躺椅及其简化结构示意图，扶手与底座都平行于地面，靠背与支架平行，前支架与后支架分别与交于点和点与交于点，当时，人躺着最舒服，求此时扶手与支架的夹角和扶手与靠背的夹角的度数．

【答案】∠AOE=60°，∠ANM=120°
【详解】
∵扶手AB与底座CD都平行于地面，
∴AB∥CD，
∴∠ODC=∠BOD=30°，
又∵∠EOF=90°，
∴∠AOE=60°，
∵DM∥OE，
∴∠AND=∠AOE=60°，
∴∠ANM=180°-∠AND=120°．
考点3：平行线中的折点问题
典例：(2020·宁波市惠贞书院七年级期中)如图，，设，那么，，的关系式______．

【答案】
【详解】如图，过作，过作，
∴，
∴，，，
∵，
∴，
∴，
∴，
∴，
∴．
故答案为：．

方法或规律点拨
本题考查了平行线的性质，两直线平行同位角相等，两直线平行内错角相等，正确理解平行线的性质是解题的关键；
1．(2021·渝中区·重庆巴蜀中学七年级期末)如图，，，，则( )

A． B． C． D．
【答案】D
【详解】
如图，过点E作，

，
，
又，
，
，
，
故选：D．
2．(2020·四川攀枝花市·七年级期末)如图，某地域的江水经过B、C、D三点处拐弯后，水流的方向与原来相同，若∠ABC＝125°，∠BCD＝75°，则∠CDE的度数为( )

A．20° B．25° C．35° D．50°
【答案】A
【详解】解：由题意得，AB∥DE，
如图，过点C作CF∥AB，则CF∥DE，

∴∠BCF+∠ABC=180°，
∴∠BCF=180°-125°=55°，
∴∠DCF=75°-55°=20°，
∴∠CDE=∠DCF=20°．
故选：A．
3．(2020·浙江杭州市·七年级其他模拟)如图：，，，的度数为( )

A． B． C． D．
【答案】D
【详解】如图，过点C作，
，
，
，
，
，
，
故选：D．

4．(2020·重庆市万州第二高级中学九年级期中)如图，直线为直角，则等于( )

A． B． C． D．
【答案】B
【详解】解：过E作EF∥AB，

∵AB∥CD，
∴AB∥CD∥EF．
∴∠C＝∠FEC，∠BAE＝∠FEA．
∵∠C＝40°，∠AEC为直角，
∴∠FEC＝40°，∠BAE＝∠AEF＝90°−40°＝50°．
∴∠1＝180°−∠BAE＝180°−50°＝130°．
故选：B．
5．(2021·全国七年级)如图，已知，，，则____________

【答案】
【详解】解：作直线m∥a，n∥b，如图所示：

∵，
∴，
∴∠1=∠5，∠6=∠7，∠8=∠4，
∴∠2-∠5=∠6，∠3-∠8=∠7，
∴，
，
则有，
；
故答案为45°．
6．(2020·上海市民办立达中学七年级月考)如图，AB//CD，则图中_______________°；

【答案】180
【详解】如图：过点E作EF//CD．
∴∠3＝∠FEC
∵∠AEF＋∠2＝∠FEC，
∴∠2＋∠AEF＝∠3，
∴，
∵AB//CD，EF//CD，
∴EF//AB，
∴∠1＋∠AEF＝180°
∴．

故答案为：180°
7．(2021·全国九年级)如图，AEFC是折线，AB//CD，那么∠1，∠2，∠3，∠4的大小所满足的关系式为_______________；

【答案】或
【详解】解：过点作，过点作，
，
，
，，，
，，
或．
故答案为：或．

考点4：图形平移性质的应用
典例：(2020·河南郑州市·郑州外国语中学七年级期中)如图，在中，，把沿着直线BC的方向平移后得到，连接AE，AD，有以下结论：①；②；③；④.其中正确的结论有( )

A．1个 B．2个 C．3个 D．4个
【答案】D
【详解】∵△ABC沿着直线BC的方向平移后得到△DEF，
∴AB//DE，AC//DF，AD//CF，CF=AD=2.5cm，故①②③正确.
∵∠BAC=90°，
∴AB⊥AC，
∵AB//DE
，故④正确.
综上所述：之前的结论有：①②③④，共4个，
故选D.
方法或规律点拨
本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．
巩固练习
1．(2020·河北石家庄市·九年级其他模拟) 某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是( )

A．甲种方案所用铁丝最长 B．乙种方案所用铁丝最长
C．丙种方案所用铁丝最长 D．三种方案所用铁丝一样长:学*科*网]
【答案】D
【解析】解：由图形可得出：甲所用铁丝的长度为：2a+2b，
乙所用铁丝的长度为：2a+2b，
丙所用铁丝的长度为：2a+2b，
故三种方案所用铁丝一样长．
故选D．
2．(2019·浙江台州市·七年级期末)三个边长分别为，，，的正方形如图所示摆放，则阴影部分的周长( )

A．只与，有关 B．只与，有关 C．只与，有关 D．与，，有关
【答案】B
【详解】
解：阴影部分的周长：
故选：B．
3．(2021·全国七年级)如图，长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等，且每段小路均为平行四边形)，小路进出口的宽度均为1米，则绿地的面积为__平方米．

【答案】42
【详解】解：由平移的性质，得:
草坪的长为8﹣1＝7(米)，宽为6米，
草坪的面积＝7×6＝42(平方米)．
故答案为：42．
4．(2020·忠县乌杨初级中学校七年级月考)如图,在长方形草地内修建了宽为2米的道路,则草地面积为_______米2．

【答案】144
【详解】解：由图形得到了的总长度为20+10-2=28米，
所以道路的总面积为28×2=56米2，
所以草地面积为20×10-56=144米2．
故答案为：144
5．(2020·江苏扬州市·七年级期末)如图是某公园里一处矩形风景欣赏区ABCD，长AB=50米，宽BC=30米，为方便游人观赏，公园特意修建了如图所示的小路(图中非阴影部分)，小路的宽均为1米，那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为______米．

【答案】98
【解析】∵利用已知可以得出此图形可以分为横向与纵向分析，水平距离等于AB，铅直距离等于(AD-1)×2，
又∵长AB=50米，宽BC=25米，
∴小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为50+(25-1)×2=98米，
故答案为98．
6．(2020·莆田擢英中学七年级月考)如图是一块从一个边长为50 cm的正方形材料中剪出的垫片，现测得FG＝5 cm，则这个剪出的垫片的周长是________cm.

【答案】210
【解析】
【详解】如图所示：这块垫片的周长为：50×4+FG+NH=200+10=210(cm)，
故答案为210
7．(2020·湖南益阳市·七年级期末)如图所示，在长方形ABCD中，AB＝10cm，BC＝6cm，将长方形ABCD沿着AB方向平移________cm，才能使平移后的长方形HEFG与原来的长方形ABCD重叠部分的面积为24cm2．

【答案】6
【详解】解：设AE=x，根据题意列出方程：
6(10-x)=24，
解得x=6，
∵A的对应点为E，∴平移距离为AE的长，
故向右平移6cm．
8．(2020·河北衡水市·七年级期末)如图，直角△ABC中，AC=3，BC=4，AB=5，则内部五个小直角三角形的周长为_____．

【答案】12
【解析】解：由图形可以看出：内部小三角形直角边是大三角形直角边平移得到的，
故内部五个小直角三角形的周长为AC+BC+AB=12．
故答案为12．
考点5：平行线性质与判定的综合问题
典例：(2020·重庆沙坪坝区·七年级期末)如图1，AB∥CD，直线AE分别交AB、CD于点A、E．点F是直线AE上一点，连结BF，BP平分∠ABF，EP平分∠AEC，BP与EP交于点P．

(1)若点F是线段AE上一点，且BF⊥AE，求∠P的度数；
(2)若点F是直线AE上一动点(点F与点A不重合)，请直接写出∠P与∠AFB之间的数量关系．
【答案】(1)45°；(2)当E点在A点上方时，∠BPE＝∠AFB，当E点在A点下方时，∠BPE＝90°﹣∠AFB
【详解】解：(1)过点P作PQ∥AB，过点F作FH∥AB，
∵AB∥CD，
∴AB∥CD∥PQ∥FH，
∴∠ABP＝∠BPQ，∠CEP＝∠EPQ，∠ABF＝∠BFH，∠CEF＝∠EFH，
∴∠ABP+∠CEP＝∠BPQ+∠EPQ＝∠BPE，∠ABF+∠CEF＝∠BFH+∠EFH＝∠BFE，
∵BF⊥AE，
∴∠ABF+∠CEF＝∠BFE＝90°，
∵BP平分∠ABF，EP平分∠AEC，
∴∠ABP+∠CEP＝(∠ABF+∠CEF)＝45°，
∴∠BPE＝45°；

(2)①当点F在EA的延长线上时，∠BPE＝∠AFB，理由如下：
如备用图1，

过点P作PQ∥AB，过点F作FH∥AB，
∵AB∥CD，
∴AB∥CD∥PQ∥FH，
∴∠ABP＝∠BPQ，∠CEP＝∠EPQ，∠ABF＝∠BFH，∠CEF＝∠EFH，
∴∠CEP﹣∠ABP＝∠EPQ﹣∠BPQ＝∠BPE，∠CEF﹣∠ABF＝∠EFH﹣∠BFH＝∠BFE，
∵BP平分∠ABF，EP平分∠AEC，
∴∠CEP﹣∠ABP＝(∠CEF﹣∠ABF)＝∠BFE＝∠AFB，
∴∠BPE＝∠AFB；
②当点F在线段AE上(不与A点重合)时，∠BPE＝90°﹣∠AFB；理由如下：
如备用图2，

过点P作PQ∥AB，过点F作FH∥AB，
∵AB∥CD，
∴AB∥CD∥PQ∥FH，
∴∠ABP＝∠BPQ，∠CEP＝∠EPQ，∠ABF＝∠BFH，∠CEF＝∠EFH，
∴∠ABP+∠CEP＝∠BPQ+∠EPQ＝∠BPE，∠ABF+∠CEF＝∠BFH+∠EFH＝∠BFE，
∵BP平分∠ABF，EP平分∠AEC，
∴∠ABP+∠CEP＝(∠ABF+∠CEF)，
∴∠BPE＝∠BFE
∴∠BFE＝180°﹣∠AFB，
∴∠BPE＝90°﹣∠AFB；
③当点F在AE的延长线上时，∠BPE＝90°﹣∠AFB，理由如下：如备用图3，

过点P作PQ∥AB，过点F作FH∥AB，
∵AB∥CD，
∴AB∥CD∥PQ∥FH，
∴∠ABP＝∠BPQ，∠CEP＝∠EPQ，180°﹣∠ABF＝∠BFH，∠AEC＝∠EFH，
∴∠CEP+∠ABP＝∠EPQ+∠BPQ＝∠BPE，∠BFH﹣∠EFH＝180°﹣∠ABF﹣∠AEC＝∠AFB，
∵BP平分∠ABF，EP平分∠AEC，
∴∠CEP+∠ABP＝(∠AEC+∠ABF)＝(180°﹣∠AFB)，
∴∠BPE＝90°﹣∠AFB；
综上，当E点在A点上方时，∠BPE＝∠AFB，当E点在A点下方时，∠BPE＝90°﹣∠AFB．
方法或规律点拨
此题考查平行线的性质：两直线平行内错角相等，两直线平行同位角相等，两直线平行同旁内角互补，以及角平分线的性质，在相交线问题中通常作平行线利用平行线的性质解答，将角度转化由此求出答案．解题中运用分类思想解答问题．
巩固练习
1．(2020·黑龙江哈尔滨市·七年级期末)已知：直线分别与直线，交于点，．平分，平分，并且．

(1)如图1，求证：；
(2)如图2，，在不添加任何辅助线的情况下，请直接写出图2中四个角，使写出的每个角的度数都为．
【答案】(1)见解析；(2)，，，
【详解】(1)证明：∵，∴．
∵平分，平分，∴，．
∴．
∴．
(2)由(1)知ABCD，
∴∠AEF+∠CFE=180°，
∵∠AEF=2∠CFN=∠CFE，
∴∠AEF=∠CFE=90°，
∴∠CFN=∠EFN=∠FEM=∠BEM=45°，∠BEG=∠CFH=∠DFE=90°,
∴∠AEM=∠GEM=∠HFN=∠DFN=90°+45°=135°，
∴度数为135°的角有：、 、 、 ．
2．(2020·福建福州市·七年级期末)已知两条直线l1，l2，l1∥l2，点A，B在直线l1上，点A在点B的左边，点C，D在直线l2上，且满足．

(1)如图①，求证：AD∥BC；
(2)点M，N在线段CD上，点M在点N的左边且满足，且AN平分∠CAD；
(Ⅰ)如图②，当时，求∠DAM的度数；
(Ⅱ)如图③，当时，求∠ACD的度数．
【答案】(1)证明见解析；(2)(Ⅰ)；(Ⅱ)．
【详解】(1)，
，
又，
，
；
(2)(Ⅰ)，
，
，
，
由(1)已得：，
，
；
(Ⅱ)设，则，
平分，
，
，
，
，
由(1)已得：，
，即，
解得，
，
又，
．
3．(2021·全国七年级)(探究)如图①，，点E在直线，之间．求证：．
(应用)如图②，，点E在直线，之间．若，，，平分，平分，则的大小为_________．

【答案】探究：见解析；应用：
【详解】探究：过点E作
∴，
∵，
∴．
∴，
∵，
∴．
∴．

应用：，
作HP∥AB，
∠BAH=∠AHP，
∵，
∴．
∴∠PHF=∠HFD，
∵平分，平分，
∴∠BAH=∠BAE，∠HFD=∠GFD，
∵GF∥CE，
∴∠ECD=∠GFD，
由(1)知∠BAE+∠ECD=∠AEC=90º，
∴∠BAE+∠GFD=90º，
∴∠AHF=∠AHP+∠PHF=∠BAH+∠HFD=∠BAE+∠GFD=，
∠AHF= ．
故答案为：45º．

4．(2020·山东省青岛第五十九中学八年级期末)已知，，，试解答下列问题：

(1)如图①，则__________，则与的位置关系为__________
(2)如图②，若点E、F在线段上，且始终保持，．则的度数等于__________；
(3)在第(2)题的条件下，若平行移动到图③所示
①在移动的过程中，与的数量关系是否发生改变，若不改变，求出它们之间的数量关系；若改变，请说明理由．
②当时，求的度数．
【答案】(1)72°，平行；(2)36°；(3)①∠OCB=∠OFB；②∠OCA=54°．
【详解】解：(1)∵BC∥OA，
∴∠B+∠O=180°，
∵∠B=108°，
∴∠O=72°，
∵∠A=108°，
∴∠O+∠A=180°，
∴OB∥AC，
故答案为：72°，平行；
(2)∵∠FOC=∠AOC， ，∠BOA=72°，
∴，
故答案为：36°；
(3)①不变，
∵BC∥OA，
∴∠OCB=∠AOC，
又∵∠FOC=∠AOC，
∴∠FOC=∠OCB，
又∵BC∥OA，
∴∠OFB=∠FOA=2∠FOC，
∴∠OFB=2∠OCB，
即∠OCB：∠OFB=1：2．
即∠OCB=∠OFB；
②由(1)知：OB∥AC，
∴∠OCA=∠BOC，
由(2)可以设：∠BOE=∠EOF=α，∠FOC=∠COA=β，
∴∠OCA=∠BOC=2α+β
由(1)知：BC∥OA，
∴∠OEB=∠EOA=α+β+β=α+2β
∵∠OEB=∠OCA
∴2α+β=α+2β
∴α=β
∵∠AOB=72°，
∴α=β=18°
∴∠OCA=2α+β=36°+18°=54°．
5．(2020·浙江杭州市·七年级其他模拟)已知：和同一平面内的点．
(1)如图1，点在边上，过作交于，交于．根据题意，在图1中补全图形，请写出与的数量关系，并说明理由；
(2)如图2，点在的延长线上，，．请判断与的位置关系，并说明理由．
(3)如图3，点是外部的一个动点．过作交直线于，交直线于，直接写出与的数量关系，并在图3中补全图形．

【答案】(1)图见解析，，理由见解析；(2)，理由见解析；(3)图见解析，或．
【详解】
(1)由题意，补全图形如下：

，理由如下：
，
，
，
，
；
(2)，理由如下：
如图，延长BA交DF于点O，
，
，
，
，
；

(3)由题意，有以下两种情况：
①如图3-1，，理由如下：
，
，
，
，
，
由对顶角相等得：，
；

②如图3-2，，理由如下：
，
，
，
，
．

6．(2020·惠州市江南学校八年级期中)已知△ABC中，点D是AC延长线上的一点，过点D作DE∥BC，DG平分∠ADE，BG平分∠ABC，DG与BG交于点G．

(1)如图1，若∠ACB＝90°，∠A＝50°，直接求出∠G的度数；
(2)如图2，若∠ACB≠90°，试判断∠G与∠A的数量关系，并证明你的结论；
【答案】(1) 25º，(2)结论是：∠G=∠A，证明见详解．
【详解】如图，在△ABC中，∠ACB＝90°，∠A＝50°，
∴∠A+∠ABC=90º,
∴∠ABC=90º-∠A=40º，
∵BG平分∠ADE，
∴∠GBC=∠ABG=∠ABC=20º，
由作法DE∥BC，
∠CDE+∠DCF=180º，∠DCF=∠ACB＝90°，
∴∠CDE=90º,
∵DG平分∠ADE，
∴∠CDF=∠EDF=45º,
由DE∥BC，
∴∠BFD=∠EDF=45º,
由外角性质∠BFD=∠G+∠GBF，
∴∠G=∠BFD-∠GBF=45º-20º=25º，

(2)如图， 结论是：∠G=∠A，
∵DE∥BC，
∴∠CFD=∠FDE，
过点C作CH∥DG交BG于H，
∠BHC=∠G，
∵DG平分∠ADE，
∴∠CDF=∠FDE=∠ADE，
∴∠ACH=∠CDG，∠HCF=∠CFD=∠FDE，
∴∠ACH=∠HCF=∠ACF,
∵BG平分∠ABC，
∴∠ABG=∠GBF=∠ABC，
由外角性质∠ACF=∠A+∠ABC，
2∠HCF=∠A+2∠HBC①，
∠HCF=∠HBC+∠BHC②
由②×2-①得，∠BHC=∠A，
∠G=∠A．

7．(2019·河北保定市·八年级月考)如图1所示的是北斗七星的位置图，图2将北斗七星分别标为，，，，，，，并顺次首尾连接，若恰好经过点，且，．
(1)求的度数．
(2)连接，当与满足怎样的数量关系时，，并说明理由．

【答案】(1)75°；(2)当∠ADE+∠CGF=180°时，BC∥AD．
【详解】解：(1)∵AF∥DE，
∴∠F+∠E=180°，
∵
∴∠F=180°-105°=75°；
(2)如图，

当∠ADE+∠CGF=180°时，BC∥AD，
∵AF∥DE，
∴∠GAD+∠ADE=180°，∠ADE+∠CGF=180°，
∴∠GAD=∠CGF，
∴BC∥AD．
8．(2018·上海七年级零模)已知：AB∥DE．

(1)如图1，点C是夹在AB和DE之间的一点，当AC⊥CD时，垂足为点C，你知道∠A+∠D是多少吗？这一题的解决方法有很多，
例如(i)过点C作AB的平行线；
(ii)过点C作DE的平行线；
(iii)联结AD；
(iv)延长AC、DE相交于一点．请你选择一种方法(可以不选上述四种)，并说明理由．
(2)如图2，点C1、C2是夹在AB和DE之间的两点，请想一想：∠A+∠C1+∠C2++∠D= 度，并说明理由．
(3)如图3，随着AB与CD之间点增加，那么∠A+∠C1+∠C2++…+∠Cn+1+∠D= 度．(不必说明理由)
【答案】(1)；(2)540，理由见解析；(3)
【详解】
(1)如图1，过点作的平行线，
∵，∴，
∴，，
∴，
又∵，∴．
(2)如图2，过作，过作，则
∵，∴，
∴，，，
∴，
故答案为：540；
(3)如图3，由(1)(2)可得：
，
故答案为：．

9．(2019·河北唐山市·七年级期中)根据所给图形及已知条件，回答下列问题：

(1)①如图1所示，已知直线，，那么根据_________可得________；
②如图2，在①的条件下，如果平分，则________；
③如图3，在①、②的条件下，如果，则________．
(2)尝试解决下列问题：如图4，已知，，是的平分线，，求的度数．
【答案】(1)①两直线平行，内错角相等；68 ②34 ③56；(2)21°
【详解】解：(1)①两直线平行，内错角相等；∠ABC＝68°，
故填：68；
②∵平分，
∴＝34°，
故填：34 ；
③∵，
∴ ∠NCM＝90°，
∴90°－56°，
故填：56；
(2)∵AB∥CD，
∴∠ABC＋∠BCE＝180°，
∵∠ABC＝42°，
∴∠BCE＝180°－∠ABC＝180°－42°＝138°，
∵CN平分∠BCE，
∴∠BCN＝∠BCE＝69°，
∵CN⊥CM，
∴∠MCN＝90°，
∴∠BCM＝∠MCN－∠BCN＝90°－69°＝21°．
10．(2020·洛阳市第二外国语学校七年级期中)如图1，D是△ABC延长线上的一点，CEAB．
(1)求证：∠ACD＝∠A+∠B；
(2)如图2，过点A作BC的平行线交CE于点H，CF平分∠ECD，FA平分∠HAD，若∠BAD＝70°，求∠F的度数．
(3)如图3，AHBD，G为CD上一点，Q为AC上一点，GR平分∠QGD交AH于R，QN平分∠AQG交AH于N，QMGR，猜想∠MQN与∠ACB的关系，说明理由．

【答案】(1)证明见解析；(2)∠F=55°；(3)∠MQN＝∠ACB；理由见解析．
【详解】解：(1)∵CEAB，
∴∠ACE＝∠A，∠ECD＝∠B，
∵∠ACD＝∠ACE+∠ECD，
∴∠ACD＝∠A+∠B；
(2)∵CF平分∠ECD，FA平分∠HAD，
∴∠FCD＝∠ECD，∠HAF＝∠HAD，
∴∠F＝∠HAD+∠ECD＝(∠HAD+∠ECD)，
∵CHAB，
∴∠ECD＝∠B，
∵AHBC，
∴∠B+∠HAB＝180°，
∵∠BAD＝70°，
，
∴∠F＝(∠B+∠HAD)＝55°；
(3)∠MQN＝∠ACB，理由如下：
平分，
．
平分，
．
，
．
∴∠MQN＝∠MQG﹣∠NQG
＝180°﹣∠QGR﹣∠NQG
＝180°﹣(∠AQG+∠QGD)
＝180°﹣(180°﹣∠CQG+180°﹣∠QGC)
＝(∠CQG+∠QGC)
＝∠ACB．
考点6：与平行线、交线有关的作图问题
典例：(2021·江苏泰州市·七年级期末)如图是由相同边长的小正方形组成的网格图形，小正方形的边长为1个单位长度，每个小正方形的顶点都叫做格点，的三个顶点都在格点上，利用网格画图．(注：所画格点、线条用黑色水笔描黑)

(1)过点画的垂线，并标出垂线所过格点；
(2)过点画的平行线，并标出平行线所过格点；
(3)画出向右平移8个单位长度后的位置；
(4)的面积为______．
【答案】(1)见解析；(2)见解析；(3)见解析；(4)9.5
【详解】解：(1)如图所示，AP是的垂线；为所求格点；
(2)如图所示，，、为所求格点；
(3)如图所示，为所求；

(4)的面积，
故答案为：．
方法或规律点拨
此题主要考查了应用设计与作图，正确掌握相关性质以及结合网格画出对应点是解题关键．
巩固练习
1．(2021·江苏南京市·七年级期末)如图，所有小正方形的边长都为1个单位，A、B、C均在格点上．

(1)过点A画线段BC的垂线，垂足为E；
(2)过点A画线段AB的垂线，交线段CB的延长线于点F；
(3)线段BE的长度是点 到直线 的距离；
(4)线段AE、BF、AF的大小关系是 ．(用“＜”连接)
【答案】(1)见解析；(2)见解析；(3)B，AE；(4)AE＜AF＜BF
【详解】(1)如图所示；
(2)如图所示；

(3) ∵，
∴线段BE的长度是点B到直线AE的距离，
故答案是：B，AE；
(4)∵AE是直角三角形AEF的直角边，AF是直角三角形AEF的斜边，
∴，
∵BF是直角三角形ABF的斜边，AF是直角三角形ABF的直角边，
∴，
∴，
故答案是：．
2．(2021·浙江宁波市·七年级期末)如图，已知同一平面内四个点，，，．

(1)同时过，，两点能作几条直线？作图并写出理由；
(2)在直线上画出符合下列条件的点和，并说明理由．
①使线段长度最小；
②使最小．
【答案】(1)1条，两点确定一条直线，见解析；(2)①见解析；②见解析
【详解】解：(1)根据直线的公理：两点确一条直线，所以同时过，，两点能作1条直线，如图所示：直线AC即为所求，

答：同时过，，两点能作1条直线，因为两点确定一条直线；
(2)如图，① 直线外一点与直线上各点连接的所有线段中，垂线段最短，
过点D作于点P，
则点P即为所求作的点；
②两点之间，线段最短，
画线段BD，交直线AC于点Q，则点Q即为所求作的点

3．(2021·江苏南京市·七年级期末)在如图，所示的方格纸中不用量角器与三角尺，仅用直尺．

(1)经过点画的平行线．
(2)过点，画的垂线．
(3)过点，画的垂线．
(4)请直接写出、的位置关系．
【答案】(1)答案见解析；(2)答案见解析；(3)答案见解析；(4)平行．
【详解】
(1)如图，直线PQ即为所求．
(2)如图，直线AM即为所求．
(3)如图，直线CN即为所求．
(4)∵，，
∴
故AM与CN的位置关系为平行 ．

4．(2020·北京七年级期末)如图，已知直线AB及直线AB外一点P，按下列要求完成画图和解答：(1)连接PA，PB，用量角器画出∠APB的平分线PC，交AB于点C；
(2)过点P作PD⊥AB于点D；
(3)用刻度尺取AB中点E，连接PE；
(4)根据图形回答：点P到直线AB的距离是线段 的长度．

【答案】(1)答案见解析；(2)答案见解析；(3)答案见解析；(4)PD．
【详解】解：(1)、如图所示；(2)、如图所示；(3)、如图所示；

(4)、PD．
5．(2020·莆田擢英中学七年级月考)如图，在正方形网格中有一个△ABC，按要求进行下列作图(只借助网格，需要写出结论)．

(1)过点B画出AC的平行线；
(2)画出三角形ABC向右平移5格，再向上平移2格后的△DEF；
(3)若每一个网格的单位长度为a，求三角形ABC的面积．
【答案】(1)见解析；(2)见解析；(3)三角形ABC的面积＝3a2．
【详解】(1)如图，直线BP为所作；
(2)如图，△DEF为所作；
(3)三角形ABC的面积3a×2a=3a2．

6．(2021·河南新乡市·七年级期末)画图并度量，已知点A是直线l上一点，点M、N是直线l外两点，画图：

(1)画线段，并用刻度尺找出它的中点B；
(2)画直线，交直线l于点C，并用量角器画出的平分线；
(3)画出点M到直线l的垂线段，并度量点M到直线l的距离为__．(精确到)
【答案】(1)见详解；(2)见详解；(3)4.0．
【详解】解：(1)如图，连结AM，测得AM=4.5cm，在线段AM上画以A为端点，长为cm的线段AB，点B即是所求线段AM的中点，
；
(2)如图，①用直尺过点M、N画直线MN，

②测出，再画出以点C为顶点，AC为一边的角 ，则CD即为所求的的平分线CD；

(3)如图，用三角板画点M到直线l的垂线段，测得线段MH=4.0cm，
故答案为：4.0cm．

7．(2020·北京延庆区·七年级期中)已知：四点A，B，C，D的位置如图所示，

(1)连接AD；
(2)画射线AB与线段DC的延长线交于点E；
(3)过点B作BF⊥CD于点F．
【答案】(1)图见解析；(2)图见解析；(3)图见解析．
【详解】解：如图：(1)连接AD，
(2)作射线AB，线段DC，并延长线段DC交于射线AB与E，
(3)过点B作BF⊥CD于点F．

8．(2020·巨野县育才实验学校七年级月考)如图，在方格纸中，直线m与n相交于点C，
(1)请过点A画直线AB，使AB⊥m，垂足为点B；
(2)请过点A画直线AD，使AD∥m；交直线n于点D．

【答案】(1)见解析；(2)见解析
【详解】解：(1)如图，直线AB即为所求；
(2)如图，直线AD即为所求．

9．(2020·黑龙江鸡西市·七年级期末)如图，已知点P、Q分别在∠AOB的边OA、OB上，按下列要求画图：

(1)画直线PQ；
(2)过点P画垂直于射线OB的射线PC，垂足为点C；
(3)过点Q画射线OA的垂线段QD，垂足为点D．
【答案】(1)如图所示，见解析；(2)如图所示，见解析；(3)如图所示，见解析；．
【详解】(1)(2)(3)如图所示．

10．(2015·浙江杭州市·七年级单元测试)读语句作图：
(1)作直线AB；
(2)过点P作直线AB的垂线，垂足M；
(3)连结PA；
(4)画射线PB．
根据所作图填空：
①点A与点P的距离是图中线段　　　　　　的长度．
②点P到直线AB的距离是　　　　　　的长度．
③若Q为直线AB上任一点，则PQ与PM的关系是　　　　　　．其数学原理是　　　　　　．

【答案】见解析．
【详解】解：(1)直线AB如图所示；
(2)直线PM如图所示；
(3)线段PA如图所示；
(4)射线PB如图所示．

①点A与点P的距离是图中线段AP的长度；
②点P到直线AB的距离是PM的长度；
③若Q为直线AB上任一点，则PQ与PM的关系是PQ≥PM，其数学原理是直线外一点到直线的距离中，垂线段最短．
故答案为：AP，PM，PQ≥PM，直线外一点到直线的距离中，垂线段最短．
11．(2019·杭州市十三中教育集团(总校)七年级期中)如图，在所给网格图(每个小格均为边长是1的正方形)中完成下列各题：
(1)△ABC经过平移后得到△A1B1C1，请描述这个平移过程；
(2)过点C画AB的平行线CD；
(3)求出△ABC的面积．

【答案】(1)△ABC向下平移4个单位，向左平移5个单位得到△A1B1C1；(2)见解析；(3)5．
【详解】解：(1)△ABC向下平移4个单位，向左平移5个单位得到△A1B1C1；
(2)如图，直线CD即为所求；

(3)S△ABC＝4×4﹣×3×4﹣×1×2﹣×2×4＝16﹣6﹣1﹣4＝5．
12．(2020·河北秦皇岛市·)在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)画出△ABC向左平移3格，再向上平移2格所得的△A1B1C1；
(2)画出△ABC的中线CD和高AH；
(3)求△A1B1C1的面积.

【答案】(1)(2)图见解析(3)5.5
【详解】(1)△A1B1C1为所求；
(2)中线CD，高AH为所求；
S△ABC=

13．(2020·江苏宿迁市·七年级期中)如图，在每个小正方形边长为的方格纸中，的顶点都在方格纸格点上．将向左平移格，再向上平移格．

(1)请在图中画出平移后的；
(2)画出的边上的中线；
(3)图中与的关系是_______；
(4)在平移过程中，线段所扫过的面积为_______．
【答案】(1)见解析；(2)见解析；(3)平行且相等；(4)16
【详解】解：(1)如图，△A′B′C′即为所画图形；
(2)如图，BD即为所画图形；
(3)由平移的性质可得：AC和A′C′平行且相等，
故答案为：平行且相等；
(4)如图，由题意可知平移过程中，
线段AB扫过的区域为四边形A′B′FE，
∴线段AB所扫过的面积为4×4=16，
故答案为：16．

14．(2020·黑龙江哈尔滨市·九年级月考)如图,在边长为1的小正方形组成的12×12的网格中，给出了以格点(网格线的交点)为端点的线段AB．

(1)将线段AB向右平移5个单位，再向上平移3个单位得到线段CD，点A、B的对应点分别为C、D，请画出线段CD；
(2)以线段CD为一边，作一个菱形CDEF，点E、F都为格点，且菱形CDEF的面积为5．(作出一个菱形即可)，直接写出对角线DF的长．
【答案】(1)作图见解析；(2)作图见解析，．
【详解】
(1)作图如图所示；

(2)作图如图所示

由图可知，，
∵菱形CDEF的面积为5，
∴,
∴．