

2021-2022学年广东省广州市部分学校八年级(上)期中数学试卷 解析版
展开2021-2022学年广东省广州市部分学校八年级(上)期中数学试卷
一、选择题(共10小题,共30分)
1.(3分)在以下大众、东风、长城、奔驰四个汽车标志中,不是轴对称图形的是( )
A. B.
C. D.
2.(3分)下列长度的3条线段,能首尾依次相接组成三角形的是( )
A.1cm,2cm,4cm B.8cm,6cm,4cm
C.12cm,5cm,6cm D.1cm,3cm,4cm
3.(3分)如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是( )
A.∠C=∠B B.DF∥AE C.∠A+∠D=90° D.CF=BE
4.(3分)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.45° B.60° C.75° D.90°
5.(3分)如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
A.65° B.50° C.60° D.57.5°
6.(3分)点P(2,﹣5)关于x轴对称的点的坐标为( )
A.(﹣2,5) B.(2,5) C.(﹣2,﹣5) D.(2,﹣5)
7.(3分)如图,若AB=AC,则添加下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.∠B=∠C B.AE=AD C.BE=CD D.∠AEB=ADC
8.(3分)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
9.(3分)在平面直角坐标系中,已知A(2,2),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有( )
A.2个 B.3个 C.4个 D.5个
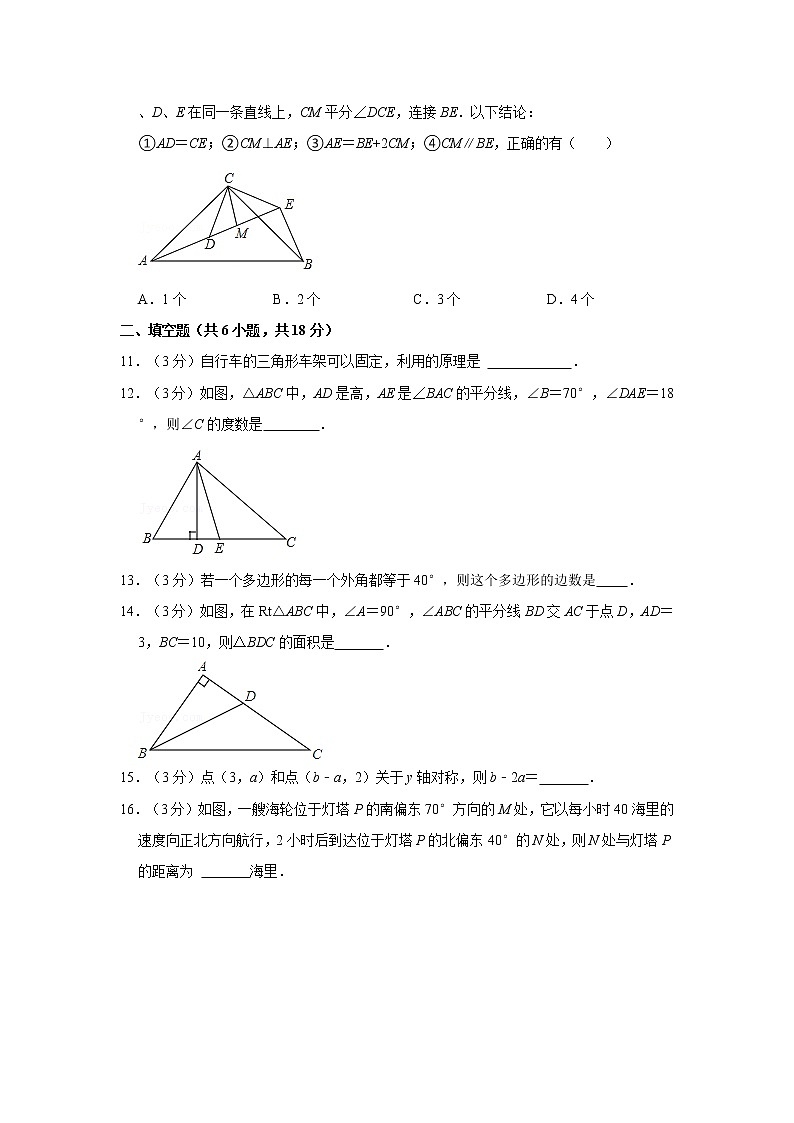
10.(3分)如图,△ACB和△DCE均为等腰直角三角形,且∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM平分∠DCE,连接BE.以下结论:
①AD=CE;②CM⊥AE;③AE=BE+2CM;④CM∥BE,正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6小题,共18分)
11.(3分)自行车的三角形车架可以固定,利用的原理是 .
12.(3分)如图,△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠DAE=18°,则∠C的度数是 .
13.(3分)若一个多边形的每一个外角都等于40°,则这个多边形的边数是 .
14.(3分)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
15.(3分)点(3,a)和点(b﹣a,2)关于y轴对称,则b﹣2a= .
16.(3分)如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 海里.
三、解答题(共9小题,共72分)
17.(6分)已知:如图,AB=CD,AD=BC.求证:AB∥CD.
18.(6分)如图,在△ABC中,AB=AC,点D在BA的延长线上.
(1)尺规作图:作∠DAC的角平分线AE(不写作法,保留作图痕迹);
(2)若∠C=28°,则∠CAE的度数为 .
19.(6分)已知等腰三角形的周长为18cm,其中两边之差为3cm,求三角形的各边长.
20.(6分)如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.
21.(8分)如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?
(要求:尺规作图,不写作法,但要保留作图痕迹,并写出结论)
22.(8分)在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;并直接写出A1,B1,C1的坐标.
(3)请在y轴上求作一点P,使△PB1C的周长最小.
23.(8分)如图,在平面直角坐标系中,点A的坐标为(2,0),点B从原点O出发,以每秒1个单位的速度沿y轴正方向匀速运动,设点B的运动时间为t秒,过点B作CB⊥AB,且CB=AB.
(1)若∠CBO=60°,则BC= ;
(2)求点C的坐标(用含t的代数式表示).
24.(12分)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线D交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)证明:BM=CN;
(2)当∠BAC=70°时,求∠DCB的度数.
25.(12分)△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子的值会发生变化吗?若不变,求出该值;若变化请说明理由.
2021-2022学年广东省广州市部分学校八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(共10小题,共30分)
1.(3分)在以下大众、东风、长城、奔驰四个汽车标志中,不是轴对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形的概念分别分析求解.
【解答】解:A、轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项正确;
C、是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项错误.
故选:B.
2.(3分)下列长度的3条线段,能首尾依次相接组成三角形的是( )
A.1cm,2cm,4cm B.8cm,6cm,4cm
C.12cm,5cm,6cm D.1cm,3cm,4cm
【分析】根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,分别判断出即可.
【解答】解:∵三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,
∵1+2<4,∴无法围成三角形,故此选项A错误;
∵4+6>8,∴能围成三角形,故此选项B正确;
∵5+6<12,∴无法围成三角形,故此选项C错误;
∵1+3=4,∴无法围成三角形,故此选项D错误.
故选:B.
3.(3分)如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是( )
A.∠C=∠B B.DF∥AE C.∠A+∠D=90° D.CF=BE
【分析】根据HL证明Rt△CFD≌Rt△BEA,利用全等三角形的性质即可一一判断.
【解答】解:∵CE=BF,
∴CE﹣EF=BF=EF,
∴CF=BE,
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△CFD和Rt△BEA中,
,
∴Rt△CFD≌Rt△BEA(HL),
∴∠C=∠B,∠D=∠A,
∴CD∥AB,故A,B,D正确,
∵∠C+∠D=90°,
∴∠A+∠C=90°,故C错误,
故选:C.
4.(3分)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.45° B.60° C.75° D.90°
【分析】根据直角三角形的两锐角互余求出∠1的度数,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【解答】解:如图,∠1=90°﹣60°=30°,
所以,∠α=45°+30°=75°.
故选:C.
5.(3分)如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )
A.65° B.50° C.60° D.57.5°
【分析】先根据图形翻折不变性的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算即可求解.
【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=65°,
∴∠BDF=180°﹣∠B﹣∠BFD=180°﹣65°﹣65°=50°.
故选:B.
6.(3分)点P(2,﹣5)关于x轴对称的点的坐标为( )
A.(﹣2,5) B.(2,5) C.(﹣2,﹣5) D.(2,﹣5)
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
【解答】解:∵点P(2,﹣5)关于x轴对称,
∴对称点的坐标为:(2,5).
故选:B.
7.(3分)如图,若AB=AC,则添加下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.∠B=∠C B.AE=AD C.BE=CD D.∠AEB=ADC
【分析】根据ASA即可判断A;根据SAS即可判断B;根据SSA两三角形不一定全等即可判断C;根据AAS即可判断D.
【解答】解:A、根据ASA(∠A=∠A,∠C=∠B,AB=AC)能推出△ABE≌△ACD,正确,故本选项错误;
B、根据SAS(∠A=∠A,AB=AC,AE=AD)能推出△ABE≌△ACD,正确,故本选项错误;
C、两边和一角对应相等的两三角形不一定全等,错误,故本选项正确;
D、根据AAS(∠A=∠A,AB=AC,∠AEB=∠ADC)能推出△ABE≌△ACD,正确,故本选项错误;
故选:C.
8.(3分)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
【分析】由于凉亭到草坪三条边的距离相等,所以根据角平分线上的点到边的距离相等,可知是△ABC三条角平分线的交点.由此即可确定凉亭位置.
【解答】解:∵凉亭到草坪三条边的距离相等,
∴凉亭选择△ABC三条角平分线的交点.
故选:C.
9.(3分)在平面直角坐标系中,已知A(2,2),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有( )
A.2个 B.3个 C.4个 D.5个
【分析】此题应该分情况讨论.以OA为腰或底分别讨论,进而得出答案.
【解答】解:(1)若AO作为腰时,有两种情况,
①当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有1个,若OA是底边时,P是OA的中垂线与x轴的交点,有1个,
②当O是顶角顶点时,P是以O为圆心,以OA为半径的圆与x轴的交点,有2个;
(2)若OA是底边时,P是OA的中垂线与x轴的交点,有1个,
以上4个交点没有重合的.故符合条件的点有4个.
故选:C.
10.(3分)如图,△ACB和△DCE均为等腰直角三角形,且∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM平分∠DCE,连接BE.以下结论:
①AD=CE;②CM⊥AE;③AE=BE+2CM;④CM∥BE,正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】由“SAS”可证△ACD≌△BCE,可得AD=BE,∠ADC=∠BEC,可判断①,由等腰直角三角形的性质可得∠CDE=∠CED=45°.CM⊥AE,可判断②,由全等三角形的性质可求∠AEB=∠CME=90°,可判断④,由线段和差关系可判断③,即可求解.
【解答】解:∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,故①错误,
∵△DCE为等腰直角三角形,CM平分∠DCE,
∴∠CDE=∠CED=45°,CM⊥AE,故②正确,
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°,
∴∠AEB=∠CME=90°,
∴CM∥BE,故④正确,
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.故③正确,
故选:C.
二、填空题(共6小题,共18分)
11.(3分)自行车的三角形车架可以固定,利用的原理是 三角形的稳定性 .
【分析】利用三角形的稳定性进行解答.
【解答】解:自行车的三角形车架可以固定,利用的原理是三角形的稳定性.
故答案为:三角形的稳定性.
12.(3分)如图,△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠DAE=18°,则∠C的度数是 34° .
【分析】根据三角形内角和定理求出∠BAD,根据角平分线的定义求出∠BAC,根据三角形内角和定理计算即可.
【解答】解:∵△ABC中,AD是高,∠B=70°,
∴∠BAD=20°,
∴∠BAE=38°,
∵AE是∠BAC的平分线,
∴∠BAC=76°,
∴∠C=180°﹣76°﹣70°=34°,
故答案为:34°.
13.(3分)若一个多边形的每一个外角都等于40°,则这个多边形的边数是 9 .
【分析】根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.
【解答】解:360÷40=9,即这个多边形的边数是9.
14.(3分)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 15 .
【分析】过D作DE⊥BC于E,根据角平分线性质求出DE=3,根据三角形的面积求出即可.
【解答】解:过D作DE⊥BC于E,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴AD=DE=3,
∴△BDC的面积是×DE×BC=×10×3=15,
故答案为:15.
15.(3分)点(3,a)和点(b﹣a,2)关于y轴对称,则b﹣2a= ﹣5 .
【分析】根据关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变,即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),可得a、b的值,再代入所求式子计算即可.
【解答】解:∵点(3,a)和点(b﹣a,2)关于y轴对称,
∴a=2,b﹣a=﹣3,
解得a=2,b=﹣1,
∴b﹣2a=﹣1﹣4=﹣5.
故答案为:﹣5.
16.(3分)如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 80 海里.
【分析】根据平角的性质得到∠NPM=180°﹣70°﹣40°=70°,根据平行线的性质得到∠M=70°,求得∠NPM=∠M,根据等腰三角形的性质健康得到结论.
【解答】解:∵∠NPM=180°﹣70°﹣40°=70°,
∵向北的方向线是平行的,
∴∠M=70°,
∴∠NPM=∠M,
∴NP=MN=40×2=80(海里),
故答案为:80.
三、解答题(共9小题,共72分)
17.(6分)已知:如图,AB=CD,AD=BC.求证:AB∥CD.
【分析】根据全等三角形对应角相等得出∠ABD=∠CDA,进一步得出AB∥CD.
【解答】证明:在△ABD与△CDB中,
,
∴△ABD≌△CDB,
∴∠ABD=∠CDA,
∴AB∥CD.
18.(6分)如图,在△ABC中,AB=AC,点D在BA的延长线上.
(1)尺规作图:作∠DAC的角平分线AE(不写作法,保留作图痕迹);
(2)若∠C=28°,则∠CAE的度数为 28° .
【分析】(1)利用基本作图,作∠DAC的平分线即可;
(2)利用AB=AC得到∠C=∠B=28°,再根据三角形外角性质得到∠DAE=56°,然后根据角平分线的定义求解.
【解答】解;(1)如图,AE为所作;
(2)∵AB=AC,
∴∠C=∠B=28°,
∴∠DAE=∠B+∠C=56°,
∵AE平分∠DAC,
∴CAE=∠DAC=28°.
故答案为28°.
19.(6分)已知等腰三角形的周长为18cm,其中两边之差为3cm,求三角形的各边长.
【分析】已知等腰三角形的周长为18cm,两边之差为6cm,但没有明确指明底边与腰谁大,因此要分两种情况,分类讨论.
【解答】解:设三角形的腰为x,底为y,
根据题意得或
解得或,
所以等腰三角形的腰与底边的长分别为:7cm,4cm或5cm,8cm;
20.(6分)如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.
【分析】根据∠DCB=2∠B,以及角平分线的性质得出∠ACD与∠B的关系,再根据三角形内角和定理即可求解.
【解答】解:∵CD是∠ACB的平分线,
∴∠ACD=∠DCB,
∵∠DCB=2∠B,
∴∠ACD=∠DCB=2∠B,
又∵∠A=90°,
∴∠ACD+∠DCB+∠B=90°,
∴2∠B+2∠B+∠B=90°,
∴∠B=18°,
∴∠ACD=36°.
21.(8分)如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P应建在什么位置?
(要求:尺规作图,不写作法,但要保留作图痕迹,并写出结论)
【分析】由条件可知发射塔要再两条高速公路的夹角的角平分线和线段AB的中垂线的交点上,分别作出夹角的角平分线和线段AB的中垂线,找到其交点就是发射塔修建位置.
【解答】解:分别作出公路夹角的角平分线和线段AB的中垂线,他们的交点为P,则P点就是修建发射塔的位置.
22.(8分)在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;并直接写出A1,B1,C1的坐标.
(3)请在y轴上求作一点P,使△PB1C的周长最小.
【分析】(1)利用点A和C点坐标画出直角坐标系;
(2)利用关于x轴对称的点的坐标特征写出点A1,B1,C1的坐标,然后描点即可;
(3)作C点关于y轴的对称点C′,连接C′B1交y轴于P点,利用两点之间线段最短可判断P点满足条件.
【解答】解:(1)如图,
(2)如图,△A1B1C1为所作;A1(﹣4,﹣6),B1(﹣2,﹣2),C1(﹣1,﹣4);
(3)如图,点P为所作.
23.(8分)如图,在平面直角坐标系中,点A的坐标为(2,0),点B从原点O出发,以每秒1个单位的速度沿y轴正方向匀速运动,设点B的运动时间为t秒,过点B作CB⊥AB,且CB=AB.
(1)若∠CBO=60°,则BC= 4 ;
(2)求点C的坐标(用含t的代数式表示).
【分析】(1)由∠CBO=60°,CB⊥AB得∠ABO=30°,在Rt△AOB中,OA=2,即得AB=4,即可得出结果;
(2)过C作CD⊥OB于D,由CB⊥AB,得∠ABO=∠BCD,可证明△CDB≌△BOA(AAS),得出BD=OA=2,CD=OB,即可得出结果.
【解答】解:(1)∵∠CBO=60°,CB⊥AB,
∴∠ABO=30°,
∵∠AOB=90°,OA=2,
∴AB=2OA=4,
∵BC=AB,
∴BC=4,
故答案:4;
(2)过C作CD⊥OB于D,如图所示:
则∠CDB=90°,
∵∠BOA=90°,
∴∠CDB=∠BOA,
∵CB⊥AB,
∴∠ABO=90°﹣∠CBD=∠BCD,
在△CDB和△BOA中,
,
∴△CDB≌△BOA(AAS),
∴BD=OA=2,CD=OB,
由已知可得OB=t,
∴CD=t,OD=OB﹣BD=t﹣2,
∴C的坐标为:(﹣t,t﹣2).
24.(12分)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线D交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)证明:BM=CN;
(2)当∠BAC=70°时,求∠DCB的度数.
【分析】(1)根据角平分线的性质和线段垂直平分线的性质可得到DM=DN,DB=DC,根据HL证明Rt△DMB≌Rt△DNC,即可得出BM=CN;
(2)根据角平分线的性质得到DM=DN,根据全等三角形的性质得到∠ADM=∠ADN,线段垂直平分线的性质和等腰三角形的性质得到∠EDC=55°于是得到结论.
【解答】(1)证明:连接BD,如图所示:
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
∵DE垂直平分线BC,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
,
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN;
(2)解:由(1)得:∠BDM=∠CDN,
∵AD是∠CAB的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△DMA和Rt△DNA中,
,
∴Rt△DMA≌Rt△DNA(HL),
∴∠ADM=∠ADN,
∵∠BAC=70°,
∴∠MDN=110°,∠ADM=∠ADN=55°,
∵∠BDM=∠CDN,
∴∠BDC=∠MDN=110°,
∵DE是BC的垂直平分线,
∴DB=DC,
∴∠EDC=BDC=55°,
∴∠DCB=90°﹣∠EDC=35°,
∴∠DCB=35°.
25.(12分)△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子的值会发生变化吗?若不变,求出该值;若变化请说明理由.
【分析】(1)根据等腰直角三角形的性质得到CD=CE,再利用等角的余角相等得到∠DCB=∠CEF,然后根据“AAS”可证明△DBC≌△CFE;
(2)由△DBC≌△CFE得到BD=CF,BC=EF,再利用△ABC为等腰直角三角形得到AB=BC,所以AB=EF,AD=BF,接着证明△ABM≌△EFM,得到BM=FM,所以=2;
(3)在EH上截取EQ=DG,如图2,先证明△CDG≌△CEQ得到CG=CQ,∠DCG=∠ECQ,由于∠DCG+∠DCB=45°,则∠ECQ+∠DCB=45°,所以∠HCQ=45°,再证明△HCG≌△HCQ,则得到HG=HQ,然后可计算出=1.
【解答】(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
,
∴△DBC≌△CFE;
(2)解:如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
,
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴的值为2;
(3)解:的值不变.
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中
,
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
,
∴△HCG≌△HCQ,
∴HG=HQ,
∴===1.
2022-2023学年广东省广州市天河区八年级(上)期中数学试卷(解析版): 这是一份2022-2023学年广东省广州市天河区八年级(上)期中数学试卷(解析版),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省广州市越秀区育才实验学校2020-2021学年八年级(上)期中数学试卷(解析版): 这是一份广东省广州市越秀区育才实验学校2020-2021学年八年级(上)期中数学试卷(解析版),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年广东省广州市海珠区绿翠学校八年级(上)期中数学试卷 解析版: 这是一份2021-2022学年广东省广州市海珠区绿翠学校八年级(上)期中数学试卷 解析版,共25页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。












