

2021-2022学年河南省安阳市汤阴县九年级(上)期中数学试卷 解析版
展开2021-2022学年河南省安阳市汤阴县九年级(上)期中数学试卷
一、选择题(本题共10小题,每题3分,共计30分)
1.(3分)如图所示的图形中,是中心对称图形的是( )
A. B. C. D.
2.(3分)下列关于x的方程中,一定是一元二次方程的为( )
A.3x2+1=(3x+1)(x﹣5) B.(a2+1)x2+2x﹣3=0
C.2x2+y=5 D.
3.(3分)将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x﹣1)2+4 C.y=(x+1)2+2 D.y=(x﹣1)2+2
4.(3分)组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.x(x+1)=28 B.x(x﹣1)=28
C.x(x﹣1)=28 D.x(x+1)=28
5.(3分)某种商品零售价经过两次降价后,每件的价格由原来的800元降为现在的578元,则平均每次降价的百分率为( )
A.10% B.12% C.15% D.17%
6.(3分)若点(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,那么这条抛物线的对称轴是( )
A.直线x=1 B.直线x=2 C.直线x=3 D.直线x=4
7.(3分)关于二次函数y=x2﹣4x+7,下列说法中正确的是( )
A.函数图象是抛物线,且开口向下
B.函数图象与x轴有两个交点
C.当x≤2时,y随x的增大而增大
D.函数图象的顶点坐标是(2,3)
8.(3分)函数y=x2﹣6x+c的图象过A(﹣1,y1),B(3,y2),C(5,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y3>y1>y2
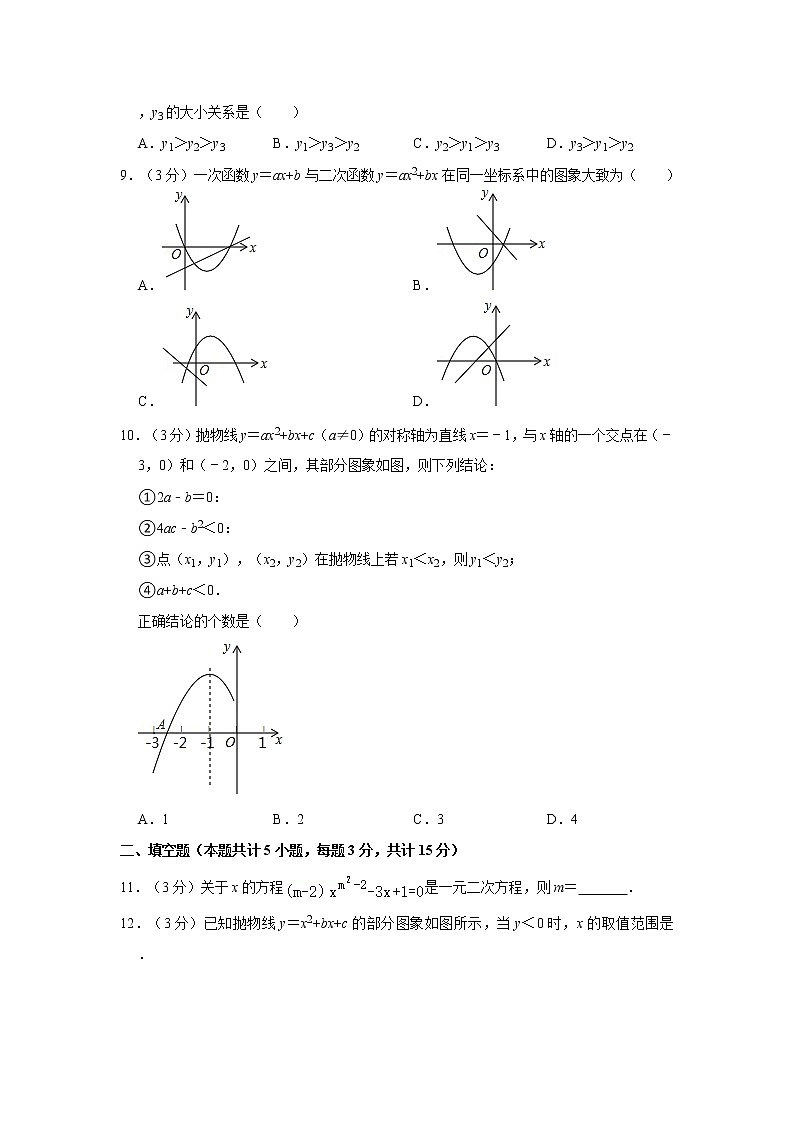
9.(3分)一次函数y=ax+b与二次函数y=ax2+bx在同一坐标系中的图象大致为( )
A. B.
C. D.
10.(3分)抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:
①2a﹣b=0:
②4ac﹣b2<0:
③点(x1,y1),(x2,y2)在抛物线上若x1<x2,则y1<y2;
④a+b+c<0.
正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本题共计5小题,每题3分,共计15分)
11.(3分)关于x的方程是一元二次方程,则m= .
12.(3分)已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是 .
13.(3分)若点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,则xy的值为 .
14.(3分)在平面直角坐标系中,将抛物线y=x2﹣4先向右平移2个单位,再向上平移3个单位,得到的抛物线解析式为 .
15.(3分)设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2﹣1)=12,则a2+b2的值为 .
三、解答题(本题共计8小题,共计75分)
16.(8分)解方程:
(1)3x(x﹣1)=x﹣1.
(2)(y﹣1)2=(3﹣2y)2.
17.(9分)已知二次函数y=﹣x2+2x+k+2与x轴有两个交点.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的交点坐标及顶点坐标.
18.(9分)已知:关于x的一元二次方程x2﹣(m﹣1)x﹣m=0.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根是1,求另一个根.
19.(9分)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于原点对称的图形△A1B1C1,并写出点A1、B1、C1的坐标;
(2)请画出△ABC绕原点O按逆时针方向旋转90°后的图形△A2B2C2,并求出点A2、B2、C2的坐标.
(3)求线段CC2的长.
20.(9分)如图,有一个长为24米的篱笆,一面有围墙(墙的最大长度为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.
(1)求S与x的函数关系式及x的取值范围.
(2)如果要围成的花圃ABCD的面积是45平方米,则AB的长为多少米?
21.(9分)阅读下面的例题:
解方程:x2﹣|x|﹣2=0
解:(1)当x≥0时,原方程化为x2﹣x﹣2=0,解得:x1=2,x2=﹣1(不合题意,舍去).
(2)当x<0时,原方程化为x2+x﹣2=0,解得:x1=1(不合题意,舍去),x2=﹣2
∴原方程的根是x1=2,x2=﹣2.
请参照例题解方程x2﹣|x﹣3|﹣3=0,则此方程的根是 .
22.(10分)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加,某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.并指出该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
23.(12分)如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
2021-2022学年河南省安阳市汤阴县九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共10小题,每题3分,共计30分)
1.(3分)如图所示的图形中,是中心对称图形的是( )
A. B. C. D.
【分析】根据中心对称图形的概念求解.
【解答】解:A、不是中心对称图形,不符合题意;
B、不是中心对称图形,不符合题意;
C、不是中心对称图形,不符合题意;
D、是中心对称图形,符合题意.
故选:D.
2.(3分)下列关于x的方程中,一定是一元二次方程的为( )
A.3x2+1=(3x+1)(x﹣5) B.(a2+1)x2+2x﹣3=0
C.2x2+y=5 D.
【分析】根据一元二次方程的定义逐个判断即可.
【解答】解:A.化简为1=﹣14x﹣5,是一元一次方程,不是一元二次方程,故本选项不符合题意;
B.是一元二次方程,故本选项符合题意;
C.是二元二次方程,不是一元二次方程,故本选项不符合题意;
D.是分式方程,不是整式方程,不是一元二次方程,故本选项不符合题意;
故选:B.
3.(3分)将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x﹣1)2+4 C.y=(x+1)2+2 D.y=(x﹣1)2+2
【分析】本题是将一般式化为顶点式,由于二次项系数是1,只需加上一次项系数的一半的平方来凑成完全平方式即可.
【解答】解:y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2.
故选:D.
4.(3分)组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.x(x+1)=28 B.x(x﹣1)=28
C.x(x﹣1)=28 D.x(x+1)=28
【分析】关系式为:球队总数×每支球队需赛的场数÷2=4×7,把相关数值代入即可.
【解答】解:每支球队都需要与其他球队赛(x﹣1)场,但2队之间只有1场比赛,
所以可列方程为:x(x﹣1)=4×7.
故选:B.
5.(3分)某种商品零售价经过两次降价后,每件的价格由原来的800元降为现在的578元,则平均每次降价的百分率为( )
A.10% B.12% C.15% D.17%
【分析】设平均每次降价的百分率为x,那么第一次降价后为800(1﹣x),第二次降价后为800(1﹣x)(1﹣x),然后根据每件的价格由原来的800元降为现在的578元即可列出方程,解方程即可.
【解答】解:设平均每次降价的百分率为x,
依题意得800(1﹣x)2=578,
∴(1﹣x)2=,
∴1﹣x=±0.85,
∴x=0.15=15%或x=1.85(舍去).
答:平均每次降价的百分率为15%.
故选:C.
6.(3分)若点(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,那么这条抛物线的对称轴是( )
A.直线x=1 B.直线x=2 C.直线x=3 D.直线x=4
【分析】根据抛物线的对称性即可确定抛物线对称轴.
【解答】解:∵点(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,且纵坐标相等.
∴根据抛物线的对称性知道抛物线对称轴是直线x==3.
故选:C.
7.(3分)关于二次函数y=x2﹣4x+7,下列说法中正确的是( )
A.函数图象是抛物线,且开口向下
B.函数图象与x轴有两个交点
C.当x≤2时,y随x的增大而增大
D.函数图象的顶点坐标是(2,3)
【分析】利用二次函数的性质直接对A进行判断;方程x2﹣4x+7=0的判别式小于0可对B进行判断;通过配方把一般式化为顶点式,然后根据二次函数的性质对C、D进行判断.
【解答】解:∵a=1>0,
∴抛物线开口向上,所以A选项的说法错误;
∵y=0时,x2﹣4x+7=0,
而△=42﹣4×7=﹣12<0,
∴函数图象与x轴没有交点,所以B选项的说法错误;
∵y=x2﹣4x+7=(x﹣2)2+3,
∴抛物线的对称轴为直线=2,当x≤2时,y随x的增大而减小,所以C选项的说法错误;
抛物线的顶点坐标为(2,3),所以D选项的说法正确.
故选:D.
8.(3分)函数y=x2﹣6x+c的图象过A(﹣1,y1),B(3,y2),C(5,y3),则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y3>y1>y2
【分析】二次函数抛物线向下,且对称轴为x=﹣=3.根据二次函数的对称性和增减性即可得到结论.
【解答】解:∵二次函数y=x2﹣6x+c,
∴该二次函数的抛物线开口向上,且对称轴为:x=﹣=3.
∵点(﹣1,y1)、(3,y2)、(5,y3)都在二次函数y=x2﹣6x+c的图象上,
∴点(﹣1,y1)关于直线x=3的对称点为(7,y1),
∵3<5<7
∴y2<y3<y1
故选:B.
9.(3分)一次函数y=ax+b与二次函数y=ax2+bx在同一坐标系中的图象大致为( )
A. B.
C. D.
【分析】对于每个选项,先根据二次函数的图象确定a和b的符号,然后根据一次函数的性质看一次函数图象的位置是否正确,若正确,说明它们可在同一坐标系内存在.
【解答】解:A、由二次函数y=ax2+bx的图象得a>0,b<0,则一次函数y=ax+b经过第一、三、四象限,且它们的交点为(1,0),所以A选项正确;
B、由二次函数y=ax2+bx的图象得a>0,b>0,则一次函数y=ax+b经过第一、二、三象限,所以B选项错误;
C、由二次函数y=ax2+bx的图象得a<0,b>0,则一次函数y=ax+b经过第一、二、四象限,所以C选项错误;
D、由二次函数y=ax2+bx的图象得a<0,b<0,则一次函数y=ax+b经过第二、三、四象限,所以D选项错误.
故选:A.
10.(3分)抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:
①2a﹣b=0:
②4ac﹣b2<0:
③点(x1,y1),(x2,y2)在抛物线上若x1<x2,则y1<y2;
④a+b+c<0.
正确结论的个数是( )
A.1 B.2 C.3 D.4
【分析】根据函数与x轴的交点的个数,以及对称轴的解析式,函数值的符号的确定即可作出判断.
【解答】解:①函数的对称轴是直线x=﹣1,即﹣=﹣1,则b=2a,2a﹣b=0,故本选项正确;
②函数与x轴有两个交点,则b2﹣4ac>0,即4ac﹣b2<0,故本选项正确;
③因为不知道点(x1,y1),(x2,y2)在抛物线上所处的位置,所以y1和y2的大小无法判断,则本选项错误.
④∵(﹣3,0)关于直线x=﹣1的对称点是(1,0),且当x=﹣3时,y<0,
∴当x=1时,函数对应的点在x轴下方,则a+b+c<0,则本选项正确;
故选:C.
二、填空题(本题共计5小题,每题3分,共计15分)
11.(3分)关于x的方程是一元二次方程,则m= ﹣2 .
【分析】根据一元二次方程的定义得出m﹣2≠0且m2﹣2=2,再求出m即可.
【解答】解:∵关于x的方程是一元二次方程,
∴m﹣2≠0且m2﹣2=2,
解得:m=﹣2,
故答案为:﹣2.
12.(3分)已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是 ﹣1<x<3 .
【分析】根据函数图象和二次函数的性质,可以得到该抛物线与x轴的另一个交点,从而可以得到当y<0时,x的取值范围.
【解答】解:由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
13.(3分)若点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,则xy的值为 1 .
【分析】直接利用关于原点对称点的性质(两个点关于原点对称时,它们的坐标符号相反)得出x,y的值,进而得出答案.
【解答】解:∵点A(2x﹣1,﹣5)和点B(3,y﹣3)关于原点对称,
∴2x﹣1+3=0,y﹣3﹣5=0,
解得:x=﹣1,y=8,
则xy=(﹣1)8=1.
故答案为:1.
14.(3分)在平面直角坐标系中,将抛物线y=x2﹣4先向右平移2个单位,再向上平移3个单位,得到的抛物线解析式为 y=(x﹣2)2﹣1 .
【分析】先确定抛物线y=x2﹣4的顶点坐标为(0,﹣4),再根据点平移的规律点(0,﹣4)平移后得到点的坐标为(2,﹣1),然后根据顶点式写出平移后抛物线的解析式.
【解答】解:抛物线y=x2﹣4的顶点坐标为(0,﹣4),把点(0,﹣4)先向右平移2个单位,再向上平移3个单位得到点的坐标为(2,﹣1),所以平移后的抛物线解析式为y=(x﹣2)2﹣1.
故答案为y=(x﹣2)2﹣1.
15.(3分)设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2﹣1)=12,则a2+b2的值为 4 .
【分析】把(a2+b2﹣4)(a2+b2+3)=0看作为关于a2+b2的一元二次方程,利用因式分解法可求得a2+b2=4或a2+b2=﹣3,然后根据非负数的性质可确定a2+b2=4.
【解答】解:∵(a2+b2)(a2+b2﹣1)=12,
∴(a2+b2)2﹣(a2+b2)﹣12=0,
∴(a2+b2﹣4)(a2+b2+3)=0,
∴a2+b2﹣4=0或a2+b2+3=0,
∴a2+b2=4或a2+b2=﹣3(舍去).
故答案为4.
三、解答题(本题共计8小题,共计75分)
16.(8分)解方程:
(1)3x(x﹣1)=x﹣1.
(2)(y﹣1)2=(3﹣2y)2.
【分析】(1)利用因式分解法求解即可;
(2)利用因式分解法求解即可.
【解答】解:(1)3x(x﹣1)=x﹣1,
3x(x﹣1)﹣(x﹣1)=0,
(x﹣1)(3x﹣1)=0,
∴x﹣1=0或3x﹣1=0,
∴x1=1,x2=;
(2)(y﹣1)2=(3﹣2y)2,
(y﹣1)2﹣(3﹣2y)2=0,
[(y﹣1)+(3﹣2y)][((y﹣1)﹣(3﹣2y)]=0,
∴﹣y+2=0或3y﹣4=0,
∴y1=2,y2=.
17.(9分)已知二次函数y=﹣x2+2x+k+2与x轴有两个交点.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的交点坐标及顶点坐标.
【分析】(1)由抛物线与x轴有两个交点可得b2﹣4ac>0,进而求解.
(2)将k=1代入函数解析式,然后将解析式配方求顶点坐标,将y=0代入解析式求抛物线与x轴交点坐标.
【解答】解:(1)由题意知b2﹣4ac>0,
∴b2﹣4ac=22﹣4×(﹣1)(k+2)=4k+12>0,
∴k>﹣3.
(2)把k=1代入二次函数得y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线顶点坐标为(1,4).
当y=0时,﹣x2+2x+3=0,
解得x1=3,x2=﹣1
∴抛物线与x轴交点坐标为(﹣1,0),(3,0).
18.(9分)已知:关于x的一元二次方程x2﹣(m﹣1)x﹣m=0.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根是1,求另一个根.
【分析】(1)根据方程的系数结合根的判别式Δ=b2﹣4ac,即可得出Δ=(m+1)2≥0,进而可证出方程总有两个实数根;
(2)将x=1代入原方程可求出m的值,进而可得出原方程,再利用两根之和等于﹣即可求出方程的另一个根.
【解答】(1)证明:∵a=1,b=﹣(m﹣1),c=﹣m,
∴Δ=b2﹣4ac=[﹣(m﹣1)]2﹣4×1×(﹣m)=m2+2m+1=(m+1)2≥0,
∴方程总有两个实数根;
(2)解:将x=1代入原方程,得:12﹣(m﹣1)×1﹣m=0,
解得:m=1,
∴原方程为x2﹣1=0,
∴方程的另一个根为0﹣1=﹣1.
19.(9分)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于原点对称的图形△A1B1C1,并写出点A1、B1、C1的坐标;
(2)请画出△ABC绕原点O按逆时针方向旋转90°后的图形△A2B2C2,并求出点A2、B2、C2的坐标.
(3)求线段CC2的长.
【分析】(1)根据关于原点对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出A、B、C的对应点A2、B2、C2即可,然后写出A2、B2、C2的坐标;
(3)利用勾股定理计算.
【解答】解:(1)如图,△A1B1C1为所作;A1(﹣2,﹣4)、B1(﹣1,﹣1)、C1(﹣4,﹣3);
(2)如图,△A2B2C2为所作;A2(﹣4,2)、B2(﹣1,1)、C3(﹣3,4);
(3)CC2==5.
20.(9分)如图,有一个长为24米的篱笆,一面有围墙(墙的最大长度为10米)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2.
(1)求S与x的函数关系式及x的取值范围.
(2)如果要围成的花圃ABCD的面积是45平方米,则AB的长为多少米?
【分析】(1)已知AB=x,BC=24﹣3x,则y=﹣3x2+24x.易求x的取值范围.
(2)当y=45时,根据实际情况求出x的值即可.
【解答】解:(1)S=(24﹣3x)x=24x﹣3x2;
又∵x>0,且10≥24﹣3x>x,
∴≤x<6;
(2)依题意有45=24x﹣3x2,
x=5或x=3;
若x=3,则AB=3m,则BC=15m>10m,舍去.
答:AB的长为5米.
21.(9分)阅读下面的例题:
解方程:x2﹣|x|﹣2=0
解:(1)当x≥0时,原方程化为x2﹣x﹣2=0,解得:x1=2,x2=﹣1(不合题意,舍去).
(2)当x<0时,原方程化为x2+x﹣2=0,解得:x1=1(不合题意,舍去),x2=﹣2
∴原方程的根是x1=2,x2=﹣2.
请参照例题解方程x2﹣|x﹣3|﹣3=0,则此方程的根是 x1=﹣3,x2=2 .
【分析】当绝对值内的数不小于0时,可直接去掉绝对值,而当绝对值内的数为负数时,去绝对值时,绝对值内的数要变为原来的相反数.本题要求参照例题解题,要先对x的值进行讨论,再去除绝对值将原式化简.
【解答】解:(1)当x≥3时,原方程化为x2﹣(x﹣3)﹣3=0,
即x2﹣x=0
解得x1=0(不合题意,舍去),x2=1(不合题意,舍去);
(2)当x<3时,原方程化为x2+x﹣3﹣3=0
即x2+x﹣6=0,
解得x1=﹣3,x2=2.
所以原方程的根是x1=﹣3,x2=2.
22.(10分)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加,某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.并指出该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(2)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
【分析】(1)根据“总利润=单件利润×销售量”得出函数解析式并配方成顶点式,即可得函数最值;
(2)根据题意得出关于x的方程,解之可得x的值,根据“销售价不高于每千克28元”取舍即可.
【解答】解:(1)根据题意得,w=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∴当x=30时,每天的利润最大,最大利润为200元;
(2)令﹣2(x﹣30)2+200=150,
解得:x=35或x=25,
∵这种产品的销售价不高于每千克28元,
∴x=25,
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
23.(12分)如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
【分析】(1)由抛物线的对称轴及点B的坐标可求出点A的坐标,由点A,B,C的坐标,利用待定系数法即可求出二次函数的表达式;
(2)连接BC,交直线x=﹣1于点M,此时△ACM周长最短,由点B,C的坐标,利用待定系数法可求出直线BC的函数表达式,再利用一次函数图象上点的坐标特征即可求出点M的坐标;
(3)设点P的坐标为(﹣1,m),结合点B,C的坐标可得出PB2,PC2,BC2的值,分∠BCP=90°,∠CBP=90°,∠BPC=90°三种情况考虑,①当∠BCP=90°时,利用勾股定理可得出关于m的一元一次方程,解之可得出m的值,进而可得出点P的坐标;②当∠CBP=90°时,利用勾股定理可得出关于m的一元一次方程,解之可得出m的值,进而可得出点P的坐标;③当∠BPC=90°时,利用勾股定理可得出关于m的一元二次方程,解之可得出m的值,进而可得出点P的坐标.综上,此题得解.
【解答】解:(1)∵二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,点B的坐标为(﹣3,0),
∴点A的坐标为(1,0).
将A(1,0),B(﹣3,0),C(0,3)代入y=ax2+bx+c,得:,
解得:,
∴二次函数的表达式为y=﹣x2﹣2x+3.
(2)连接BC,交直线x=﹣1于点M,如图1所示.
∵点A,B关于直线x=﹣1对称,
∴AM=BM.
∵点B,C,M三点共线,
∴此时AM+CM取最小值,最小值为BC.
设直线BC的函数表达式为y=kx+d(k≠0),
将B(﹣3,0),C(0,3)代入y=kx+d,得:,
解得:,
∴直线BC的函数表达式为y=x+3.
当x=﹣1时,y=x+3=2,
∴当点M的坐标为(﹣1,2)时,△ACM周长最短.
(3)设点P的坐标为(﹣1,m),
∵点B的坐标为(﹣3,0),点C的坐标为(0,3),
∴PB2=[﹣3﹣(﹣1)]2+(0﹣m)2=m2+4,PC2=[0﹣(﹣1)]2+(3﹣m)2=m2﹣6m+10,BC2=[0﹣(﹣3)]2+(3﹣0)2=18.
分三种情况考虑(如图2):
①当∠BCP=90°时,BC2+PC2=PB2,
∴18+m2﹣6m+10=m2+4,
解得:m=4,
∴点P的坐标为(﹣1,4);
②当∠CBP=90°时,BC2+PB2=PC2,
∴18+m2+4=m2﹣6m+10,
解得:m=﹣2,
∴点P的坐标为(﹣1,﹣2);
③当∠BPC=90°时,PB2+PC2=BC2,
∴m2+4+m2﹣6m+10=18,
整理得:m2﹣3m﹣2=0,
解得:m1=,m2=,
∴点P的坐标为(﹣1,)或(﹣1,).
综上所述:使△BPC为直角三角形时点P的坐标为(﹣1,﹣2),(﹣1,),(﹣1,)或(﹣1,4).
河南省安阳市汤阴县2024届九年级上学期第一次月考数学试卷(含解析): 这是一份河南省安阳市汤阴县2024届九年级上学期第一次月考数学试卷(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年河南省安阳市汤阴县部分学校九年级(上)期中数学试卷(含解析): 这是一份2023-2024学年河南省安阳市汤阴县部分学校九年级(上)期中数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
河南省安阳市汤阴县部分学校2023-2024学年九年级上学期期中数学试题: 这是一份河南省安阳市汤阴县部分学校2023-2024学年九年级上学期期中数学试题,共7页。试卷主要包含了11,5元,则每天可多售出20瓶.等内容,欢迎下载使用。












