

2021-2022学年浙江省杭州市上城区九年级(上)期中数学试卷 解析版
展开2021-2022学年浙江省杭州市上城区九年级(上)期中数学试卷
一.选择题:(每题3分,共10题,共30分)
1.(3分)下列函数关系式中,y是x的二次函数是( )
A.y=ax2+bx+c B.y=x2+
C.y=x2+2x+5 D.y=(3x+2)(4x﹣3)﹣12x2
2.(3分)某班从甲、乙、丙、丁四位选手中随机选取一人参加校乒乓球比赛,恰好选中甲选手的概率是( )
A. B. C. D.
3.(3分)如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是( )
A.80° B.100° C.110° D.120°
4.(3分)如果=,那么的值为( )
A. B. C. D.
5.(3分)在平面直角坐标系中,已知点P的坐标为(6,8),若以点P为圆心,12为半径作圆,则坐标原点O与⊙P的位置关系是( )
A.点O在⊙P内 B.点O在⊙P上 C.点O在⊙P外 D.无法确定
6.(3分)在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确的是( )
A.AE=BE B.= C.CE=EO D.=
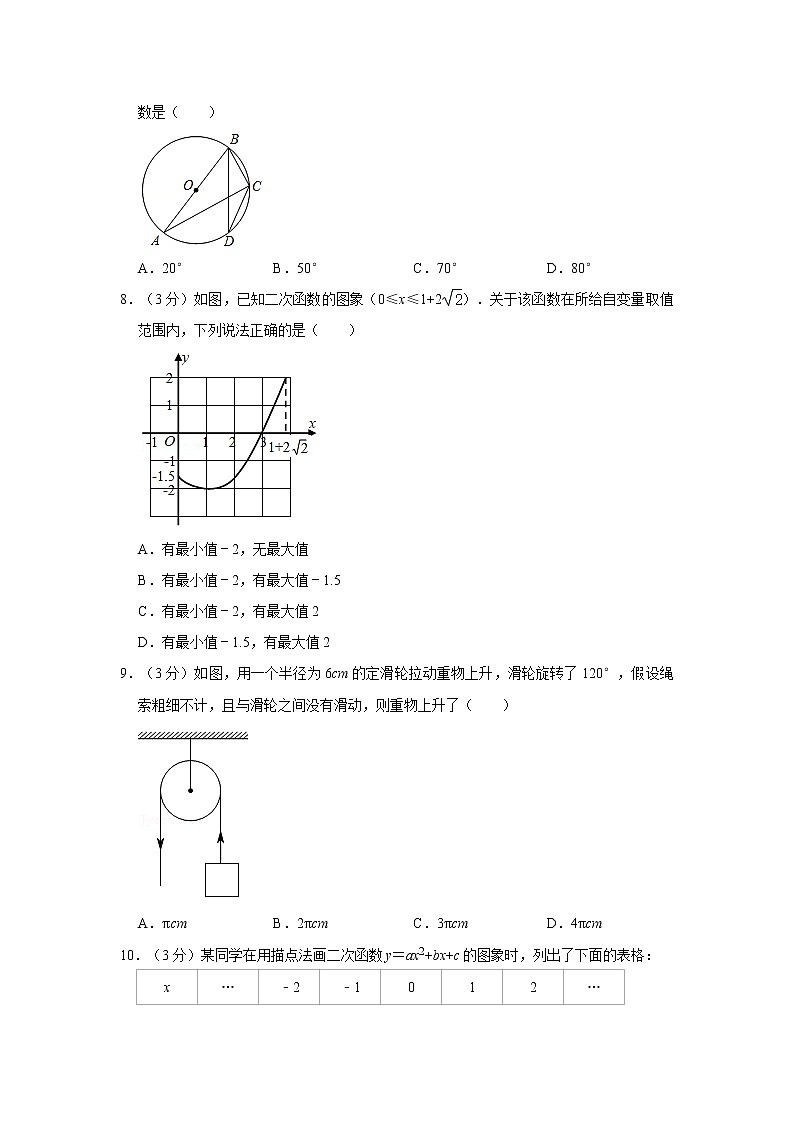
7.(3分)如图,AB是⊙O的直径,点C、D在⊙O上,且∠BDC=20°,则∠ABC的度数是( )
A.20° B.50° C.70° D.80°
8.(3分)如图,已知二次函数的图象(0≤x≤1+2).关于该函数在所给自变量取值范围内,下列说法正确的是( )
A.有最小值﹣2,无最大值
B.有最小值﹣2,有最大值﹣1.5
C.有最小值﹣2,有最大值2
D.有最小值﹣1.5,有最大值2
9.(3分)如图,用一个半径为6cm的定滑轮拉动重物上升,滑轮旋转了120°,假设绳索粗细不计,且与滑轮之间没有滑动,则重物上升了( )
A.πcm B.2πcm C.3πcm D.4πcm
10.(3分)某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣11 B.﹣5 C.2 D.﹣2
二.填空题:(每题4分,共6题,共24分)
11.(4分)将抛物线y=﹣x2+2向右平移2个单位,再向下平移3个单位,得到抛物线的解析式为 .
12.(4分)如图,两条直线被三条平行直线所截,DE=2,EF=3,AB=1,则AC= .
13.(4分)技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 .(结果要求保留两位小数)
14.(4分)若一个扇形的弧长为π,半径为2,则该扇形的面积为 ;若一个正多边形的外角为120度,则这个正多边形是正 边形.
15.(4分)已知点P坐标为(1,1),将点P绕原点逆时针旋转45°得点P1,则点P1的坐标为 .
16.(4分)二次函数(其中m>0),下列命题:①该函数图象过(6,0);②该函数图象顶点在第三象限;③当x>3时,y随着x的增大而增大;④若当x<n时,都有y随着x的增大而减小,则.正确的序号是 .
三.解答题(共7题,共66分)
17.(6分)随着信息技术的迅猛发展,移动支付已成为一种常见的支付方式.在一次购物中,马老师和赵老师随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付.
(1)请用列表法或画树状图法,求两位老师所有可能出现的支付方式;
(2)求两位老师恰好都选择“微信”支付的概率.
18.(8分)已知:抛物线y=x2﹣4x+3.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 .
(2)在坐标系中画出此抛物线.
19.(8分)如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
20.(10分)如图,在四边形ABCD中,∠DAB=∠CBA=90°,点E为AB的中点,DE⊥CE.
(1)求证:△AED∽△BCE;
(2)若AD=3,BC=12,求线段DC的长.
21.(10分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD.
(1)求证:∠ADB=∠E;
(2)当AB=6,BE=3时,求AD的长.
22.(12分)小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=﹣x2+x+c.
(1)求y与x之间的函数表达式;
(2)求篮球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.
23.(12分)如图,在圆O中,弦AB的垂直平分线OE分别交弦AB于点N、交弦BG于点D;OE交圆O于点C、F,连接OG,OB,圆O的半径为r.
(1)若∠AGB=60°,r=2,求弦AB的长;
(2)证明:∠E=∠OBD;
(3)若D是CO中点,求EF的长(用r的代数式表示).
2021-2022学年浙江省杭州市上城区九年级(上)期中数学试卷
参考答案与试题解析
一.选择题:(每题3分,共10题,共30分)
1.(3分)下列函数关系式中,y是x的二次函数是( )
A.y=ax2+bx+c B.y=x2+
C.y=x2+2x+5 D.y=(3x+2)(4x﹣3)﹣12x2
【分析】根据二次函数的定义对各选项进行判断.
【解答】解:A.当a=0时,y=ax2+bx+c不是二次函数,所以A选项不符合题意;
B.解析式中含有分式,则y=x2+不是二次函数,所以A选项不符合题意;
C.y=x2+2x+5是二次函数,所以C选项符合题意;
D.y=(3x+2)(4x﹣3)﹣12x2=﹣x﹣6,它为一次函数,所以D选项不符合题意.
故选:C.
2.(3分)某班从甲、乙、丙、丁四位选手中随机选取一人参加校乒乓球比赛,恰好选中甲选手的概率是( )
A. B. C. D.
【分析】根据概率的意义进行计算即可.
【解答】解:一共有甲、乙、丙、丁四个人,每个人被抽到的可能性是均等的,
所以甲被抽到的概率为,
故选:A.
3.(3分)如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是( )
A.80° B.100° C.110° D.120°
【分析】根据圆内接四边形的性质得出∠A+∠C=180°,再代入求出答案即可.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠A=80°,
∴∠C=100°,
故选:B.
4.(3分)如果=,那么的值为( )
A. B. C. D.
【分析】可设a=5x,b=3x,再代入计算即可.
【解答】解:设a=5x,则b=3x,
∴==,
故选:B.
5.(3分)在平面直角坐标系中,已知点P的坐标为(6,8),若以点P为圆心,12为半径作圆,则坐标原点O与⊙P的位置关系是( )
A.点O在⊙P内 B.点O在⊙P上 C.点O在⊙P外 D.无法确定
【分析】首先求得点O与圆心P之间的距离,然后和圆的半径比较即可得到点O与圆的位置关系.
【解答】解:由勾股定理得:OP==10,
∵圆P的半径为12,10<12,
∴点O在圆P内.
故选:A.
6.(3分)在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确的是( )
A.AE=BE B.= C.CE=EO D.=
【分析】根据垂径定理,垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧得出结论.
【解答】解:由垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧知:
AE=BE,,,故A,B,D正确,
故选:C.
7.(3分)如图,AB是⊙O的直径,点C、D在⊙O上,且∠BDC=20°,则∠ABC的度数是( )
A.20° B.50° C.70° D.80°
【分析】先由圆周角定理得∠ACB=90°,∠A=∠BDC=20°,再由直角三角形的性质即可得出答案.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠A=∠BDC=20°,
∴∠ABC=90°﹣∠A=90°﹣20°=70°,
故选:C.
8.(3分)如图,已知二次函数的图象(0≤x≤1+2).关于该函数在所给自变量取值范围内,下列说法正确的是( )
A.有最小值﹣2,无最大值
B.有最小值﹣2,有最大值﹣1.5
C.有最小值﹣2,有最大值2
D.有最小值﹣1.5,有最大值2
【分析】根据图象及x的取值范围,求出最大值和最小值即可.
【解答】解:根据图象及x的取值范围,
当x=1时,y取最小值为﹣2,
当x=1+2,y取最大值为2,
∴该函数有最小值﹣2,有最大值2,
故选:C.
9.(3分)如图,用一个半径为6cm的定滑轮拉动重物上升,滑轮旋转了120°,假设绳索粗细不计,且与滑轮之间没有滑动,则重物上升了( )
A.πcm B.2πcm C.3πcm D.4πcm
【分析】利用题意得到重物上升的高度为定滑轮中120°所对应的弧长,然后根据弧长公式计算即可.
【解答】解:根据题意,重物的高度为=4π(cm).
故选:D.
10.(3分)某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣11
﹣2
1
﹣2
﹣5
…
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣11 B.﹣5 C.2 D.﹣2
【分析】根据表格中的数据和二次函数的性质可知x=0、x=1、x=﹣1对应的函数值是正确的,从而可以求得二次函数的解析式,再将x=2和x=﹣2代入解析式,即可判断哪个y值是错误的,本题得以解决.
【解答】解:由表格可得,
该二次函数的对称轴是直线x=0,经过点(﹣1,﹣2),(0,1),(1,﹣2),
∴,
解得,,
∴y=﹣3x2+1,
当x=﹣2时,y=﹣11,
当x=2时,y=﹣11,
故选:B.
二.填空题:(每题4分,共6题,共24分)
11.(4分)将抛物线y=﹣x2+2向右平移2个单位,再向下平移3个单位,得到抛物线的解析式为 y=﹣(x﹣2)2﹣1 .
【分析】根据“左加右减,上加下减”的平移规律写出平移抛物线解析式.
【解答】解:将抛物线y=﹣x2+2向右平移2个单位,再向下平移3个单位,所得到的抛物线解析式为 y=﹣(x﹣2)2+2﹣3,即y=﹣(x﹣2)2﹣1.
故答案是:y=﹣(x﹣2)2﹣1.
12.(4分)如图,两条直线被三条平行直线所截,DE=2,EF=3,AB=1,则AC= .
【分析】利用平行线分线段成比例定理解决问题即可.
【解答】解:∵l1∥l2∥l1,
∴=,
∴=,
∴BC=,
∴AC=AB+BC=1+=,
故答案为:.
13.(4分)技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为 0.99 .(结果要求保留两位小数)
【分析】根据抽检某一产品2020件,发现产品合格的频率已达到0.9911,所以估计合格件数的概率为0.99,问题得解.
【解答】解:∵抽检某一产品2020件,发现产品合格的频率已达到0.9911,
∴依此我们可以估计该产品合格的概率为0.99,
故答案为:0.99.
14.(4分)若一个扇形的弧长为π,半径为2,则该扇形的面积为 3 ;若一个正多边形的外角为120度,则这个正多边形是正 三 边形.
【分析】根据扇形的面积=•l•r,计算即可;多边形的外角和等于360°,因为所给多边形的每个外角均相等,据此即可求得正多边形的边数,进而求解.
【解答】解:由题意,S扇形=×π×2=π,
∵=3,
∴这个正多边形是正三边形.
故答案为:3,三.
15.(4分)已知点P坐标为(1,1),将点P绕原点逆时针旋转45°得点P1,则点P1的坐标为 (0,) .
【分析】利用点P的坐标特征可判断OP与y轴正方向的夹角为45°,于是可判断点P绕原点逆时针旋转45°得点P1,则点P1在y轴上,根据OP1=OP可得点P1的纵坐标.
【解答】解:如图,连接OP,
∵点P坐标为(1,1),
∴OP与y轴正方向的夹角为45°,
∴点P绕原点逆时针旋转45°得点P1,点P1在y轴上,OP1=OP==.
∴点P1的坐标为(0,).
故答案为(0,).
16.(4分)二次函数(其中m>0),下列命题:①该函数图象过(6,0);②该函数图象顶点在第三象限;③当x>3时,y随着x的增大而增大;④若当x<n时,都有y随着x的增大而减小,则.正确的序号是 ①④ .
【分析】先把二次函数化简为一般式,求得对称轴与△,再根据二次函数的性质进行判断即可.
【解答】解:∵=mx2﹣(6m+1)x+6,
∴对称轴为x=﹣=3+,△=[﹣(6m+1)]2﹣24m=(6m﹣1)2≥0,
当x=6时,y=0,
∴该函数图象过(6,0);故①正确;
∵=mx2﹣(6m+1)x+6,
∴对称轴为x=﹣=3+>0,该函数图象顶点不在第三象限,故②错误;
当x>3+时,y随x的增大而增大,故③错误;
C、当x<n时,y随x的增大而减小,即x≤3+,此选项正确;
故答案为:①④.
三.解答题(共7题,共66分)
17.(6分)随着信息技术的迅猛发展,移动支付已成为一种常见的支付方式.在一次购物中,马老师和赵老师随机从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付.
(1)请用列表法或画树状图法,求两位老师所有可能出现的支付方式;
(2)求两位老师恰好都选择“微信”支付的概率.
【分析】(1)把“微信”、“支付宝”、“银行卡”三种支付方式分别记为:A、B、C,列表可得所有结果;
(2)共有9种等可能的结果,其中马老师和赵老师恰好都选择“微信”支付的结果有1种,再由概率公式求解即可.
【解答】解:(1)把“微信”、“支付宝”、“银行卡”三种支付方式分别记为:A、B、C,
列表如下:
A
B
C
A
(A,A)
(B,A)
(C,A)
B
(A,B)
(B,B)
(C,B)
C
(A,C)
(B,C)
(C,C)
(2)共有9种等可能的结果,其中马老师和赵老师恰好都选择“微信”支付的结果有1种,
∴马老师和赵老师恰好都选择“微信”支付的概率为.
18.(8分)已知:抛物线y=x2﹣4x+3.
(1)它与x轴交点的坐标为 (3,0)、(1,0) ,与y轴交点的坐标为 (0,3) ,顶点坐标为 (2,﹣1) .
(2)在坐标系中画出此抛物线.
【分析】(1)根据抛物线的解析式,可以求得它与x轴交点的坐标、与y轴交点的坐标以及顶点坐标;
(2)根据(1)中的结果,可以画出相应的抛物线.
【解答】解:(1)∵抛物线y=x2﹣4x+3=(x﹣2)2﹣1=(x﹣3)(x﹣1),
∴该抛物的顶点坐标为(2,﹣1),当y=0时,x1=3,x2=1,当x=0时,y=3,
∴它与x轴交点的坐标为(3,0)、(1,0),与y轴交点的坐标为(0,3),顶点坐标为(2,﹣1),
故答案为:(3,0)、(1,0),(0,3),(2,﹣1);
(2)由(1)知,它与x轴交点的坐标为(3,0)、(1,0),与y轴交点的坐标为(0,3),顶点坐标为(2,﹣1),且过点(4,3),
抛物线如右图所示.
19.(8分)如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
【分析】(1)想办法证明=即可解决问题.
(2)连接OM,利用勾股定理垂径定理解决问题即可.
【解答】(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
20.(10分)如图,在四边形ABCD中,∠DAB=∠CBA=90°,点E为AB的中点,DE⊥CE.
(1)求证:△AED∽△BCE;
(2)若AD=3,BC=12,求线段DC的长.
【分析】(1)根据两角对应相等的两个三角形相似证明即可.
(2)利用相似三角形的性质以及勾股定理解决问题即可.
【解答】(1)证明:∵EC⊥DE,
∴∠DEC=90°,
∵∠DAB=∠CBA=90°,
∴∠ADE+∠AED=90°,∠AED+∠CEB=90°,
∴∠ADE=∠CEB,
∴△AED∽△BCE.
(2)∵△AED∽△BCE,
∴=,∵AE=EB,
∴AE2=AD•BC=36,
∴AE=EB=6,
∴DE2=AD2+AE2=32+62=45,EC2=BE2+BC2=62+122=180,
∴CD===15.
21.(10分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连接AD、BD.
(1)求证:∠ADB=∠E;
(2)当AB=6,BE=3时,求AD的长.
【分析】运用圆周角定理,以及平行线的性质得出角之间的关系,得出相等关系,再利用三角形相似得出比例式,从而求出AD.
【解答】(1)证明:∵AB=AC,点D在弧BC上运动,过点D作DE∥BC
∴,∠ABC=∠AED,∠ABC=∠ACB,∠ADB=∠ACB
∴∠ADB=∠E
(2)解:∵∠ABC=∠AED,∠ABC=∠ACB,∠ADB=∠ACB
∴∠ADB=∠E,∠BAD=∠BAD,
∴△ABD∽△ADE,
AB=6,BE=3,
∴AD2=6×9,
AD=3,
∴AD的长为3.
22.(12分)小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=﹣x2+x+c.
(1)求y与x之间的函数表达式;
(2)求篮球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.
【分析】(1)直接利用P点坐标得出c的值即可;
(2)求出二次函数的顶点坐标进而得出答案;
(3)令y=2.5,进而得出答案x的值,即可得出答案.
【解答】解:(1)∵OP=1,
∴当x=0时,y=1,代入y=x2+x+c,
解得:c=1,
∴y与x的函数表达式为y=﹣x2+x+1;
(2)y=﹣x2+x+1,
=x2﹣8x)+1,
=(x﹣4)2+3,
当x=4时,y有最大值3,
故篮球在运动的过程中离地面的最大高度为3m;
(3)令y=2.5,则有﹣(x﹣4)2+3=2.5,
解得x1=2,x2=6,
根据题意可知x1=2不合题意,应舍去故小亮离小明的最短距离为6m.
23.(12分)如图,在圆O中,弦AB的垂直平分线OE分别交弦AB于点N、交弦BG于点D;OE交圆O于点C、F,连接OG,OB,圆O的半径为r.
(1)若∠AGB=60°,r=2,求弦AB的长;
(2)证明:∠E=∠OBD;
(3)若D是CO中点,求EF的长(用r的代数式表示).
【分析】(1)设OF交AB于N,连接AO,根据圆的性质与三角函数计算可得答案;
(2)想办法证明∠E=∠OBD,∠OGB=∠OBD可得结论;
(3)证明△OGD∽△OEG,相似三角形的性质可得答案.
【解答】(1)解:设OF交AB于N,连接AO,
∴∠AOB=2∠AGB=120°,
∵OA=OB,OA⊥AB,
∴AN=BN=AB,
∴∠AOB=∠BON=∠AOB=60°,∠ONB=∠ONA=90°,
∴sin∠AON==,
∴AN=×2=,
∴AB=2AN=2.
(2)证明:∵∠AOB=2∠AGB,∠AON=∠BON=∠AOB,
∴∠BON=∠AGB,
∴∠EGD=∠DOB,
∵∠EDG=∠BDO,
∴∠E=∠OBD,
∵OG=OB,
∴∠OGB=∠OBG,
∴∠E=∠OGB.
(3)解:∵D是CO中点,
∴OD=OC=,
∵∠OGD=∠E,∠GOD=∠EOG,
∴△OGD∽△OEG,
∴=,即=,
∴OE=2r,
∵OF=r,
∴EF=OE+OF=3r.
2022-2023学年浙江省杭州市上城区建兰中学九年级(上)期中数学试卷(含解析): 这是一份2022-2023学年浙江省杭州市上城区建兰中学九年级(上)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年浙江省杭州市上城区九年级(上)期末数学试卷(学生版+解析版): 这是一份2021-2022学年浙江省杭州市上城区九年级(上)期末数学试卷(学生版+解析版),共22页。
2021-2022学年浙江省杭州市上城区九年级(上)期末数学试卷 word,解析版: 这是一份2021-2022学年浙江省杭州市上城区九年级(上)期末数学试卷 word,解析版,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












