安徽省合肥市2021-2022学年八年级上学期期中数学试卷（word版 含答案）

这是一份安徽省合肥市2021-2022学年八年级上学期期中数学试卷（word版 含答案），共20页。试卷主要包含了选择题，填空题.，解答题.等内容，欢迎下载使用。
2021-2022学年八年级第一学期期中数学试卷
一、选择题（每小题3分，共30分）
1．点A（3，2）关于x轴的对称点为B，则点B的坐标为（　　）
A．（3，2） B．（﹣3，﹣2） C．（﹣3，2） D．（3，﹣2）
2．若三角形的两条边长分别为6cm和10cm，则它的第三边长不可能为（　　）
A．5cm B．8cm C．10cm D．17cm
3．函数y＝中，自变量x的取值范围是（　　）
A．x≤1 B．x≥1 C．x＜1且x≠0 D．x≤1且x≠0
4．已知一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3，1），则关于x的方程ax﹣1＝mx+4的解是（　　）
A．x＝﹣1 B．x＝1 C．x＝3 D．x＝4
5．若直线y＝k1x+1与y＝k2x﹣4的交点在x轴上，那么等于（　　）
A．4 B．﹣4 C． D．
6．给定下列条件，不能判定三角形是直角三角形的是（　　）
A．∠A：∠B：∠C＝1：2：3 B．∠A﹣∠C＝∠B
C．∠A＝∠B＝2∠C D．∠A＝∠B＝∠C
7．现有若干个三角形，在所有的内角中，有5个直角，3个钝角，25个锐角，则在这些三角形中锐角三角形的个数是（　　）
A．3 B．4或5 C．6或7 D．8
8．已知一次函数y＝kx+3的图象经过点A，且y随x的增大而减小，则点A的坐标可以是（　　）
A．（﹣1，2） B．（1，﹣2） C．（2，3） D．（3，4）
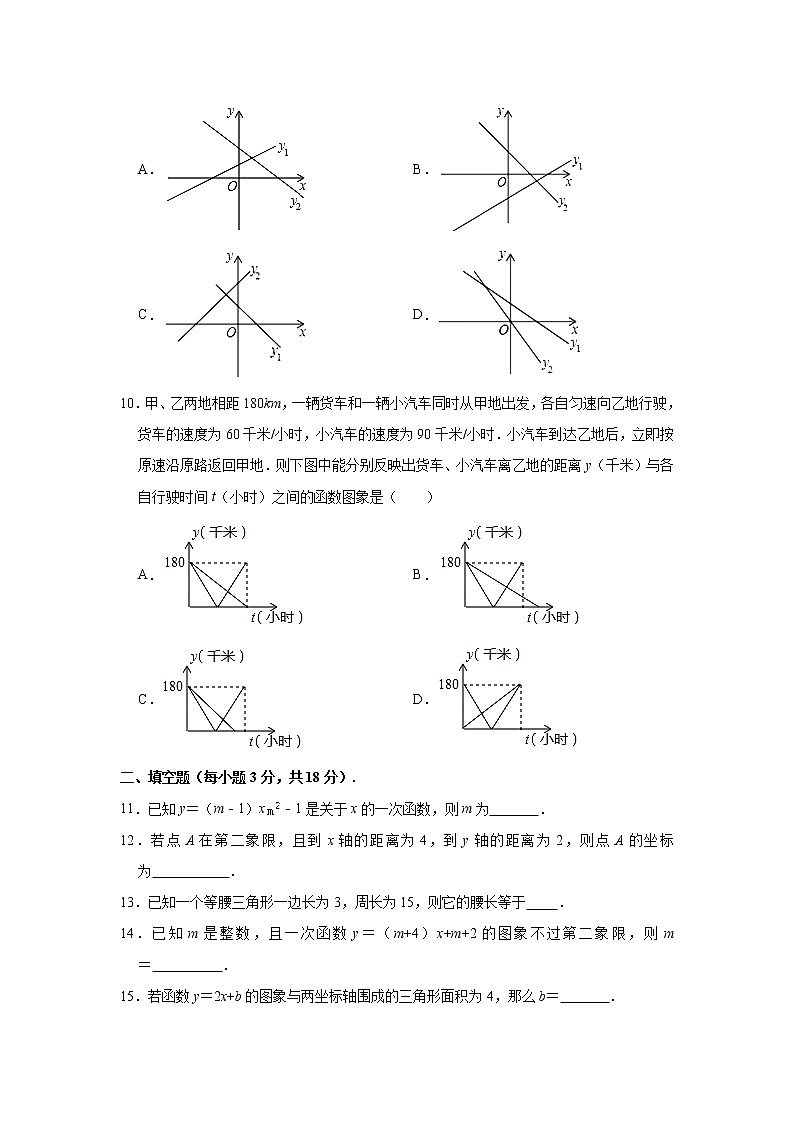
9．已知两个一次函数y1＝ax+b与y2＝bx+a，它们在同一平面直角坐标系中的图象可能是下列选项中的（　　）
A． B．
C． D．
10．甲、乙两地相距180km，一辆货车和一辆小汽车同时从甲地出发，各自匀速向乙地行驶，货车的速度为60千米/小时，小汽车的速度为90千米/小时．小汽车到达乙地后，立即按原速沿原路返回甲地．则下图中能分别反映出货车、小汽车离乙地的距离y（千米）与各自行驶时间t（小时）之间的函数图象是（　　）
A． B．
C． D．
二、填空题（每小题3分，共18分）.
11．已知y＝（m﹣1）x﹣1是关于x的一次函数，则m为　 　．
12．若点A在第二象限，且到x轴的距离为4，到y轴的距离为2，则点A的坐标为　 　．
13．已知一个等腰三角形一边长为3，周长为15，则它的腰长等于　 　．
14．已知m是整数，且一次函数y＝（m+4）x+m+2的图象不过第二象限，则m＝　 　．
15．若函数y＝2x+b的图象与两坐标轴围成的三角形面积为4，那么b＝　 　．
16．如图，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D．若∠A′DC＝90°，则∠A＝　 　．

三、解答题.
17．将三角形ABC向右平移3个单位长度，再向下平移2个单位长度，得到对应的三角形A1B1C1．
（1）画出三角形A1B1C1，并写出点A1，B1，C1的坐标；
（2）求三角形A1B1C1的面积．

18．直线y＝kx+b与直线y＝5﹣4x平行，且与直线y＝﹣3（x﹣6）相交，交点在y轴上，求直线y＝kx+b对应的函数解析式．
19．如图，在直角坐标系中，直线l1：y＝kx﹣1与直线l2：y＝x+2交于点A（m，1）．
（1）求m的值；
（2）设直线l1，l2分别与y轴交于点B，C，求△ABC的面积；
（3）结合图象，直接写出不等式0＜kx﹣1＜x+2的解集．

20．（1）如图1，在△ABC纸片中，点D在边AC上，点E在边AB上，沿DE折叠，当点A落在CD上时，∠DAE与∠1之间有一种数量关系保持不变，请找出这种数量关系并说明理由；
（2）若折成图2时，即点A落在△ABC内时，请找出∠DAE与∠1，∠2之间的关系式并说明理由．

21．为了做好新冠的个人防疫，小明妈妈联合班级其他同学的家长去药店团购口罩．口罩原来一包是20元，由于家长们购买的数量比较多，药店老板决定给他们优惠，
方式如下：
方式一：每包口罩打九折；
方式二：如果购买的口罩不超过40包，则口罩按原价销售，如果购买的口罩超过40包，则超出的部分打八折销售．
设大家一共需要团购口罩x包，
（1）口罩的总费用为y元，请分别求出两种方式y与x的关系式；
（2）已知每位家长为孩子都准备5包口罩，小明妈妈根据联合家长的人数如何选择优惠方式？
22．已知△ABC的面积是60，请完成下列问题：
（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积 　 　△ACD的面积（填“＞”“＜”或“＝”）；
（2）如图2，若CD，BE分别是△ABC的AB，AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD＝DB，得S△ADO＝S△BDO；同理S△CEO＝S△AEO．设S△BDO＝x，S△CEO＝y，则S△ADO＝x，S△AEO＝y．由题意得S△ABE＝S△ABC＝30，S△ADC＝S△ABC＝30，故可列方程组，解得x，y分别为 　 　，从而得到四边形ADOE的面积为 　 　；
（3）如图3，已知AD：DB＝1：3，CE：AE＝1：2，请你计算四边形ADOE的面积，并说明理由．



参考答案
一、选择题（每小题3分，共30分）
1．点A（3，2）关于x轴的对称点为B，则点B的坐标为（　　）
A．（3，2） B．（﹣3，﹣2） C．（﹣3，2） D．（3，﹣2）
【分析】利用关于x轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数，即可得出点B的坐标．
解：∵点A（3，2）关于x轴的对称点为B，
∴B（3，﹣2），
故选：D．
2．若三角形的两条边长分别为6cm和10cm，则它的第三边长不可能为（　　）
A．5cm B．8cm C．10cm D．17cm
【分析】直接利用三角形三边关系得出第三边的取值范围，进而得出答案．
解：∵三角形的两条边长分别为6cm和10cm，
∴第三边长的取值范围是：4＜x＜16，
∴它的第三边长不可能为：17cm．
故选：D．
3．函数y＝中，自变量x的取值范围是（　　）
A．x≤1 B．x≥1 C．x＜1且x≠0 D．x≤1且x≠0
【分析】根据二次根式的性质和分式的意义，被开方数大于等于0，分母不等于0，列不等式组求解．
解：根据题意得：
解得：x≤1且x≠0．
故选：D．
4．已知一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3，1），则关于x的方程ax﹣1＝mx+4的解是（　　）
A．x＝﹣1 B．x＝1 C．x＝3 D．x＝4
【分析】根据方程的解即为函数图象的交点横坐标解答．
解：∵一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3，1），
∴ax﹣1＝mx+4的解是x＝3．
故选：C．
5．若直线y＝k1x+1与y＝k2x﹣4的交点在x轴上，那么等于（　　）
A．4 B．﹣4 C． D．
【分析】分别求出两直线与x轴的交点的横坐标，然后列出方程整理即可得解．
解：令y＝0，则k1x+1＝0，
解得x＝﹣，
k2x﹣4＝0，
解得x＝，
∵两直线交点在x轴上，
∴﹣＝，
∴＝﹣．
故选：D．
6．给定下列条件，不能判定三角形是直角三角形的是（　　）
A．∠A：∠B：∠C＝1：2：3 B．∠A﹣∠C＝∠B
C．∠A＝∠B＝2∠C D．∠A＝∠B＝∠C
【分析】根据三角形的内角和等于180°求出三角形的最大角，进而得出结论．
解：A、设∠A＝x，则∠B＝2x，∠C＝3x，
∴x+2x+3x＝180°，
解得：x＝30°，
∴最大角∠C＝3×30°＝90°，
∴三角形是直角三角形，选项A不符合题意；
B、∵∠A﹣∠C＝∠B，
∴∠A＝∠B+∠C，
又∵∠A+∠B+∠C＝180°，
∴∠A＝180°÷2＝90°，
∴三角形是直角三角形，选项B不符合题意；
C、设∠C＝y，则∠A＝2y，∠B＝2y，
∴y+2y+2y＝180°，
解得：y＝36°，
∴最大角∠B＝2×36°＝72°，
∴三角形不是直角三角形，选项C符合题意；
D、设∠A＝z，则∠B＝z，∠C＝2z，
∴z+z+2z＝180°，
解得：z＝45°，
∴最大角∠C＝2×45°＝90°，
∴三角形是直角三角形，选项D不符合题意．
故选：C．
7．现有若干个三角形，在所有的内角中，有5个直角，3个钝角，25个锐角，则在这些三角形中锐角三角形的个数是（　　）
A．3 B．4或5 C．6或7 D．8
【分析】根据三角形的定义，先得出三角形的个数．再根据三角形的分类，得出锐角三角形的个数．
解：由题意得：若干个三角形，在所有的内角中，有5个直角，3个钝角，25个锐角时，
∴共有33÷3＝11个三角形；
又三角形中，最多有一个直角或最多有一个钝角，显然11个三角形中，有5个直角三角形和3个钝角三角形；
故还有11﹣5﹣3＝3个锐角三角形．
故选：A．
8．已知一次函数y＝kx+3的图象经过点A，且y随x的增大而减小，则点A的坐标可以是（　　）
A．（﹣1，2） B．（1，﹣2） C．（2，3） D．（3，4）
【分析】由点A的坐标，利用一次函数图象上点的坐标特征求出k值，结合y随x的增大而减小即可确定结论．
解：A、当点A的坐标为（﹣1，2）时，﹣k+3＝2，
解得：k＝1＞0，
∴y随x的增大而增大，选项A不符合题意；
B、当点A的坐标为（1，﹣2）时，k+3＝﹣2，
解得：k＝﹣5＜0，
∴y随x的增大而减小，选项B符合题意；
C、当点A的坐标为（2，3）时，2k+3＝3，
解得：k＝0，选项C不符合题意；
D、当点A的坐标为（3，4）时，3k+3＝4，
解得：k＝＞0，
∴y随x的增大而增大，选项D不符合题意．
故选：B．
9．已知两个一次函数y1＝ax+b与y2＝bx+a，它们在同一平面直角坐标系中的图象可能是下列选项中的（　　）
A． B．
C． D．
【分析】先由一次函数y1＝ax+b图象得到字母系数的符号，再与一次函数y2＝bx+a的图象相比较看是否一致．
解：A、∵一次函数y1＝ax+b的图象经过一三四象限，
∴a＞0，b＞0；
由一次函数y2＝bx+a图象可知，b＜0，a＞0，两结论矛盾，故错误；
B、∵一次函数y1＝ax+b的图象经过一三四象限，
∴a＞0，b＜0；
由y2的图象可知，a＞0，b＜0，两结论不矛盾，故正确；
C、∵一次函数y1＝ax+b的图象经过一二四象限，
∴a＜0，b＞0；
由y2的图象可知，a＞0，b＞0，两结论矛盾，故错误；
D、∵一次函数y1＝ax+b的图象经过一二四象限，
∴a＜0，b＞0；
由y2的图象可知，a＜0，b＝0，两结论相矛盾，故错误．
故选：B．
10．甲、乙两地相距180km，一辆货车和一辆小汽车同时从甲地出发，各自匀速向乙地行驶，货车的速度为60千米/小时，小汽车的速度为90千米/小时．小汽车到达乙地后，立即按原速沿原路返回甲地．则下图中能分别反映出货车、小汽车离乙地的距离y（千米）与各自行驶时间t（小时）之间的函数图象是（　　）
A． B．
C． D．
【分析】根据出发前都距离乙地180千米，出发两小时小汽车到达乙地距离变为零，再经过两小时小汽车又返回甲地距离又为180千米；经过三小时，货车到达乙地距离变为零，故而得出答案．
解：由题意得出发前都距离乙地180千米，出发两小时小汽车到达乙地距离变为零，再经过两小时小汽车又返回甲地距离又为180千米，经过三小时，货车到达乙地距离变为零，故C符合题意，
故选：C．
二、填空题（每小题3分，共18分）.
11．已知y＝（m﹣1）x﹣1是关于x的一次函数，则m为　﹣1　．
【分析】根据一次函数定义可得m2＝1，且m﹣1≠0，再解出m的值即可．
解：由题意得：m2＝1，且m﹣1≠0，
解得：m＝﹣1，
故答案为：﹣1．
12．若点A在第二象限，且到x轴的距离为4，到y轴的距离为2，则点A的坐标为　（﹣2，4）　．
【分析】根据第二象限内点的横坐标是负数，纵坐标是正数，点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度解答即可．
解：∵点A在第二象限，且A点到x轴的距离为4，
∴点A的纵坐标为4，
∵点A到y轴的距离为2，
∴点A的横坐标是﹣2，
∴点A的坐标为（﹣2，4）．
故答案为：（﹣2，4）．
13．已知一个等腰三角形一边长为3，周长为15，则它的腰长等于　6　．
【分析】分别从腰长为3与底边长为3，去分析求解即可求得答案．
解：若腰长为3，则底边长为：15﹣3﹣3＝9，
∵3+3＜9，
∴不能组成三角形，舍去；
若底边长为3，则腰长为：＝6；
∴该等腰三角形的腰长为：6．
故答案为：6．
14．已知m是整数，且一次函数y＝（m+4）x+m+2的图象不过第二象限，则m＝　﹣3或﹣2　．
【分析】由于一次函数y＝（m+4）x+m+2的图象不过第二象限，则得到，然后解不等式即可m的值．
解：∵一次函数y＝（m+4）x+m+2的图象不过第二象限，
∴，
解得﹣4＜m≤﹣2，
而m是整数，
则m＝﹣3或﹣2．
故填空答案：﹣3或﹣2．
15．若函数y＝2x+b的图象与两坐标轴围成的三角形面积为4，那么b＝　±4　．
【分析】利用一次函数y＝2x+b的图象与x轴交点和与y轴交点的特点求出坐标，以及图象与坐标轴所围成的三角形是直角三角形求解．
解：∵当y＝0时，0＝2x+b，
∴x＝﹣；
当x＝0时，y＝b，
∴一次函数y＝2x+b的图象与坐标轴所围成的三角形面积：×|﹣|×|b|＝4，
解得b＝±4，
故答案为：±4．
16．如图，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D．若∠A′DC＝90°，则∠A＝　55°　．

【分析】根据题意得出∠ACA′＝35°，则∠A′＝90°﹣35°＝55°，即可得出∠A的度数．
解：∵把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC于点D，∠A′DC＝90°，
∴∠ACA′＝35°，则∠A′＝90°﹣35°＝55°，
则∠A＝∠A′＝55°．
故答案为：55°．
三、解答题.
17．将三角形ABC向右平移3个单位长度，再向下平移2个单位长度，得到对应的三角形A1B1C1．
（1）画出三角形A1B1C1，并写出点A1，B1，C1的坐标；
（2）求三角形A1B1C1的面积．

【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；
（2）直接利用△A1B1C1所在矩形面积减去周围三角形面积进而得出答案．
解：（1）如图所示：△A1B1C1，即为所求；
A1（2，2），B1（﹣1，﹣3），C1（4，﹣1）；

（2）三角形A1B1C1的面积为：5×5﹣×3×5﹣×2×3﹣×2×5＝9.5．

18．直线y＝kx+b与直线y＝5﹣4x平行，且与直线y＝﹣3（x﹣6）相交，交点在y轴上，求直线y＝kx+b对应的函数解析式．
【分析】因为一次函数y＝kx+b的图象与直线y＝5﹣4x平行，可知k＝﹣4，进而求出直线y＝﹣3（x﹣6）与y轴交于点（0，18），将点（0，18）代入一次函数y＝kx+b中求b即可．
解：∵直线y＝kx+b与直线y＝5﹣4x平行，
∴k＝﹣4，
又∵与直线y＝﹣3（x﹣6）的交点在y轴上，
∴直线过（0，18）点，
∴直线的解析式为y＝﹣4x+18．
19．如图，在直角坐标系中，直线l1：y＝kx﹣1与直线l2：y＝x+2交于点A（m，1）．
（1）求m的值；
（2）设直线l1，l2分别与y轴交于点B，C，求△ABC的面积；
（3）结合图象，直接写出不等式0＜kx﹣1＜x+2的解集．

【分析】（1）先把A（m，1）代入y＝x+2，求出m的值；
（2）把A点坐标代入y＝kx﹣1，求出k，即可得到直线l1的表达式，然后求出B、C两点坐标，再根据三角形的面积个数即可求解；
（3）找出直线l1落在直线l2下方且在x轴上方的部分对应的自变量的取值范围即可．
解：（1）∵直线l2：y＝x+2过点A（m，1）．
∴1＝m+2，解得m＝﹣2；
（2）∵直线l1：y＝kx﹣1过点A（﹣2，1），
∴1＝﹣2k﹣1，解得k＝﹣1，
∴直线l1的表达式为y＝﹣x﹣1，
∴B（0，﹣1），
由直线l2：y＝x+2可知C（0，2），
∴BC＝3，
∴S△ABC＝×3×2＝3；

（3）在直线l1：y＝﹣x﹣1中，令y＝0，则x＝﹣1，
观察图象可知，不等式0＜kx﹣1＜x+2的解集是﹣2＜x＜﹣1．
20．（1）如图1，在△ABC纸片中，点D在边AC上，点E在边AB上，沿DE折叠，当点A落在CD上时，∠DAE与∠1之间有一种数量关系保持不变，请找出这种数量关系并说明理由；
（2）若折成图2时，即点A落在△ABC内时，请找出∠DAE与∠1，∠2之间的关系式并说明理由．

【分析】（1）如图1中，延长BE交CD于R．利用翻折不变以及三角形我记得性质解决问题即可．
（2）如图2中，延长BE交CD的延长线于T，连接AT．利用翻折不变性以及三角形外角的性质解决问题即可．
解：（1）结论：∠1＝2∠DAE．
理由：如图1中，延长BE交CD于R．

由翻折可知，∠EAD＝∠R，
∵∠1＝∠EAD+∠R，
∴∠1＝2∠EAD．

（2）结论：∠1+∠2＝2∠EAD．
理由：如图2中，延长BE交CD的延长线于T，连接AT．

由翻折可知，∠EAD＝∠ETD，
∵∠1＝∠EAT+∠ETA，∠2＝∠DAT+∠DTA，
∴∠1+∠2＝∠EAT+∠ETA+∠DAT+∠DTA＝∠EAD+∠ETD＝2∠EAD．
21．为了做好新冠的个人防疫，小明妈妈联合班级其他同学的家长去药店团购口罩．口罩原来一包是20元，由于家长们购买的数量比较多，药店老板决定给他们优惠，
方式如下：
方式一：每包口罩打九折；
方式二：如果购买的口罩不超过40包，则口罩按原价销售，如果购买的口罩超过40包，则超出的部分打八折销售．
设大家一共需要团购口罩x包，
（1）口罩的总费用为y元，请分别求出两种方式y与x的关系式；
（2）已知每位家长为孩子都准备5包口罩，小明妈妈根据联合家长的人数如何选择优惠方式？
【分析】（1）根据题意，可以分别写出方式一和方式二中y与x的函数关系式；
（2）根据题意，可以计算出当x为多少时，两种方式花费一样多，从而可以得到小明妈妈根据联合家长的人数如何选择优惠方式．
解：（1）由题意可得，
方式一：y与x的函数关系式为y＝20×0.9x＝18x；
方式二：当0≤x≤40时，y＝20x，
当x＞40时，y＝20×40+20×0.8（x﹣40）＝16x+160，
由上可得，y＝；
（2）由题意可得，当0≤x≤40时，选择方式一，
当x＞40时，令18x＝16x+160，解得x＝80，
∵80÷5＝16，
∴当家长人数小于16时，选择方式一，
当家长人数等于16时，选择方式一和方式二一样，
当家长人数大于16时，选择方式二．
22．已知△ABC的面积是60，请完成下列问题：
（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积 　＝　△ACD的面积（填“＞”“＜”或“＝”）；
（2）如图2，若CD，BE分别是△ABC的AB，AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD＝DB，得S△ADO＝S△BDO；同理S△CEO＝S△AEO．设S△BDO＝x，S△CEO＝y，则S△ADO＝x，S△AEO＝y．由题意得S△ABE＝S△ABC＝30，S△ADC＝S△ABC＝30，故可列方程组，解得x，y分别为 　　，从而得到四边形ADOE的面积为 　20　；
（3）如图3，已知AD：DB＝1：3，CE：AE＝1：2，请你计算四边形ADOE的面积，并说明理由．

【分析】（1）利用三角形的面积公式计算即可得出结论；
（2）利用题干所给解答方法解答即可；
（3）连接AO，利用（2）中的方法，设S△ADO＝x，S△CEO＝y，则S△BDO＝3x，S△AEO＝2y，利用已知条件列出方程组，解方程组即可得出结论．
解：（1）过点A作AE⊥BC于点E，如图1，

∵AD是△ABC的BC边上的中线，
∴BD＝DC．
∵S△ABD＝，S△ADC＝CD•AE，
∴S△ABD＝S△ACD．
故答案为：＝．
（2）连接AO，如图2，

∵AD＝DB，
由（1）得：S△ADO＝S△BDO，
同理：S△CEO＝S△AEO，
设S△BDO＝x，S△CEO＝y，则S△ADO＝x，S△AEO＝y，
∵CD、BE分别是△ABC的AB、AC边上的中线，
∴S△ABE＝S△BEC＝S△ABC＝30，S△ADC＝S△BDC＝S△ABC＝30，
∵S△ABE＝S△BDC+S四边形ADOE，S△ADC＝S△CEO+S四边形ADOE，
∴可列方程组，解得，
∴S△ADO＝10，S△AEO＝10，
∴S四边形ADOE＝S△ADO+S△AEO＝20，
故答案为：；20；
（3）如图，连接AO，

∵AD：DB＝1：3，
∴，
又∵CE：AE＝1：2，
∴，
设S△ADO＝x，S△CEO＝y，则S△BDO＝3x，S△AEO＝2y，
由题意得，．
故可列方程组，解得，
所以S四边形ADOE＝S△ADO+S△AEO＝x+2y＝13．