北京市东城区2021-2022学年上学期九年级期中考试数学试卷（word版 含答案）

这是一份北京市东城区2021-2022学年上学期九年级期中考试数学试卷（word版 含答案），共16页。试卷主要包含了函数的最小值是，下列方程中，无实数根的方程是等内容，欢迎下载使用。

2021-2022学年度
九年级数学期中测试 2021年11月
考
生
须
知
1.本试卷共8页，共三道大题，28道小题，满分100分。考试时间120分钟。
2.在试卷、答题卡的规定位置认真填写班级、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。
4.选择题、作图题在答题卡上用2B铅笔作答，其他试题请用黑色字迹签字笔在答题卡上完成作答。
5.考试结束，请将考试材料按监考教师要求交回。
一、 选择题(共16分，每题2分)第1-8题均有四个选项，符合题意的选项只有一个。
1．围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是

A． B． C． D．
2．函数的最小值是
A．1 B．－1 C．2 D．－2
3．若关于x的方程的一个根是-1，则a的值是
A．1 B．-1 C． D．-3
4．下列方程中，无实数根的方程是
A. B. C. D.
5．直径为10分米的圆柱形排水管，截面如图所示．若管内有积水（阴影部分），
水面宽AB为8分米，则积水的最大深度CD为
A．2分米 B．3分米　　　C．4分米 D．5分米





5题 6题
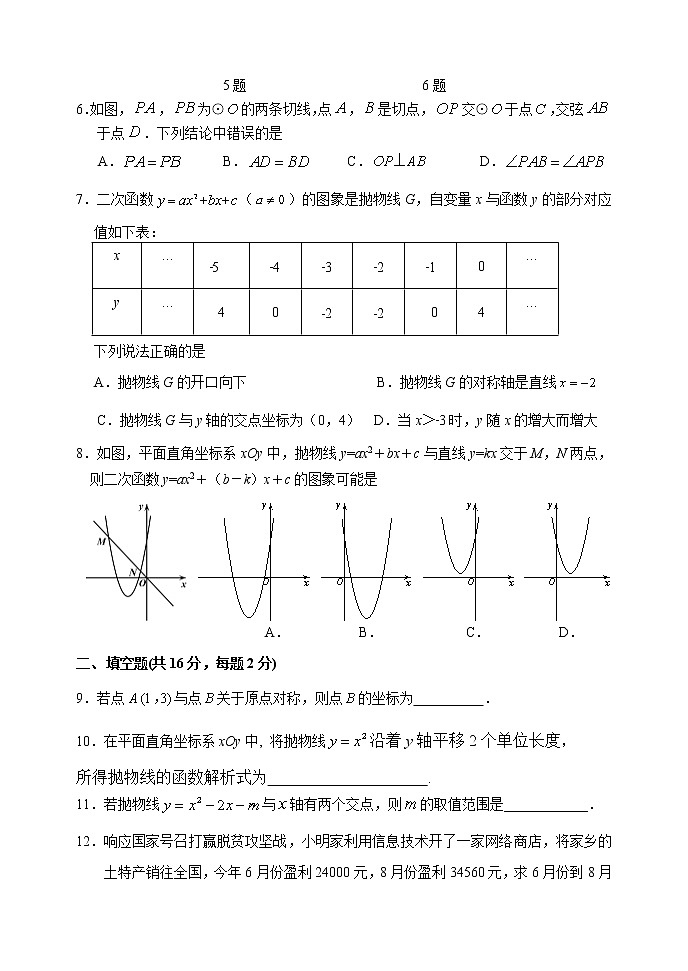
6．如图，，为⊙的两条切线，点，是切点，交⊙于点，交弦
于点．下列结论中错误的是
A．
B．
C．
D．
7．二次函数（）的图象是抛物线G，自变量x与函数y的部分对应值如下表：
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是
A．抛物线G的开口向下 B．抛物线G的对称轴是直线
C．抛物线G与y轴的交点坐标为（0，4） D．当x＞﹣3时，y随x的增大而增大
8．如图，平面直角坐标系xOy中，抛物线y=ax2＋bx＋c与直线y=kx交于M，N两点，则二次函数y=ax2＋（b－k）x＋c的图象可能是




A． B． C． D．
二、 填空题(共16分，每题2分)
9．若点与点关于原点对称，则点的坐标为 ．
10．在平面直角坐标系xOy中, 将抛物线沿着y轴平移2个单位长度，
所得抛物线的函数解析式为 .
11．若抛物线与轴有两个交点，则的取值范围是____________．
12．响应国家号召打赢脱贫攻坚战，小明家利用信息技术开了一家网络商店，将家乡的土特产销往全国，今年6月份盈利24000元，8月份盈利34560元，求6月份到8月份盈利的月平均增长率.设6月份到8月份盈利的月平均增长率为x，根据题意，可列方程为 .
13．如图所示的正方形网格中，A，B，C，D，P是网格线交点.若∠APB=α，则∠BPC的度数为 （用含α的式子表示）.
14．如图，正方形内接于⊙，点在上，则=________．




13题 14题 15题
15．如图，△ABC为等腰三角形，O是底边BC的中点，若腰AB与⊙O相切，则AC与⊙O的位置关系为 （填“相交”、“相切”或“相离”）．
16．如图1，在△ABC中，AB>AC， D是边BC上的动点. 设B，D两点之间的距离为x，A，D两点之间的距离为y， 表示 y与x的函数关系的图象如图2所示. 线段AC的长为 ，线段AB的长为 .





三、解答题（共68分）解答应写出文字说明、演算步骤或证明过程。
17．解方程： 18．解方程：


19．关于x的一元二次方程有两个不相等的实数根.
（1）求m的取值范围；
（2）若m为正整数，写出一个符合条件的m的值并求出此时方程的根.

20．如图1是博物馆展出的古代车轮实物，《周礼·考工记》记载：“……故兵车之轮六尺有六寸，田车之轮六尺有三寸……”据此， 我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．
图1 图2
如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为r cm．
作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理的依据是： ．
经测量，AB=90cm，CD=15cm，则AD= cm；
用含r的代数式表示OD，OD= cm．
在Rt△OAD中，由勾股定理可列出关于r的方程：
，解得r=75．
通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．

21．已知：如图，线段AB.
求作: 以AB为斜边的直角△ABC，使得一个内角等于30°．
作法：①作线段AB的垂直平分线交AB于点O；
②以点O为圆心，OA长为半径画圆；
③以点B为圆心，OB长为半径画弧与⊙O相交，记其中一个交点为C；
④分别连接AC，BC；
△ABC就是所求作的直角三角形.

(1)使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明.
证明：连接OC,
∵AB是⊙O的直径，
∴∠ACB= ° ( )(填推理的依据) .
∴△ABC是以AB为斜边的直角三角形.
∵OC=OB=BC,
∴△OBC是等边三角形.
∴∠COB=60°.
∴∠A= °.

22．已知二次函数.
（1）求二次函数图象的顶点坐标；
（2）在平面直角坐标系xOy中，画出二次函数的图象；
（3）当时，结合函数图象，直接写出y的取值范围．








23．已知抛物线．
（1）该抛物线的对称轴为 ；
（2）若该抛物线的顶点在x轴上，求抛物线的解析式；
（3）设点M（m，y1），N（2，y2）在该抛物线上，若y1＞y2，求m的取值范围．



24．如图，Rt△ABC中，∠ACB=90°，点D在BC边上，以CD为直径的⊙O与直线AB相切于点E，且E是AB中点，连接OA．
（1）求证：OA=OB；
（2）连接AD，若AD=，求⊙O的半径．



25．如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，过点D作AC的垂线，交AC的延长线于点E，连接AD．
（1）求证：是⊙O的切线；
（2）连接CD，若∠CDA=30°，AC=2，求CE的长．




26．在平面直角坐标系xOy中,抛物线（）过点(4,0)．
（1）用含a的代数式表示b；
（2）已知点A（0，a），将点A绕原点O顺时针旋转90°得到点B，再将点B向右
平移2个单位长度得到点C，求点C的坐标（用含a的代数式表示）；
（3）在（2）的条件下，若线段AC与抛物线有公共点，求a的取值范围.







27．在等腰直角△ABC中，AB= AC，BAC=90°，过点B作BC的垂线l.点P为直线AB上的一个动点（不与点A，B重合），将射线PC绕点P顺时针旋转90°交直线l于点D.
（1）如图1，点P在线段AB上，依题意补全图形；
①求证：∠BDP =∠PCB；
②用等式表示线段BC，BD，BP之间的数量关系，并证明.
（2）点P在线段AB的延长线上，直接写出线段BC，BD，BP之间的数量关系.

图1 备用图























28．在平面直角坐标系xOy中，⊙O的半径为2，A，B为⊙O外两点，AB=1.
给出如下定义：平移线段AB，使线段AB的一个端点落在⊙O上，其他部分不在⊙O外，
点A，B对应点分别为点A´，B´，线段A A´长度的最大值称为线段AB到⊙O的
“极大距离”，记为 d（AB，⊙O）.
（1）若点A（-4，0）.
①当点B为（-3，0），如图所示，平移线段AB，
在点P1（-2，0），P2（-1，0），P3（1，0），
P4（2，0）中，连接点A与点 的线段的
长度为d（AB，⊙O）；
②当点B为（-4，1），求线段AB到⊙O的
“极大距离”所对应的点A´的坐标；
（2）若点A（-4，4），d（AB，⊙O）的取值范围
是 .




















2021-2022学年度
九年级数学期中测试参考答案及评分标准 2021年11月

一、选择题(共16分，每题2分)
ADCDADCA
二、填空题(共16分，每题2分)
9. (-1,-3) 10. ,或 (各1分) 11．
12. 13. 14． 15．相切 16. (各1分)
三、解答题
17．解：方法一：

……………………………………………………3分

． ……………………………………………………5分
方法二：
.
, ……………………………………3分
． ……………………………………………………5分
方法三：
………………………………3分
或
． ……………………………………………………5分
18.x（x-3）=0……………………………………………………3分
……………………………………………………5分
19．解：（1）由题意，.
解得 . ………………………………………………2分
（2）m=1.
此时方程为
∴方程的根为. ………………………………………………5分
20. 垂直于弦的直径平分弦； ………………………………………………1分
45； ………………………………………………2分
； ………………………………………………3分
． ………………………………………………5分
21．解：（1）补全的图形如图所示.












┈┈┈┈┈┈┈┈┈┈┈┈┈ 3分
（2）90，直径所对的圆周角是直角，30.┈┈┈┈┈┈┈┈6分






22. 解：
（1） ∵，
∴该二次函数图象顶点坐标为(2，-1).
2分
（2） 如图：




4分
（3） -1≤y<3. 6分

23．解：（1）直线x＝－1. …… 1分
（2）∵抛物线顶点在x轴上，
∴顶点坐标为（－1，0）. …… 2分
解得.
∴抛物线解析式为或 . …… 4分
（3）∵抛物线的对称轴为直线x＝－1，
∴N（2，y2）关于直线x＝－1的对称点为N’（－4，y2）.
（ⅰ）当a＞0时，若y1＞y2，则m＜－4或m＞2；
（ⅱ）当a＜0时，若y1＞y2，则－4＜m＜2. …… 6分

24．（1）证明：在⊙O中，连接.
∵ 直线AB与⊙O相切于点E，
∴ OE⊥AB． …………1分
∵ E是AB中点，
∴ OA=OB． …………2分
（2）解：∵ OA=OB，
∴ ∠OAE=∠B．
∵∠ACB=90°，
∴AE，AC是⊙O的切线，
∴∠OAE=∠OAC．（切线长定理）
∴ ∠OAE=∠OAC=∠B．
∵ ∠OAE+∠OAC+∠B=90°，
∴ ∠OAC=30°． …………4分
设⊙O的半径为r，则CD=2r
在Rt△AOC中，AO=2OC=2r．
∴ ． …………5分
在Rt△ACD中，，，
∴ ，解得．
∴ ⊙O的半径为1． …………6分
25．（1） 证明：如图1，连接，…………1分
∵D是弧BC的中点，
∴∠BAD=∠CAD.
∵OA=，
∴∠BAD=∠ODA.
∴∠CAD=∠ODA.
∴OD//AE. …………2分
∵DE⊥AC，
∴DE⊥OD.
∴DE是⊙O的切线. …………3分
（2）解：如图2，连接OC，…………4分
∵∠CDA=30°，
∴∠AOC=2∠CDA=60°.
∴△AOC是等边三角形. …………5分
∴由（1）可得，四边形ACDO是菱形.
∴CD=AC=2，∠CDE=30°.
∴CE=1. …………6分
26解：
（1）∵抛物线y=ax2+bx过点(4，0)，
∴，
∴. 2分
（2）∵点A(0，a)绕原点O顺时针旋转90°得到点B，
∴点B的坐标为(a，0)， 3分
∵点B向右平移2个单位长度得到点C，
∴点C的坐标为(a+2，0). 4分
（3）（i）当a>0时，
抛物线y=ax2-4ax开口向上，与x轴交于两点(0，0)，(4，0).
若线段AC与抛物线有公共点（如图1），只需满足：
，解得：. 5分

图1
（ii）当a<0时，
抛物线y=ax2-4ax开口向下，与x轴交于两点(0，0)，(4，0).
若线段AC与抛物线有公共点（如图2），只需满足：
，解得：. 6分

图2
综上所述，a的取值范围为或.


27．解：（1）补全图形，如图. …………1分








①证明：如图①，设PD与BC的交点为E.
根据题意可知，∠CPD=90°.
∵BC⊥l，
∴∠DBC=90°.
∴∠BDP+∠BED=∠PCB+∠PEC= 90°.
∴∠BDP=∠PCB. …………2分
图①
②BC-BD=BP. …………3分

证明：如图②，过点P作PF⊥BP交BC于点F.
∵AB= AC，∠A=90°，
∴∠ABC=45°.
∴BP=PF，∠PFB=45°.
∴∠PBD=∠PFC=135°.
∴△BPD≌△FPC.………4分
图②
∴BD=FC.
∵BF=BP，
∴BC-BD=BP . …………5分
（3）BD-BC=BP. …………6分
28．（1）①. …………1分
②如图，⊥x轴于点M. ∴M为中点.
∵.…………2分
. …………3分
∴. …………4分
（2）…………6分