北京市平谷区2021—2022学年九年级上学期 数学期中试卷（word版 含答案）

这是一份北京市平谷区2021—2022学年九年级上学期 数学期中试卷（word版 含答案），共13页。试卷主要包含了已知，阅读下列材料等内容，欢迎下载使用。

2021—2022学年度第一学期
初三年级数学学科期中测试
班级________ 姓名________ 学号________
第Ⅰ卷（选择题 共16分）
一、 选择题：（每小题2分，共16分）
1．抛物线的开口方向和顶点坐标分别是（ ）
A．向上， B．向下，
C．向下， D．向上，
2.在下列图案中，既是轴对称图形，又是中心对称图形的是( )




A
B
C
D
3．若关于x的一元二次方程有一个根为0，则a的值为( )
A. B. C. 2 D.
4．如图，△ABC内接于⊙O，连结OA，OB，∠ABO=40°，
则∠C的度数是（ ）.
A. 100° B. 80° C.50° D.40°
5.关于x的一元二次方程有实数根，则的取值范围是（ ）.
A． B． C．且 D．且
6．如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段
BC的延长线上，则的大小为（ ）.
A．30° B．40°
C．50° D．60°

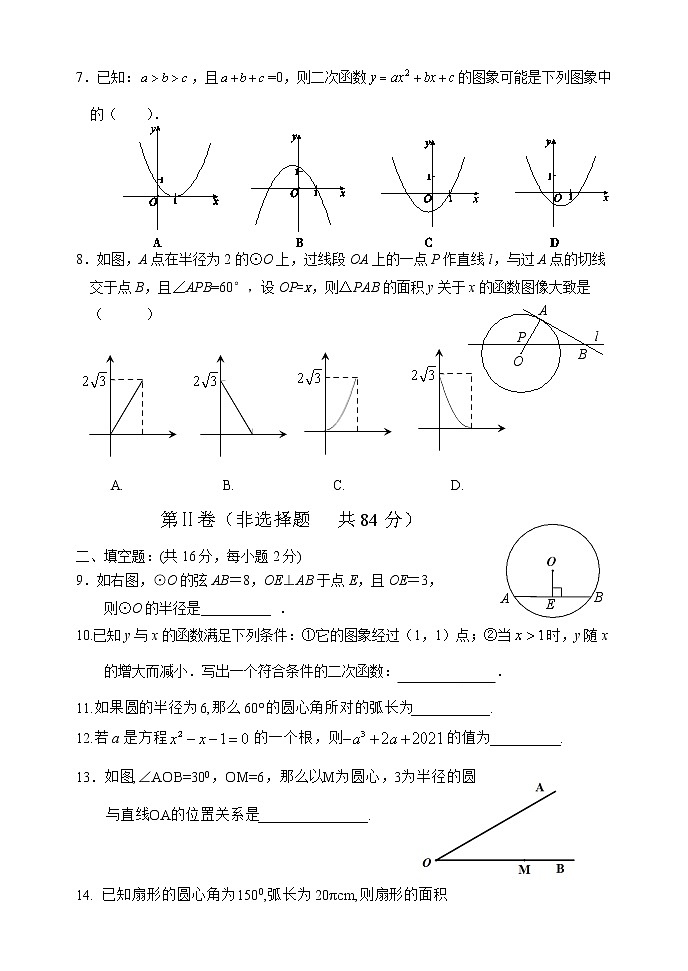
7．已知：，且=0，则二次函数的图象可能是下列图象中的（ ）．





P
O
B
A
l
8．如图，A点在半径为2的⊙O上，过线段OA上的一点P作直线l，与过A点的切线交于点B，且∠APB=60°，设OP=x，则△PAB的面积y关于x的函数图像大致是（ ）





















A. B. C. D.
A
B
E
第Ⅱ卷（非选择题 共84分）
二、填空题：(共16分，每小题2分)
9．如右图，⊙O的弦AB＝8，OE⊥AB于点E，且OE＝3，
则⊙O的半径是__________ ．
10.已知y与x的函数满足下列条件：①它的图象经过（1，1）点；②当时，y随x的增大而减小．写出一个符合条件的二次函数： ____ ．
11.如果圆的半径为6,那么60°的圆心角所对的弧长为__________.
12.若a是方程的一个根，则的值为_________.
13．如图,∠AOB=300，OM=6，那么以M为圆心，3为半径的圆
与直线OA的位置关系是______________.

14. 已知扇形的圆心角为1500,弧长为20πcm,则扇形的面积
_______cm2.
15．如图，正方形ABCD的边长为1，AC，BD是对角线．将
△DCB绕着点D顺时针旋转45º得到△DGH，HG交AB
于点E，连接DE交AC于点F，连接FG.则下列结论：
①四边形AEGF是菱形；②△AED≌△GED；
③∠DFG=112.5º；④BC+FG=1.5，其中正确的结论是 .
16．下面是“作一个30°角”的尺规作图过程．
已知：平面内一点A．
求作：∠A，使得∠A30°．
作法：如图，
（1）作射线AB；
（2）在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C；
（3）以C为圆心，OC为半径作弧，与⊙O交于点D，作射线AD．
∠DAB即为所求的角．

请回答：该尺规作图的依据是_________________________________________________________________________________________________________________________________________________．
三、解答题（本题共68分，第17题每小题4分，第18题至第20题每小题5分，第21题至第24题每小题6分，第25题至第27题每小题7分）
17．解下列方程:（1）； （2）


18．二次函数图象上部分点的横坐标x，纵坐标y的对应值如下表：
x
…







…
y
…







…
（1）求这个二次函数的表达式；
（2）在图中画出这个二次函数的图象．
（3）当函数值时，对应的x的取值范
围是_____________.
（4）当自变量x的取值范围是时，
那么对应函数值y的取值范围是________.




19.如图，四边形ABCD是⊙O的内接四边形，对角线
AC是⊙O的直径，AB=2，∠ADB＝45°.求⊙O半径的长.



20．已知：关于x的一元二次方程x2 - 2x + m -1= 0有两个不相等的实数根．
（1）求m的取值范围；
（2）如果m为非负整数，且该方程的根都是整数，求m的值．

21．如图，AB是⊙O的直径，C，D为⊙O上两点，CF⊥AB
于点F，CE⊥AD交AD的延长线于点E，且CE=CF．
（1）求证：CE是⊙O的切线；
（2）连接CD，CB．若AD=CD=3，求四边形ABCD
面积．



22．阅读下列材料：
问题：如图⑴，已知正方形ABCD中，E、F分别是BC、CD边上的点，且
∠EAF ＝45°． 判断线段BE、EF、FD之间的数量关系，并说明理由．

小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△DAF绕点A顺时针旋转90°，得到△BAH，然后通过证明三角形全等可得出结论．





图（1） 图（2） 图（3）
请你参考小明同学的思路，解决下列问题：
⑴ 图⑴中线段BE、EF、FD之间的数量关系是 ；
⑵ 如图⑵，已知正方形ABCD边长为5，E、F分别是BC、CD边上的点，且
∠EAF＝45°，AG⊥EF于点G，则AG的长为 ，△EFC的周长为 ；
⑶ 如图⑶，已知△AEF中，∠EAF＝45°，AG⊥EF于点G，且EG＝2，GF＝3，求△AEF的面积.写出解答过程

23．小明爸爸经营的水果店出售一种优质热带水果，正在上初三的小明经过调查和计算，发现这种水果每月的销售量y(千克)与销售单价x（元）之间存在着一次函数关系：y=-10x+500．下面是他们的一次对话：
小明：“您要是告诉我咱家这种水果的进价是多少？我就能帮你预测好多信息呢！”
爸爸：“咱家这种水果的进价是每千克20元”
聪明的你，也来解答一下小明想要解决的三个问题：
（1）若每月获得利润w(元）是销售单价x（元）的函数，求这个函数的解析式．
（2）当销售单价为多少元时，每月可获得最大利润？
（3）如果想要每月从这种水果的销售中获利2000元，那么销售单价应该定为多少元？
24．如图，在△ABC中，，°，点D是线段BC上的动点，将线段AD绕点A顺时针旋转50°至，连接．已知AB2cm，设BD为x cm，B为y cm．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究，下面是小明的探究过程，请补充完整．（说明：解答中所填数值均保留一位小数）
（1）通过取点、画图、测量，得到了与的几组值，如下表：


0.5
0.7
1.0
1.5
2.0
2.3

1.7
1.3
1.1

0.7
0.9
1.1

（2）建立平面直角坐标系，描出以补
全后的表中各对对应值为坐标的点，
画出该函数的图象．





（3）结合画出的函数图象，解决问题：
线段的长度的最小值约为__________；若，则的长度x的取值范围是______________________．
25. 已知抛物线l1与l2形状相同，开口方向不同，其中抛物线l1：交x轴于A，B两点（点A在点B的左侧），且AB＝6；抛物线l2与l1交于点A和点
C（5，n）.
（1）求抛物线l1，l2的表达式；
（2）当抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大时，求x的取值范围；
（3）直线MN∥y轴，交x轴，l1，l2分别相交于点P（m，0），M，N，当1≤m≤7时，求线段MN的最大值.


26．如图，△ABC为等边三角形，点P是线段AC上一动点(点P不与A,C重合)，连接BP，过点A作直线BP的垂线段，垂足为点D，将线段AD绕点A逆时针旋转得到线段AE,连接DE,CE．
（1）求证：BD=CE；
（2）延长ED交BC于点F，求证：F为BC的中点；
（3）若△ABC的边长为1，直接写出EF的最大值.

27. 在平面直角坐标系xOy中，点P的横坐标为x，纵坐标为2x，满足这样条件的点称为“关系点”.
(1)在点A(1,2)、B(2,1)、M(，1)、N(1，)中，是“关系点”的 ；
(2)⊙O的半径为1，若在⊙O上存在“关系点”P，求点P坐标；
(3)点C的坐标为(3，0)，若在⊙C上有且只有一个“关系点”P，且“关系点”P的横坐标满足.请直接写出⊙C的半径r的取值范围．















2021—2022学年度第一学期
初三年级数学期中测试答案部分
一、 选择题：每题_2_分，共_16_分
题号
1
2
3
4
5
6
7
8
答案
B
A
D
C
C
B
C
D

二、 填空题：每小题2分，共16分
（9）5 ； （10）不唯一，例如：； （11）； （12）2020；
（13）相切； （14）； （15）①②③
（16）三条边相等的三角形是等边三角形，等边三角形的三个内角都是60°，一条弧所对的圆周角是它所对圆心角的一半；
或：直径所对的圆周角为直角，三条边相等的三角形是等边三角形，等边三角形的三个内角都是60°，直角三角形两个锐角互余；
三、 解答题：（本题共68分，第17题每小题4分，第18题至第20题每小题5分，第21题至第24题每小题6分，第25题至第27题每小题7分）
17．（1）； （2）；
18．（1）解析式：；………….2分
（2）略………………..3分
（3）……………….4分
（4）…………….5分
19．证明略，半径长为…………………5分
20．（1）……………2分
（2）………………….3分
21．（1）证明：连接OC，AC．
∵CF⊥AB，CE⊥AD，且CE=CF．
∴∠CAE=∠CAB. …………………………………………………… 1分
∵OC= OA，
∴∠CAB=∠OCA.
∴∠CAE=∠OCA.
∴OC∥AE．
∴∠OCE+∠AEC=180°，
∵∠AEC=90°，
∴∠OCE=90°即OC⊥CE，
∵OC是⊙O的半径，点C为半径外端，
∴CE是⊙O的切线．…………………………………………………3分
（2）求解思路如下：
①由AD=CD=3，得到∠DAC=∠DCA，于是∠DCA=∠CAB，可知DC∥AB；
⌒ ⌒

②由OC∥AE，OC=OA，可知四边形AOCD是菱形；……………4分
③由∠CAE=∠CAB，得到CD=CB，DC=BC=3，可知△OBC为等边三角形；
④由等边△OBC可求高CF的长，进而可求四边形ABCD面积. ……6分
22．（1）…………………2分
（2）5，10………………..4分
（3）15…………….6分
23．（1）………………..2分
(2) 35……………………………..4分
（3）30和40……………………….6分

24．（1）0.9. ………………1分
（2）如右图所示.………………3分
（3）0.7，………………4分
.………………6分

25. 解：（1）由题意可知，抛物线l1的对称轴为直线. …………1分
∵抛物线l1交x轴于A，B两点（点A在点B左侧），且AB＝6，
∴A（1，0），B（7，0）.
把A（1，0）代入，解得.
∴抛物线l1的表达式为. ………………………………………2分
把C（5，n）代入，解得. ∴C（5，4）.
∵抛物线l1与l2形状相同，开口方向不同，.
∴设抛物线l2的表达式为.
把A（1，0），C（5，4）代入，得，解得.
∴抛物线l2的表达式为. ………………………………………………3分
（2）2≤x≤4；…………………………………………………………………4分

（3）∵直线MN∥y轴，交x轴，l1，l2于点P（m，0），M，N，
∴M（m，），N（m，）. ………5分

① 如图1，当1≤m≤5时，

∴当m＝3时，MN的最大值为4；

……………6分图1

② 如图2，当5﹤m≤7时，

4﹤m≤7在对称轴m＝3右侧，
MN随m的增大而增大.
∴当m＝7时，MN的最大值是12.
……………7分
综上所述，线段MN的最大值是12.
26．∵线段AD绕点A逆时针旋转得到线段AE,
∴△ADE是等边三角形.
在等边△ABC和等边△ADE中
AB＝AC
AD＝AE
∠BAC＝∠DAE＝60°
∴∠BAD＝∠CAE……………………………………………………1分
在△BAD和△CAE中

∴△BAD≌△CAE（SAS）……………………………2分
∴BD=CE ……………………………………3分

（2）如图，过点C作CG∥BP交DF的延长线于点G
∴∠G＝∠BDF
∵∠ADE＝60°，∠ADB＝90°
∴∠BDF＝30°
∴∠G＝30°……………………………………………………4分
由（1）可知，BD＝CE，∠CEA＝∠BDA
∵AD⊥BP
∴∠BDA＝90°
∴∠CEA＝90°
∵∠AED＝60°，
∴∠CED＝30°=∠G，
∴CE＝CG
∴BD＝CG ……………………………………………………5分
在△BDF和△CGF中

∴△BDF≌△CGF（AAS）
∴BF＝FC
即F为BC的中点．……………………………………………………6分
（3）1……………………………………………………7分

27. 解：(1)A、M. …………………………………………………………2分
(2)过点P作PG⊥x轴于点G……………………………………………………3分
设P（x，2x）
∵OG2+PG2=OP2 ……………………………………………………………………4分
∴x2+4x2=1
∴5x2=1
∴x2=∴x=
∴P(，)或P(，)………………5分
(3)r=或 ……………………………………7分