人教版2021年七年级上册期末第1-4章综合性复习训练卷 含答案

这是一份人教版2021年七年级上册期末第1-4章综合性复习训练卷 含答案，共13页。试卷主要包含了下列说法中错误的是，下列运算正确的是，下列去括号中，正确的是等内容，欢迎下载使用。
人教版2021年七年级上册期末第1-4章综合性复习训练卷
一．选择题
1．如果一个物体向右移动2米记作移动+2米，那么这个物体又移动了﹣2米的意思是（　　）
A．物体又向右移动了2米 B．物体又向右移动了4米
C．物体又向左移动了2米 D．物体又向左移动了4米
2．在数0，2，﹣3，﹣1.2中，属于负整数的是（　　）
A．0 B．2 C．﹣3 D．﹣1.2
3．中国设计并制造的“神威•太湖之光”是世界上首台峰值运算速度超过每秒十亿亿次的超级计算机，其核心是完全由中国自主研发的40960块高性能处理器．40960用科学记数法表示为（　　）
A．0.4096×105 B．4.096×104 C．40.96×103 D．4096×10
4．下列说法中错误的是（　　）
A．线段AB和射线AB都是直线的一部分
B．直线AB和直线BA是同一条直线
C．射线AB和射线BA是同一条射线
D．线段AB和线段BA是同一条线段
5．下列运算正确的是（　　）
A．4a﹣3a＝1 B．a2+a2＝a4
C．3a2+2a2＝5a2 D．4a+3b＝7ab
6．下列去括号中，正确的是（　　）
A．a2﹣（2a﹣1）＝a2﹣2a﹣1
B．a2+（﹣2a﹣3）＝a2﹣2a+3
C．3a﹣[5b﹣（2c﹣1）]＝3a﹣5b+2c﹣1
D．﹣（a+b）+（c﹣d）＝﹣a﹣b﹣c+d
7．多项式1+2xy﹣3xy2的次数及最高次项的系数分别是（　　）
A．3，﹣3 B．2，﹣3 C．5，﹣3 D．2，3
8．某车间30名工人生产螺母和螺钉，每人每天平均生产螺钉1500个或螺母4500个，一个螺钉要配两个螺母，已知每天生产的产品刚好配套，若设安排x名工人生产螺钉，则可列方程为（　　）
A．4500（30﹣x）＝2×1500x B．2×4500（30﹣x）＝1500x
C．4500 x＝2×1500（30﹣x） D．4500 x+2×1500x＝30
9．在平面内，∠AOB＝60°，∠COB＝30°，则∠AOC等于（　　）
A．30° B．30°或60° C．30°或90° D．90°
10．如图，D、E顺次为线段AB上的两点，AB＝19，BE﹣DE＝7，C为AD的中点，则AE﹣AC的值为（　　）

A．5 B．6 C．7 D．8
二．填空题
11．计算：18°36′＝　 　°．
12．当x＝﹣1时，多项式2﹣3x+1的值为　 　．
13．数轴上表示数﹣5和表示﹣14的两点之间的距离是　 　．
14．若|a|＝2，|b|＝3，且a＞b，则a﹣b＝　 　．
15．若单项式5am+1b和25a4bn﹣1是同类项，则mn的值为　 　．
16．商场将一件商品在进价的基础上加价80%标价，再九折出售，结果获利62元，则这件商品的进价为　 　元．
三．解答题
17．计算：÷（﹣2÷3）2×（﹣2）3﹣2×|（﹣1）7×+1|





18．先化简，再求值：3a2+（4a2﹣2a﹣1）﹣2（3a2﹣a+1），其中a＝．





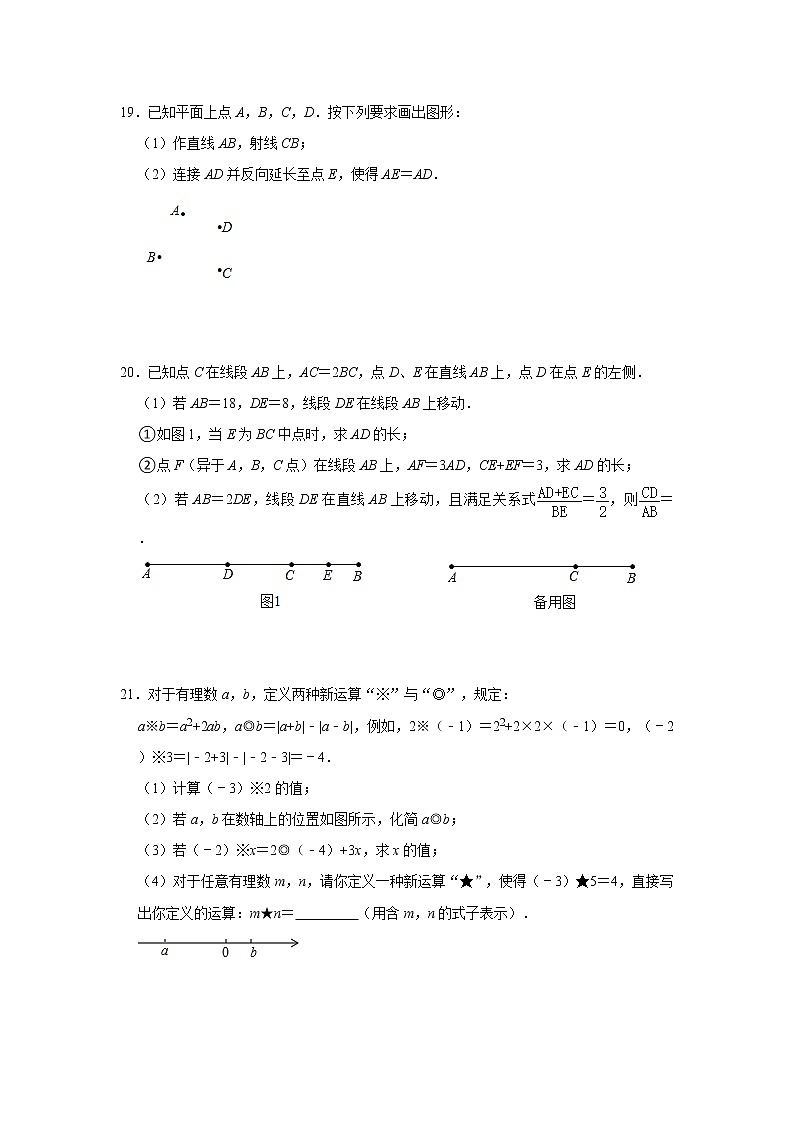
19．已知平面上点A，B，C，D．按下列要求画出图形：
（1）作直线AB，射线CB；
（2）连接AD并反向延长至点E，使得AE＝AD．



20．已知点C在线段AB上，AC＝2BC，点D、E在直线AB上，点D在点E的左侧．
（1）若AB＝18，DE＝8，线段DE在线段AB上移动．
①如图1，当E为BC中点时，求AD的长；
②点F（异于A，B，C点）在线段AB上，AF＝3AD，CE+EF＝3，求AD的长；
（2）若AB＝2DE，线段DE在直线AB上移动，且满足关系式＝，则＝　 　．



21．对于有理数a，b，定义两种新运算“※”与“◎”，规定：
a※b＝a2+2ab，a◎b＝|a+b|﹣|a﹣b|，例如，2※（﹣1）＝22+2×2×（﹣1）＝0，（﹣2）※3＝|﹣2+3|﹣|﹣2﹣3|＝﹣4．
（1）计算（﹣3）※2的值；
（2）若a，b在数轴上的位置如图所示，化简a◎b；
（3）若（﹣2）※x＝2◎（﹣4）+3x，求x的值；
（4）对于任意有理数m，n，请你定义一种新运算“★”，使得（﹣3）★5＝4，直接写出你定义的运算：m★n＝　 　（用含m，n的式子表示）．



22．如图，已知锐角∠AOB，射线OC不与OA，OB重合，OM，ON分别平分∠AOC，∠BOC．
（1）当OC在∠AOB的内部
①若∠BOC＝50°，∠AOC＝20°，求∠MON的大小；
②若∠MON＝30°，求∠AOB的大小；
（2）当射线OC在∠AOB外部，且∠AOB＝80°，请直接写出∠MON的大小．




23．如图1，点A，B，C，D为直线l上从左到右顺次的4个点．
（1）①直线l上以A，B，C，D为端点的线段共有　 　条；
②若AC＝5cm，BD＝6cm，BC＝1cm，点P为直线l上一点，则PA+PD的最小值为　 　cm；
（2）若点A在直线l上向左运动，线段BD在直线l上向右运动，M，N分别为AC，BD的中点（如图2），请指出在此过程中线段AD，BC，MN有何数量关系并说明理由；
（3）若C是AD的一个三等分点，DC＞AC，且AD＝9cm，E，F两点同时从C，D出发，分别以2cm/s，1cm/s的速度沿直线l向左运动，Q为EF的中点，设运动时间为t，当AQ+AE+AF＝AD时，请直接写出t的值．



参考答案
一．选择题
1．解：如果一个物体向右移动2米记作移动+2米，那么这个物体又移动了﹣2米的意思是：物体又向左移动了2米．
故选：C．
2．解：在这些数0，2，﹣3，﹣1.2中，属于负数的有﹣3，﹣1.2，
则属于负整数的是﹣3；
故选：C．
3．解：将40960这个数用科学记数法表示为4.096×104．
故选：B．
4．解：A、线段AB和射线AB都是直线的一部分，正确，不合题意；
B、直线AB和直线BA是同一条直线，正确，不符合题意；
C、射线AB和射线BA不是同一条射线，错误，符合题意；
D、线段AB和线段BA是同一条线段，正确，不合题意；
故选：C．
5．解：A、4a﹣3a＝a，故此选项错误；
B、a2+a2＝2a2，故此选项错误；
C、3a2+2a2＝5a2，故此选项正确；
D、4a+3b，无法合并，故此选项错误．
故选：C．
6．解：A，a2﹣（2a﹣1）＝a2﹣2a+1，故此选项错误；
B，a2+（﹣2a﹣3）＝a2﹣2a﹣3，故此选项错误；
C，3a﹣[5b﹣（2c﹣1）]＝3a﹣5b+2c﹣1，故此选项正确；
D，﹣（a+b）+（c﹣d）＝﹣a﹣b+c﹣d，故此选项错误；
故选：C．
7．解：多项式1+2xy﹣3xy2的次数是3，
最高次项是﹣3xy2，系数是﹣3；
故选：A．
8．解：设安排x名工人生产螺钉，则安排（30﹣x）名工人生产螺母，
依题意，得：2×1500x＝4500（30﹣x）．
故选：A．
9．解：∠COB如果在∠AOB内部，则∠AOC＝∠AOB﹣∠COB＝30°；
∠COB如果在∠AOB的外部，则∠AOC＝∠AOB+∠COB＝90°．
故选：C．
10．解：∵AB＝19，设AE＝m，
∴BE＝AB﹣AE＝19﹣m，
∵BE﹣DE＝7，
∴19﹣m﹣DE＝7，
∴DE＝12﹣m，
∴AD＝AB﹣BE﹣DE
＝19﹣（19﹣m）﹣（12﹣m）
＝19﹣19+m﹣12+m
＝2m﹣12，
∵C为AD中点，
∴AC＝AD＝×（2m﹣12）＝m﹣6．
∴AE﹣AC＝6，
故选：B．
二．填空题
11．解：18°36′＝18°+（36÷60）°＝18.6°，
故答案为：18.6．
12．解：∵x＝﹣1，
∴2﹣3x+1
＝2﹣3×（﹣1）+1
＝6
故答案为：6．
13．解：|﹣5﹣（﹣14）|＝9．
14．解：∵|a|＝2，|b|＝3，且a＞b，
∴a＝±2，b＝﹣3；
当a＝2，b＝﹣3时，a﹣b＝5，
当a＝﹣2，b＝﹣3时，a﹣b|＝1．
故答案为：5或1．
15．解：∵单项式5am+1b和25a4bn﹣1是同类项，
∴m+1＝4，n﹣1＝1，
解得：m＝3，n＝2，
则mn＝32＝9．
故答案为：9．
16．解：设这件商品的进价为x元，
由题意得：90%（1+80%）x﹣x＝62
解得：x＝100
∴这件商品的进价为100元，
故答案为：100．
三．解答题
17．解：÷（﹣2÷3）2×（﹣2）3﹣2×|（﹣1）7×+1|
＝÷（﹣）2×（﹣8）﹣2×|1×+1|
＝÷×（﹣8）﹣2×|+1|
＝﹣2×
＝﹣
＝﹣1．
18．解：原式＝3a2+4a2﹣2a﹣1﹣6a2+2a﹣2
＝a2﹣3
当a＝时，
原式＝﹣3
＝﹣
19．解：（1）如图所示：
（2）如图所示．

20．解：（1）AC＝2BC，AB＝18，DE＝8，
∴BC＝6，AC＝12，
①如图，

∵E为BC中点，
∴CE＝3，
∴CD＝5，
∴AD＝AB﹣DB＝18﹣11＝7；
②如图，

Ⅰ、当点E在点F的左侧，
∵CE+EF＝3，BC＝6，
∴点F是BC的中点，
∴CF＝BF＝3，
∴AF＝AB﹣BF＝18﹣3＝15，
∴AD＝AF＝5；
Ⅱ、当点E在点F的右侧，

∵AC＝12，CE+EF＝CF＝3，
∴AF＝AC﹣CF＝9，
∴AF＝3AD＝9，
∴AD＝3．
综上所述：AD的长为3或5；
（2）∵AC＝2BC，AB＝2DE，满足关系式＝，
Ⅰ、当点E在点C右侧时，如图，

设CE＝x，DC＝y，
则DE＝x+y，
∴AB＝2（x+y）
AC＝AB＝（x+y）
∴AD＝AC﹣DC＝x+y
BC＝AB＝（x+y）
∴BE＝BC﹣CE＝y﹣x
∴AD+EC＝x+y
∵2（AD+EC）＝3BE
∴2（x+y）＝3（y﹣x）
解得，17x＝4y，
∴＝＝＝．
Ⅱ、当点E在点A左侧时，如图，

设CE＝x，DC＝y，
则DE＝y﹣x，
∴AB＝2（y﹣x）
AC＝AB＝（y﹣x）
∴AD＝DC﹣AC＝x﹣y
BC＝AB＝（y﹣x）
∴BE＝BC+CE＝y+x
∴AD+EC＝x﹣y
∵2（AD+EC）＝3BE
∴2（x﹣y）＝3（y+x）
解得，11x＝8y，
∴＝＝．
点D在C点右侧，及点D在B点右侧，
无解，不符合题意；
当DE在线段AC内部时，如图，

设CE＝x，DC＝y，
则DE＝y﹣x，
∴AB＝2（y﹣x），
AC＝AB＝（y﹣x），
∴AD＝AC﹣DC＝y﹣x，
BC＝AB＝（y﹣x），
∴BE＝BC+CE＝y+x，
∴AD+EC＝﹣x+y，
∵2（AD+EC）＝3BE
∴2（﹣x+y）＝3（y+x），
解得，﹣5x＝4y（不符合题意，舍去），
∴＝＝＜，不符合题意，舍去．
故答案为或．
21．解：（1）根据题中的新定义得：原式＝（﹣3）2+2×（﹣3）×2＝9﹣12＝﹣3；
（2）由a，b在数轴上位置，可得a+b＜0，a﹣b＜0，
则a◎b＝|a+b|﹣|a﹣b|＝﹣a﹣b+a﹣b＝﹣2b；
（3）∵（﹣2）※x＝2◎（﹣4）+3x，
∴22﹣4x＝2﹣6+3x，
解得：x＝；
（4）∵（﹣3）★5＝4，
∴m★n＝m2﹣n，
故答案为：m2﹣n．
22．解：（1）当OC在∠AOB的内部
①∵∠BOC＝50°，∠AOC＝20°，
OM，ON分别平分∠AOC，∠BOC
∴∠MOC＝∠AOC＝10°，∠NOC＝∠BOC＝25°
∴∠MON＝∠MOC+∠NOC＝10°+25°＝35°
答：∠MON的大小为35°；
②∵OM，ON分别平分∠AOC，∠BOC
∴∠AOC＝2∠MOC，∠BOC＝2∠NOC
∴∠AOB＝∠AOC+∠BOC
＝2（∠MOC+∠NOC）
＝2∠MON
∵∠MON＝30°，
∴∠AOB＝60°
答：∠AOB的大小为60°．
（2）当射线OC在∠AOB外部，且∠AOB＝80°，
分两种情况：
①如图1所示，

OM，ON分别平分∠AOC，∠BOC
∴∠MOC＝∠AOC，∠NOC＝∠BOC
∴∠MON＝∠NOC﹣∠MOC
＝∠BOC﹣∠AOC
＝（∠BOC﹣∠AOC）
＝AOB
＝40°；
②如图2所示，

OM，ON分别平分∠AOC，∠BOC
∴∠MOC＝∠AOC，∠NOC＝∠BOC
∴∠MON＝∠NOC+∠MOC
＝∠BOC+∠AOC
＝（∠BOC+∠AOC）
＝（360°﹣∠AOB）
＝280°
＝140°；
答：∠MON的大小为40°或140°
23．解：（1）①线段有：AB，AC，AD，BC，BD，CD，共6条；
故答案为：6；
②∵AC＝5cm，BD＝6cm，BC＝1cm，
∴AD＝AC+BD﹣BC＝5+6﹣1＝10
∵当点P位于线段AD上时，PA+PD的值最小
∴PA+PD的最小值为10cm
故答案为：10；

（2）当点B在点C左边时，AD﹣BC＝2MN；当点B在点C右边时，AD+BC＝2MN．
理由：当点B在点C左边，如图

AD+BC＝AC+BD＝2MC+2BN＝2（MC+BN）＝2（MN+BC），
AD﹣BC＝2MN，
当点B不在点C左边时，如图，

AD﹣BC＝AC+BD＝2MC+2BN＝2（MC+BN）＝2（MN﹣BC），
AD+BC＝2MN，

（3）∵C是AD的一个三等分点，DC＞AC，且AD＝9cm，
∴AC＝3cm，
设A点为数轴AD上的原点，向右为正方向，由题意得，
E点表示的数为：3﹣2t，F表示的数为：9﹣t，
∵Q是EF的中点，
∴Q点表示的数为：（3﹣2t+9﹣t）＝6﹣t，
∵AQ+AE+AF＝AD，
∴|6﹣t|+|3﹣2t|+|9﹣t|＝，
化简得，|12﹣3t|+|6﹣4t|+|18﹣2t|＝27，
当0＜t≤1.5时，有12﹣3t+6﹣4t+18﹣2t＝27，得t＝1；
当1.5＜t≤4时，有12﹣3t+4t﹣6+18﹣2t＝27，得t＝﹣3＜0（舍去）；
当4＜t≤9时，有﹣12+3t﹣6+4t+18﹣2t＝27，得t＝5.4；
当t≥9时，有﹣12+3t﹣6+4t﹣18+2t＝27，得t＝7＜9（舍去）；
故t＝1或5.4．