初中数学人教版七年级下册5.3.1 平行线的性质公开课课件ppt

这是一份初中数学人教版七年级下册5.3.1 平行线的性质公开课课件ppt，共23页。PPT课件主要包含了复习回顾，两直线平行，同位角相等，内错角相等，同旁内角互补，请注意，角的关系，说明直线平行，角相等或互补，说明角相等或互补等内容，欢迎下载使用。

1.对比分析平行线的判定和性质的区别。2.理解并掌握平行线中常见辅助线作法。
1.灵活运用平行线的判定和性质解决问题。
1.学会用几何语言准确描述辅助线？积累基本模型，用模型解决问题。
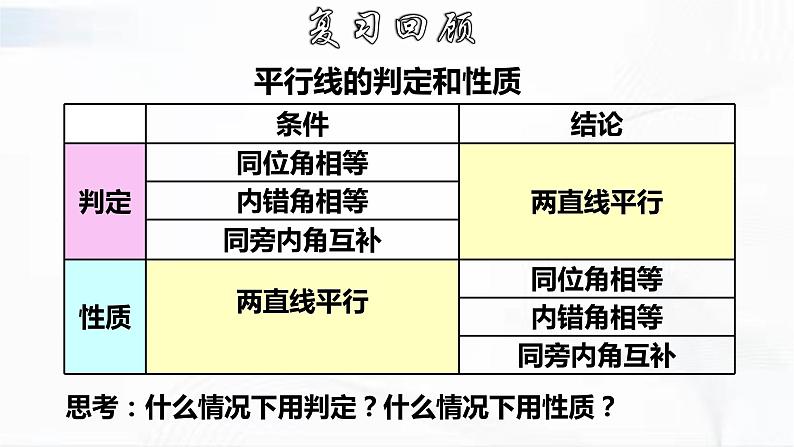
思考：什么情况下用判定？什么情况下用性质？
1.由_________得到___________的结论是平行线的判定;
2.由____________得到______________的结论是平行线的性质。
1．如图，AB，CD被EF所截，AB//CD。按要求填空：
若∠1＝120°，则∠2＝_____°（　　　　　　　　　　）；∠3＝_____－ ∠1＝_____°（　　　　　　　　　　　）
两直线平行，内错角相等。
两直线平行，同旁内角互补。
2．如图，已知AB//CD，AD//BC．填空：　　 （1）∵ AB//CD （已知），　　　　∴ ∠1＝ ∠____（ 　　　 ）；　 （2） ∵ AD//BC （已知） ∴ ∠2＝ ∠______（　 　　 　　　　）．
证明：∵AB∥ CD(已知)∴∠B=∠C( )∵CB∥ DE(已知)∴∠C+∠D=180°( )∴∠B+∠D=180°( )
如图：已知：AB∥ CD，CB∥ DE,试说明∠B+∠D=180°。
两直线平行，同旁内角互补
两直线平行，内错角相等
（同位角相等，两直线平行）
（两直线平行，同位角相等）
（内错角相等，两直线平行）
例1：已知：如图∠1＝∠2， ∠A＝∠C,试说明：AE∥ BC。
例2：如图：BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H。∠GFH+∠BHC=180°，求证：∠1=∠2。
解：∵∠BHC=∠FHD，∠GFH+∠BHC=180°（已知）∴∠GFH+∠FHD=180°（等量代换)∴FG∥ BD（同旁内角互补，两直线平行）∴∠1=∠ABD（两直线平行，同位角相等）∵BD平分∠ABC（已知）∴∠2=∠ABD（角平分线的定义）∴∠1=∠2（等量代换)
【长春模拟】如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F。（1）CD与EF平行吗？为什么？（2）如果∠1=∠2，且∠3=65°，那么∠ACB=____度。
解：（1）∵CD⊥AB，EF⊥AB（已知）∴CD∥ EF（平面内垂直于同一条直线的两条直线互相平行）（2）∵EF∥ DC∴∠2=∠BCD（两直线平行同位角相等）∵∠1=∠2（已知）∴∠1=∠BCD（等量代换）∴DG∥ BC（内错角相等，两直线平行）∴∠ACB=∠3=65°（两直线平行同位角相等）
如图， AB∥EF， CD∥EF ，试说明∠B、∠D、∠BED的大小关系。
解：∠B+∠D=∠BED。理由：∵AB∥ CD， EF∥ AB （已知）∴AB∥ CD∥ EF（平面内两条直线都与同一条直线平行，这两条直线互相平行）∴∠B=∠BEF，∠D=∠DEF（两直线平行，内错角相等）∵∠BEF+ ∠DEF =∠BED∴ ∠B+∠D=∠BED
如图，AB∥CD，试说明∠B、∠D 、∠BED之间的大小关系。
辅助线：为帮助解题而添加的线。
解：∠B+∠D=∠BED。理由：过点E作EF∥ AB∵AB∥ CD， EF∥ AB （已知）∴AB∥ CD∥ EF（平面内两条直线都与同一条直线平行，这两条直线互相平行）∴∠B=∠BEF，∠D=∠DEF（两直线平行，内错角相等）∵∠BEF+ ∠DEF =∠BED∴ ∠B+∠D=∠BED
1.如图，AB∥CD，试说明∠B、∠D 、∠BED之间的大小关系。
需要辅助线吗？怎样添加？
类型一：含一个拐点的平行线问题
解：∠B+∠D+∠BED=360°。理由：过点E作EF∥ AB∵AB∥ CD， EF∥ AB （已知）∴AB∥ CD∥ EF（平面内两条直线都与同一条直线平行，这两条直线互相平行）∴∠B+∠BEF=180°，∠D+∠DEF=180°（两直线平行，同旁内角互补）∵∠BEF+ ∠DEF =∠BED∴ ∠B+∠D+∠BED=360°
2.如图，AB∥ CD，试说明∠B、∠D 、∠BED之间的大小关系。
解：∠D+∠BED=∠B。理由：过点E作EF∥ AB∵AB∥ CD， EF∥ AB （已知）∴AB∥ CD∥ EF（平面内两条直线都与同一条直线平行，这两条直线互相平行）∴∠B=∠BEF，∠D=∠DEF（两直线平行，内错角相等）∵∠DEF+ ∠BED =∠BEF∴ ∠D+∠BED=∠B
3.如图，AB∥ CD，试说明∠B、∠D 、∠BED之间的大小关系。
解：∠B+∠BED=∠D。理由：过点E作EF∥ AB∵AB∥ CD， EF∥ AB （已知）∴AB∥ CD∥ EF（平面内两条直线都与同一条直线平行，这两条直线互相平行）∴∠B=∠BEF，∠D=∠DEF（两直线平行，内错角相等）∵∠BEF+ ∠BED =∠DEF∴ ∠B+∠BED=∠D
∠B+∠D+∠BED=360°
∠D+∠BED= ∠B
∠B+∠BED= ∠D
如图，AB∥ CD，试说明∠ABE、∠D 、∠E之间的大小关系 ______________________。
类型二：含多个拐点的平行线问题。
2.如图，直线l1∥ l2，∠α=∠β，∠1=40°，则∠2=______。
解：延长CD交直线l2于点E∵l1∥ l2 ∴∠3=∠1=40°∵∠α=∠β∴AB∥ CD∴∠2+∠3=180°∴∠2=180°-∠3=180°-40°=140°
2.如图，若 AB// CD，∠ BEF=70°，则∠ ABE+∠ EFC+∠ FCD 的度数是 （ ）A．215° B．250° C．320° D．无法知道
3.如图，直线AB∥ CD，∠EFA=30°，∠FGH=90°，∠HMN=30°，∠CNP=50°，则∠GHM的度数为_______。