人教版七年级下册5.3.1 平行线的性质优质课件ppt

这是一份人教版七年级下册5.3.1 平行线的性质优质课件ppt，共21页。PPT课件主要包含了新课引入，练习巩固，命题的构成，此命题分成两部分，已知项，由已知项推出的事项，知识精讲，假命题，真命题，基本知识等内容，欢迎下载使用。
1.了解命题、真命题、假命题、定理的含义，会区分命题的题设和结论。2.通过命题的真假，培养分类思想。3.通过命题的构成，培养学生分析法。
1.命题、定理的概念。2.区分命题的题设和结论。
1.区分命题的题设和结论。2.会把一些简单命题改写成“如果……那么…… ”的形式。
1.如果两条直线都与第三条直线平行，那么这两条直线也互相平行。2.等式两边加同一个数，结果仍是等式。3.对顶角相等。
以上语句都是对一件事情作出“是”或“不是”的判断。
1.画线段AB= CD。2.点P在直线AB外。3.对顶角相等吗？
以上语句没有对事情作出“是”或“不是”的判断，只是对事情进行了描述。
命题的定义 判定一件事情的语句，叫做命题。
4.两条直线相交有几个交点？
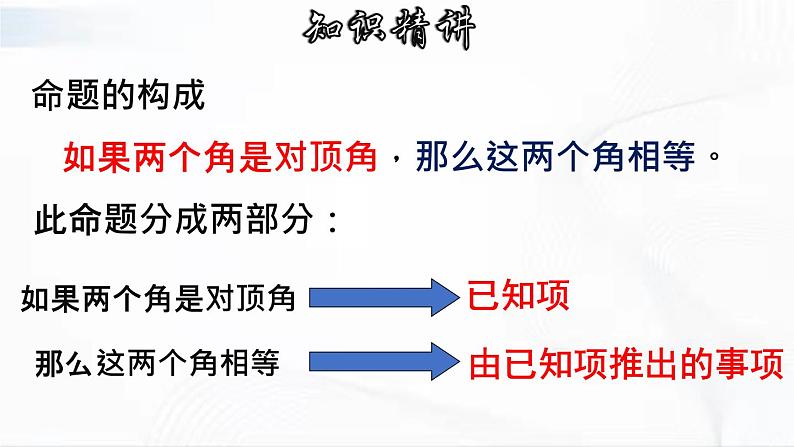
如果两个角是对顶角，那么这两个角相等。
命题的构成 命题由题设和结论组成。题设是已知项，结论是由已知项推出的事项。
两直线平行，同位角相等。
1.如果两条平行线被第三条直线所截，那么同旁内角互补。
指出下列命题的题设和结论
2.如果a > b ，b > c，那么a > c。
3.如果等式两边加同一个数，那么结果仍是等式。
“两条平行线被第三条直线所截，内错角相等”可以写成“如果两条平行线被第三条直线所截，那么内错角相等”。
命题的书写形式 数学中的命题常可以写成“如果……那么……”的形式，这时“如果”后接的部分是题设，“那么”后接的部分是结论。
把下列命题改写成“如果……那么……”的形式：
（1）垂直于同一直线的两直线平行；
（2）如果两个角是对顶角，那么这两个角相等。
（1）如果两条直线垂直于同一条直线，那么这两条直线平行；
下列语句是命题吗？它们的共同特点是什么？
（1）如果两个角互补，那么它们是邻补角；（2）如果一个数能被2整除，那么它也能被4整除。
这两个语句都是命题，它们的共同特点是题设成立时，不能保证结论一定成立，它们都是错误的命题。像这样的命题叫做假命题。
命题的分类真命题：如果题设成立，那么结论一定成立，这样的命题叫做真命题.假命题：如果题设成立时，不能保证结论一定成立，这样的命题叫做假命题.
下列命题，哪些是真命题，哪些是假命题：
（2）如果∠1= ∠2，∠2= ∠3，那么∠1= ∠3；
（3）若xy=0，则x=0；
（4）大于直角的角是钝角.
（1）如果AC=BC，那么C是线段AB的中点；
1.定理的概念 一些命题的正确性是经过推理证实的，这样得到的真命题叫做定理。
2.定理的作用 定理可以作为推理的依据。
基本事实和定理都可以作为推理的依据。
证明的概念 一个命题的正确性需要经过推理，才能作出判断，这个推理过程叫做证明。
命题“在同一平面内，如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条”是真命题吗？如果是，说明理由，如果不是，请举出反例。
如图，已知直线b∥c，a⊥b。求证a⊥c。
证明： ∵a⊥b（已知）, ∴∠1=90º（垂直定义） 又b∥c（已知） ∴∠1=∠2（两直线平行，同位角相等） ∴∠2=∠1=90º（等量代换） ∴a⊥c（垂直的定义）
在下面括号内，填上推理的根据。已知：如图，AB⊥BC，BC⊥CD，且∠1=∠2。求证：BE∥CF。证明： ∵AB⊥BC，BC⊥CD（已知） ∴ = =90°（ ） ∵∠1=∠2（已知） ∴ = （等式性质） ∴BE∥CF（ ）
内错角相等，两直线平行
1.命题的定义