人教版九年级上册24.3 正多边形和圆授课ppt课件

这是一份人教版九年级上册24.3 正多边形和圆授课ppt课件，共26页。PPT课件主要包含了一正多边形定义，弧相等，多边形是正多边形，正多边形的性质，典例解析，边心距，∠AOB，画正多边形的方法，正多边形的画法，拓展练习等内容，欢迎下载使用。
观察这些美丽的图案，都是在日常生活中，我们经常能看到的利用正多边形得到的物体。你能从图案中找出正多边形吗？你知道正多边形和圆有什么关系吗？
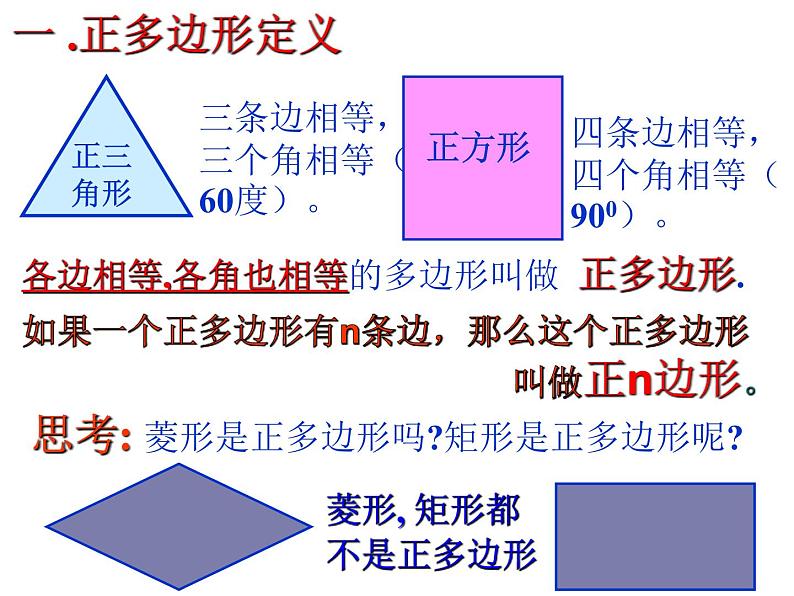
各边相等,各角也相等的多边形叫做 正多边形.
三条边相等，三个角相等（60度）。
四条边相等，四个角相等（900）。
如果一个正多边形有n条边，那么这个正多边形 叫做正n边形。
思考: 菱形是正多边形吗?矩形是正多边形呢?
菱形, 矩形都不是正多边形
二、正n边形与圆的关系
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢？
思考1: 把一个圆4等分, 并依次连 接这些点,得到正多边形吗??
弦相等（多边形的边相等）
圆周角相等（多边形的角相等）
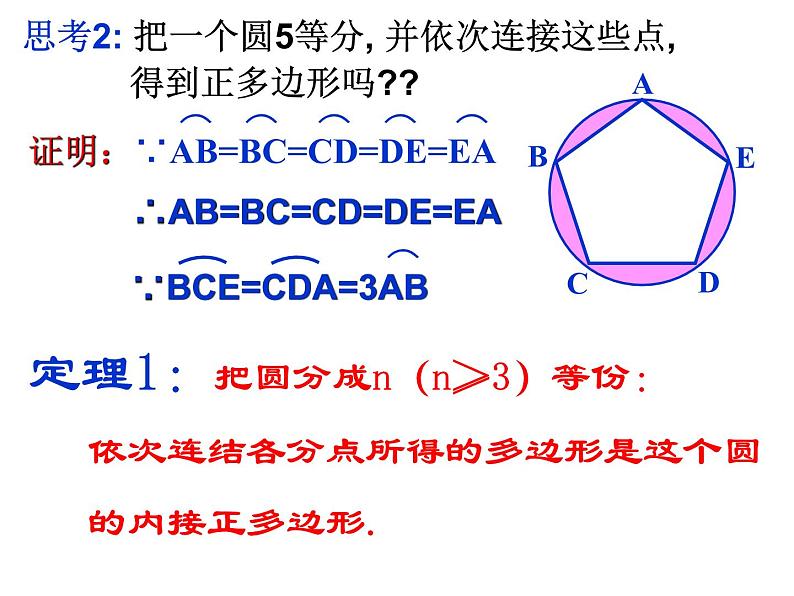
思考2: 把一个圆5等分, 并依次连接这些点, 得到正多边形吗??
证明：∵AB=BC=CD=DE=EA
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
同理∠B=∠C=∠D=∠E
∴∠A=∠B=∠C=∠D=∠E
又∵顶点A、B、C、D、E都在⊙O上
∴五边形ABCDE是⊙O的 内接正五边形.
定理1：把圆分成n（n≥3）等份： 依次连结各分点所得的多边形是这个圆 的内接正多边形.
1、正多边形的各边相等
2、正多边形的各角相等
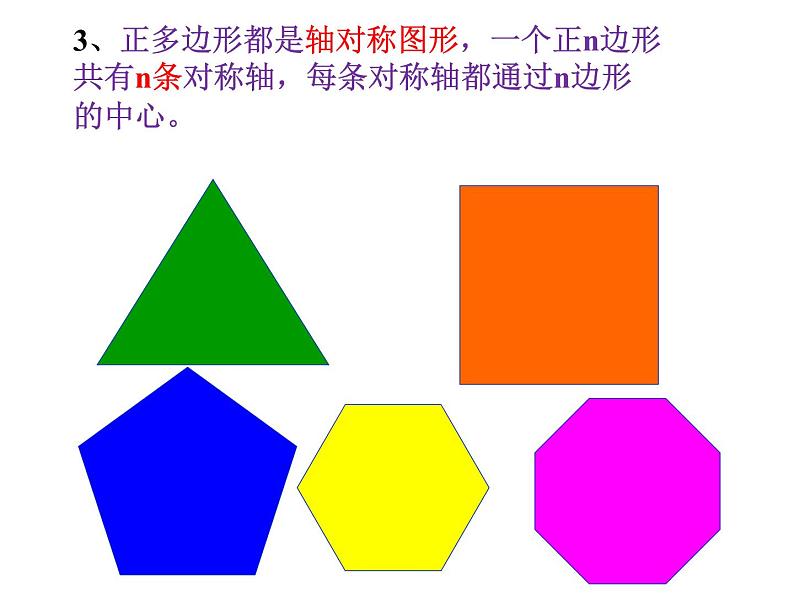
3、正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过n边形的中心。
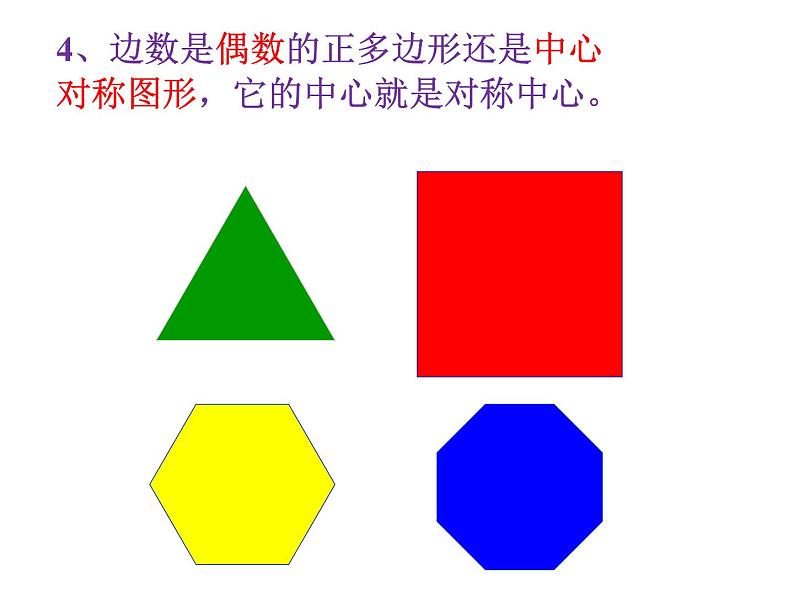
4、边数是偶数的正多边形还是中心对称图形，它的中心就是对称中心。
1、正多边形的中心:一个正多边形的外接圆的圆心.
2、正多边形的半径: 外接圆的半径
3、正多边形的中心角: 正多边形的每一条 边所对的圆心角.
4、正多边形的边心距： 中心到正多边形的一边 的距离.
四、正多边形的有关概念
边心距把△AOB分成2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
五、正多边形的有关计算
正n边形的一个内角的度数是____________;中心角是___________;正多边形的中心角与外角的大小关系是________.
有一个亭子它的地基是半径为4m的正六边形, 求地基的周长和面积(精确到0.1平方米).
∴亭子的周长 L=6×4=24(m)
归纳：正多边形的有关计算一般转化为直角三角形的问题，再利用勾股定理计算，一般步骤为：①根据题意画出图形；@求出中心角；③ 构造直角三角形求解，
1. O是正△ABC的中心，它是△ABC的_____ 圆与________圆的圆心。
OB叫正△ABC的_____, 它是正△ABC的______圆 的半径。 　　　　　
OD叫作正△ABC______, 它是正△ABC的______ 圆的半径。
∠BOC是正△ABC的_______;
∠BOC=_____度; ∠BOD=_____度.
2、正方形ABCD的外接圆圆心O叫做 正方形ABCD的____________
正方形ABCD的内切圆的半径OE叫做 正方形ABCD的___________
3、⊙O是正五边形ABCDE的外接圆，弦AB的 弦心距OF叫正五边形ABCDE的________， 它是正五边形ABCDE的________圆的半径。
∠AOB叫做正五边形ABCDE的_______角， 它的度数是________
4、图中正六边形ABCDEF的中心角是_______; 它的度数是_________;
你发现正六边形ABCDEF的半径与边长具有 什么数量关系？为什么？　
完成下表中正多边形的计算(把计算结果填入表中)：
5、正多边形的有关计算
1.用量角器等分圆2.尺规作图等分圆
(1)正四、正八边形的尺规作图
（2）正六、正三 、正十二边形的尺规作图
由于正多边形在生产、生活实际中有广泛的应用性，所以会画正多边形应是学生必备能力之一。 怎样画一个正多边形呢？ 问题1：已知⊙O的半径为2cm，求作圆的内接正三角形.
①用量角器度量，使∠AOB=∠BOC=∠COA=120°． ②用量角器或30°角的三角板度量，使∠BAO=∠CAO=30°．
你能用以上方法画出正四边形、正五边形、正六边形吗？
你能尺规作出正四边形、正八边形吗？
只要作出已知⊙O的互相垂直的直径即得圆内接正方形，再过圆心作各边的垂线与⊙O相交，或作各中心角的角平分线与⊙O相交，即得圆接正八边形，照此方法依次可作正十六边形、正三十二边形、正六十四边形……
1、两个正六边形的边长分别是3和4，这两个正六边形的面积之比等于________2．圆内接正方形的半径与边长的比值是________3．圆内接正四边形的边长为4 cm，那么边心距是________4．已知圆内接正方形的边长为，则该圆 的内接正六边形边长为__________．5． 圆内接正六边形的边长是8 cm，那么该正六边形的半径为________；边心距为________．
6、已知正多边形的边心距与边长的比是，则此正多边形是( ) A．正三角形 B、正方形 C．正六边形 D正十二边形7．以下有四种说法：①顺次连结对角线相等的四边形各边中点，则所得的四边形是菱形；②等边三角形是轴对称图形，但不是中心对称图形；③顶点在圆周上的角是圆周角；④边数相同的正多边形都相似，其中正确的有（） A．1个 B．2个 C．3个 D 4个8．正多边形的中心角与该正多边形一个内角的关系是（） A.互余 B.互补 C.互余或互补 D.不能确定