

所属成套资源:2021年人教版数学七年级上册期末复习专题练习(含答案)
2021年人教版数学七年级上册期末复习《与角有关的计算》专题练习(含答案)
展开这是一份2021年人教版数学七年级上册期末复习《与角有关的计算》专题练习(含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021年人教版数学七年级上册期末复习
《与角有关的计算》专题练习
一、选择题
1.将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
A.140° B.160° C.170° D.150°
2.已知∠AOB=60°,在∠AOB内取一点C,引射线OC,若∠AOC是∠BOC的,
则∠AOC为( )
A.20° B.24° C.36° D.40°
3.如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
4.如图,直线AB、CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
A.38° B.104° C.142° D.144°
5.如图,∠AOC,∠BOD都是直角,∠AOD:∠AOB=3:1,则∠BOC的度数是( )
A.22.5° B.45° C.90° D.135°
6.已知∠1与∠2互余,∠2与∠3互补,∠1=58°,则∠3=( )
A.58° B.148° C.158° D.32°
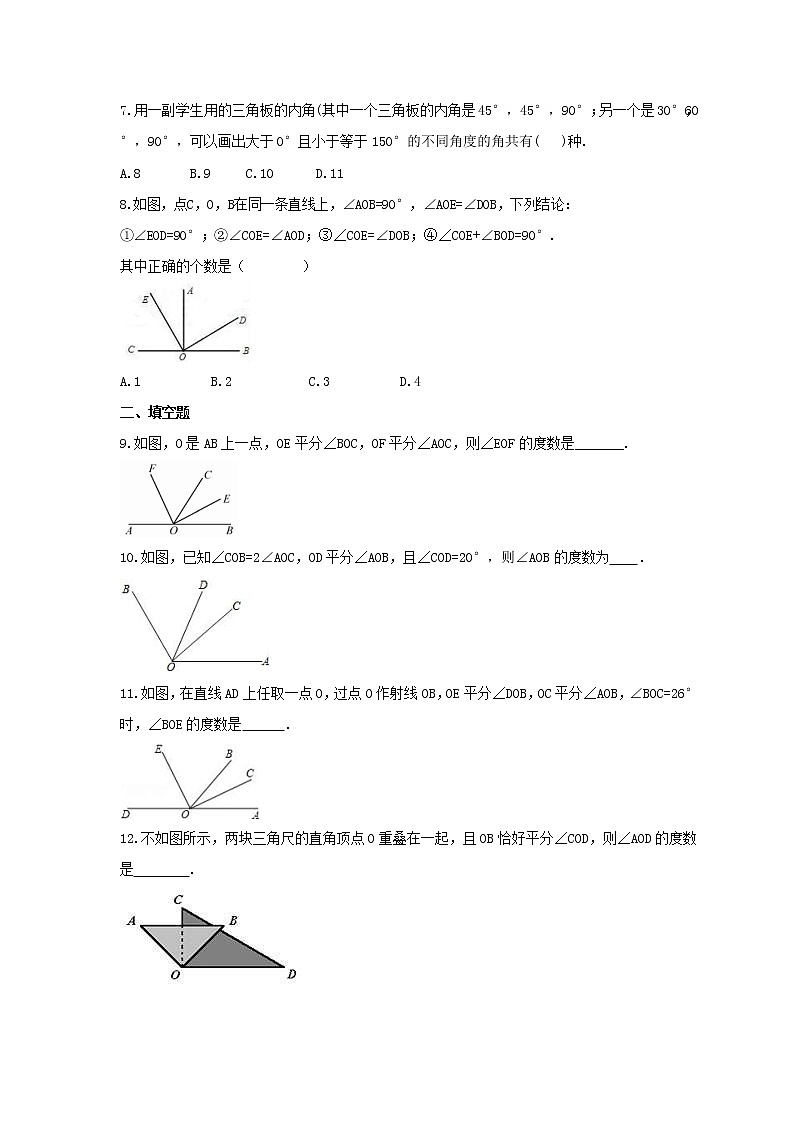
7.用一副学生用的三角板的内角(其中一个三角板的内角是45°,45°,90°;另一个是30°,60°,90°,可以画出大于0°且小于等于150°的不同角度的角共有( )种.
A.8 B.9 C.10 D.11
8.如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列结论:
①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;④∠COE+∠BOD=90°.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
9.如图,O是AB上一点,OE平分∠BOC,OF平分∠AOC,则∠EOF的度数是_______.
10.如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为 .
11.如图,在直线AD上任取一点O,过点O作射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,∠BOE的度数是 .
12.不如图所示,两块三角尺的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是 .
13.如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°,则∠AOF的度数为 °.
14.用一副三角板可以直接得到30°,45°,60°,90°四种角,利用一副三角板可以拼出另外一些特殊角,如75°,120°等,请拼一拼,使用一副三角板还能拼出哪些小于平角的角,这些角的度数是:______.
三、解答题
15.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
16.如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=29°.求∠AOB的度数.
17.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
18.如图,已知∠AOE是平角,∠DOE=20°,OB平分∠AOC,且∠COD:∠BOC=2:3,求∠BOC的度数.
19.如图1,已知∠AOB=150°,∠AOC=40°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=10°,则∠COF=________;
(2) 若∠COF=20°,则∠EOB=____________;
(3) 若∠COF=n°,则∠EOB=_____(用含n的式子表示).
(4) 当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
20.(1)如图,一个直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C,△ABC中,若∠A=30°,则∠ABC+∠ACB=__150°__,∠XBC+∠XCB=____;
(2)若改变直角三角板XYZ的位置,但三角板XYZ的两条直角边XY,XZ仍然分别经过B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.
21.已知点O是直线AB上一点,∠COE=90°,OF是∠AOE的平分线,
(1)当点C、E、F在直线AB的同侧(如图①所示)时,试说明∠BOE=2∠COF;
(2)当点C与点E、F在直线AB的两旁(如图②所示)时,(1)中的结论是否仍然成立?
请给出你的结论,并说明理由。
(3)将如图②中的射线OF绕O点顺时针旋转m°(0<m<180),得到射线OD,
设∠AOC=n°,若∠BOD=°,则∠DOE的度数是多少?(用含n的式子表示)
22.如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线。
(1请写出图中所有∠EOC的补角 ;
(2)如果∠POC:∠EOC=2:5.求∠BOF的度数。
23.如图,∠AOB=90°,∠AOC为∠AOB外的一个锐角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1),(2),(3)的结果中,你能看出什么规律?
(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法.请你模仿(1)~(4)设计一道以线段为背景的计算题,并写出其中的规律.
24.已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当∠AOC=40°,点C、E、F在直线AB的同侧(如图1所示)时,求∠BOE和∠COF的度数.
(2)当∠AOC=40°,点C与点E、F在直线AB的两旁(如图2所示)时,求∠BOE和∠COF的度数.
(3)当∠AOC=n°,请选择图(1)或图(2)一种情况计算,
∠BOE=
∠COF= (用含n的式子表示)
(4)根据以上计算猜想∠BOE与∠COF的数量关系 (直接写出结果).
参考答案
1.答案为:B.
2.答案为:B
3.答案为:C
4.答案为:C
5.答案为:B
6.答案为:B
7.答案为:C.
8.答案为:C
9.答案为:90°
10.答案为:120°.
11.答案为:64°
12.答案为:135°
13.答案为:30度;
14.答案为:15°,105°,135°,150°,165°;
15.解:(1)图中小于平角的角:
∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB.
(2)∵∠AOC=50°,OD平分∠AOC,
∴∠DOC=1/2∠AOC=25°,∠BOC=180°-∠AOC=130°,
∴∠BOD=∠DOC+∠BOC=155°.
(3)∵∠DOE=90°,∠DOC=25°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°.
又∵∠BOE=∠BOD-∠DOE=155°-90°=65°,
∴∠COE=∠BOE,
即OE平分∠BOC.
16.答案略
17.因为∠AOD=∠AOC-∠DOC=60°-∠DOC,
∠BOC=∠BOD-∠DOC=90°-∠DOC,
所以∠AOB=∠AOD+∠COD+∠BOC
=60°-∠DOC+∠DOC+90°-∠DOC
=150°-∠DOC,
所以150°-∠DOC=3∠DOC,
所以∠DOC=37.5°,
所以∠AOB=3×37.5°=112.5°.
18.解:设∠COD=2x°,则∠BOC=3x°.
因为OB平分∠AOC,所以∠AOB=3x°.
所以2x+3x+3x+20=180.解得x=20.
所以∠BOC=3×20°=60°.
19.(1)∵∠AOB=150°,∠EOB=10°, ∴∠AOE=∠AOB-∠EOB=150°-10°=140°,
∵OF平分∠AOE, ∴∠AOF==70°,
∴∠COF=∠AOF-∠AOC=70°-40°=30°;
(2)∵∠AOC=40°,∠COF=20°, ∴∠AOF=∠AOC+∠COF=40°+20°=60°,
∵OF平分∠AOE, ∴∠AOE=2∠AOF=2×60°=120°,
∴∠EOB=∠AOB-∠AOE=150°-120°=30°;
(3)∵∠AOC=40°,∠COF=n°, ∴∠AOF=∠AOC+∠COF=40°+n°=60°,
∵OF平分∠AOE, ∴∠AOE=2∠AOF=2(40°+n°)=80°+2n°,
∴∠EOB=∠AOB-∠AOE=150°-(80°+2n°)=70°-2n°;
故答案为:30°,30°,70°-2n°;
(4)如图所示;∠EOB=70°+2∠COF.
证明:设∠COF=n°,则∠AOF=∠AOC-∠COF=40°-n°,
又∵OF平分∠AOE,∴∠AOE=2∠AOF=80°-2n°.
∠EOB=∠AOB-∠AOE=150°-(80°-2 n°)=(70+2n)°即∠EOB=70°+2∠COF.
20.答案为:90°
21.(1)如图①,设∠COF=α,则∠EOF=90°-α
因为,OF是∠AOE的平分线,∠AOF=∠EOF=90°-α
所以,∠AOC=(90°-α)- α=90°-2α
∠BOE=180°-∠COE-∠AOC =180°-90°-(90°-2α) =2α,
即∠BOE=2∠COF;
(2)成立。如图②,设∠AOC=β,则∠AOF=,
所以∠COF=∠AOC+∠AOF=β+=(90°+β)
而∠BOE=180°-∠AOE= 180°-(90°-β)=90°+β,
即∠BOE=2∠COF;
(3)因为∠DOE=180°-∠AOE-∠BOD
=180°-(90°-n°)- °=°
22.(1)∠EOD, ∠AOF-(2)∠BOF=50°
23.解:(1)因为∠AOB=90°,∠AOC=30°,所以∠BOC=120°.
因为OM平分∠BOC,所以∠COM=∠BOC=60°.
因为ON平分∠AOC,所以∠CON=∠AOC=×30°=15°,
所以∠MON=∠COM-∠CON=60°-15°=45°
(2)当∠AOB=α,其它条件不变时,仿(1)可得∠MON=α
(3)仿(1)可求得∠MON=∠COM-∠CON=45°
(4)从(1)(2)(3)的结果中,可以得出一般规律:∠MON的大小总等于∠AOB的一半,与锐角∠AOC的大小无关
(5)问题可设计为:已知:线段AB=a,延长AB到点C,使BC=6,点M,N分别为AC,BC的中点,求MN的长.
规律是:MN的长度总等于AB的长度的一半,而与BC的长度无关
24.解:(1)如图(1),∵∠AOC=40°,∠COE是直角,∴∠AOE=130°,∴∠BOE=180°﹣130°=50°,又∵OF平分∠AOE,∴∠AOF=∠AOE=65°,∴∠COF=65°﹣40°=25°;
(2)如图(2),∵∠AOC=40°,∠COE是直角,∴∠AOE=50°,∴∠BOE=180°﹣50°=130°,
又∵OF平分∠AOE,∴∠AOF=∠AOE=25°,∴∠COF=25°+40°=65°;
(3)如图(2),∵∠AOC=n°,∠COE是直角,∴∠AOE=(90﹣n)°,
∴∠BOE=180°﹣(90﹣n)°=(90+n)°,
又∵OF平分∠AOE,∴∠AOF=∠AOE=(45﹣n)°,∴∠COF=n°+(45﹣n)°=45°n°;
故答案为:(90+n)°,45°n°;
(4)根据以上计算的∠BOE和∠COF的度数可得:∠BOE=2∠COF.故答案为:∠BOE=2∠COF.
相关试卷
这是一份中考数学三角形有关角的计算练习,共5页。
这是一份【专题训练】人教版数学七年级上册 第4章《几何图形初步》9 角的有关计算 练习(pdf版,含答案),文件包含同步培优-导学案+专题训练参考答案全册pdf、第4章《几何图形初步》专题训练9角的有关计算pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
这是一份【专题训练】人教版数学七年级上册 第4章《几何图形初步》8 线段的有关计算 练习(pdf版,含答案),文件包含同步培优-导学案+专题训练参考答案全册pdf、第4章《几何图形初步》专题训练8线段的有关计算pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。












