小学数学人教版六年级下册5 数学广角 （鸽巢问题）课文课件ppt

这是一份小学数学人教版六年级下册5 数学广角 （鸽巢问题）课文课件ppt，文件包含51《鸽巢原理》教学PPTpptx、第5单元第1课时《鸽巢原理》导学案设计docx、第5单元第1课时《鸽巢原理》教案设计docx等3份课件配套教学资源，其中PPT共19页， 欢迎下载使用。
我给大家表演一个“魔术”。一副牌，取出大小王，还剩52张牌，你们5人每人随意抽一张，我知道至少有2张牌是同花色的。相信吗？
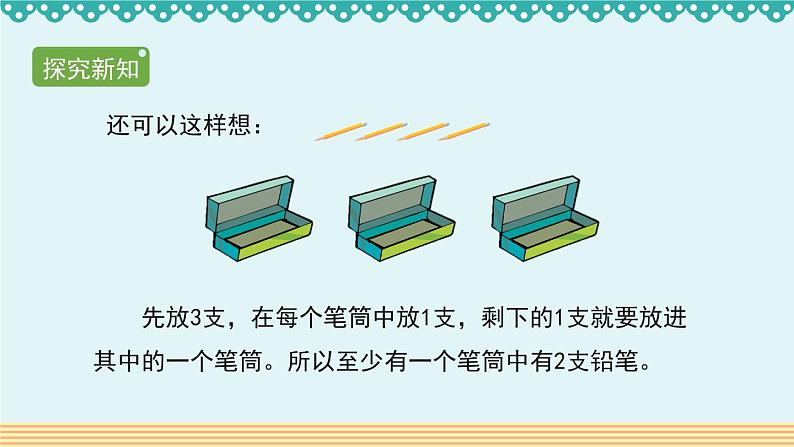
把4支铅笔放进3个笔筒中，不管怎么放，总有一个笔筒里至少有2支铅笔。
“总有”和“至少”是什么意思？
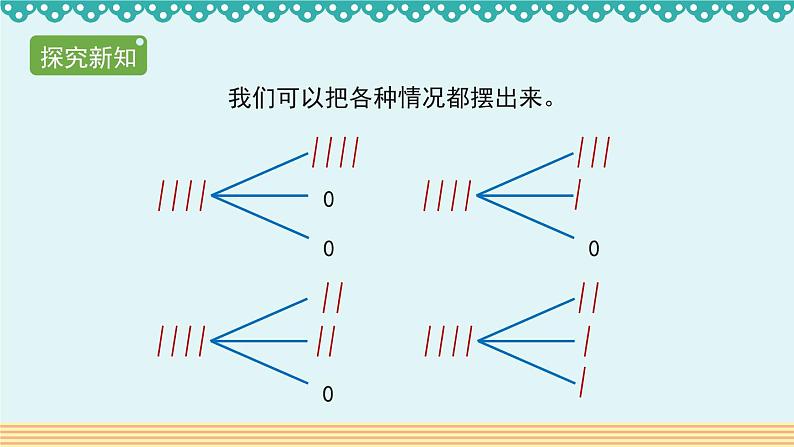
先独立思考：(1)可以怎么放？(2)共有几种不同放法？再小组内交流，全班总结。
我们可以把各种情况都摆出来。
先放3支，在每个笔筒中放1支，剩下的1支就要放进其中的一个笔筒。所以至少有一个笔筒中有2支铅笔。
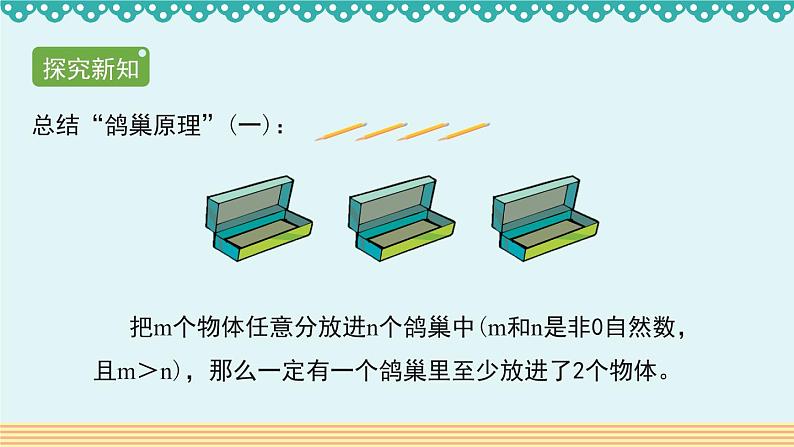
总结“鸽巢原理”(一)：
把m个物体任意分放进n个鸽巢中(m和n是非0自然数，且m＞n)，那么一定有一个鸽巢里至少放进了2个物体。
把7本书放进3个抽屉，不管怎么放，总有一个抽屉里至少放进3本书。为什么？
两种放法都有一个抽屉放了3本或多于3本，所以不管怎么放，总有一个抽屉里至少放进3本书。
我随便放放看，一个抽屉1本，一个抽屉2本，一个抽屉4本。
如果每个抽屉最多放2本，那么3个抽屉最多放6本，可题目要求放的是7本书。所以还要往其中的一个抽屉里放1本。
借鉴数的分解思路来思考
不管怎样放，总有一个抽屉里至少放进3本书。
不管怎样放，总有一个抽屉至少放进3本书。
如果有8本书会怎样呢？10本书呢？
答：如果一共有8本书，总有一个抽屉至少放3本书。
答：如果一共有10本书，总有一个抽屉至少放4本书。
总结“鸽巢原理”(二)：
　　把多于kn个的物体任意分放进n个鸽巢中(k和n是非0自然数)，那么一定有一个鸽巢里至少放进了(k＋1)个物体。
1.5只鸽子飞进了3个鸽笼，总有一个鸽笼至少飞进了2只鸽子。为什么？
2.你理解上面扑克牌魔术的道理了吗？
　　一副扑克牌共54张，去掉两张王牌，剩下方块、红桃、梅花、黑桃四种花色各13张。我们把4种花色看成“4个鸽巢”，把5张扑克牌放进“4个鸽巢”中，必然有一个鸽巢至少放进2张扑克牌，即至少有2张牌是同花色的。
2.11只鸽子飞进了4个鸽笼，总有一个鸽笼至少飞进了3只鸽子。为什么？
3．5个人坐4把椅子，总有一把椅子上至少坐2人，为什么？
把5个人分到“4个房间”(代表4把椅子)中，5÷4＝1……1，所以一定有“一个房间”至少有1＋1＝2(人)，即总有一把椅子上至少坐2人。
通过今天的学习，你们有哪些收获？