高考数学专项解题方法归纳探究（全国通用）模板14 抛物线与方程（解析版）

这是一份高考数学专项解题方法归纳探究（全国通用）模板14 抛物线与方程（解析版），共10页。试卷主要包含了利用抛物线的性质求面积或长度等内容，欢迎下载使用。
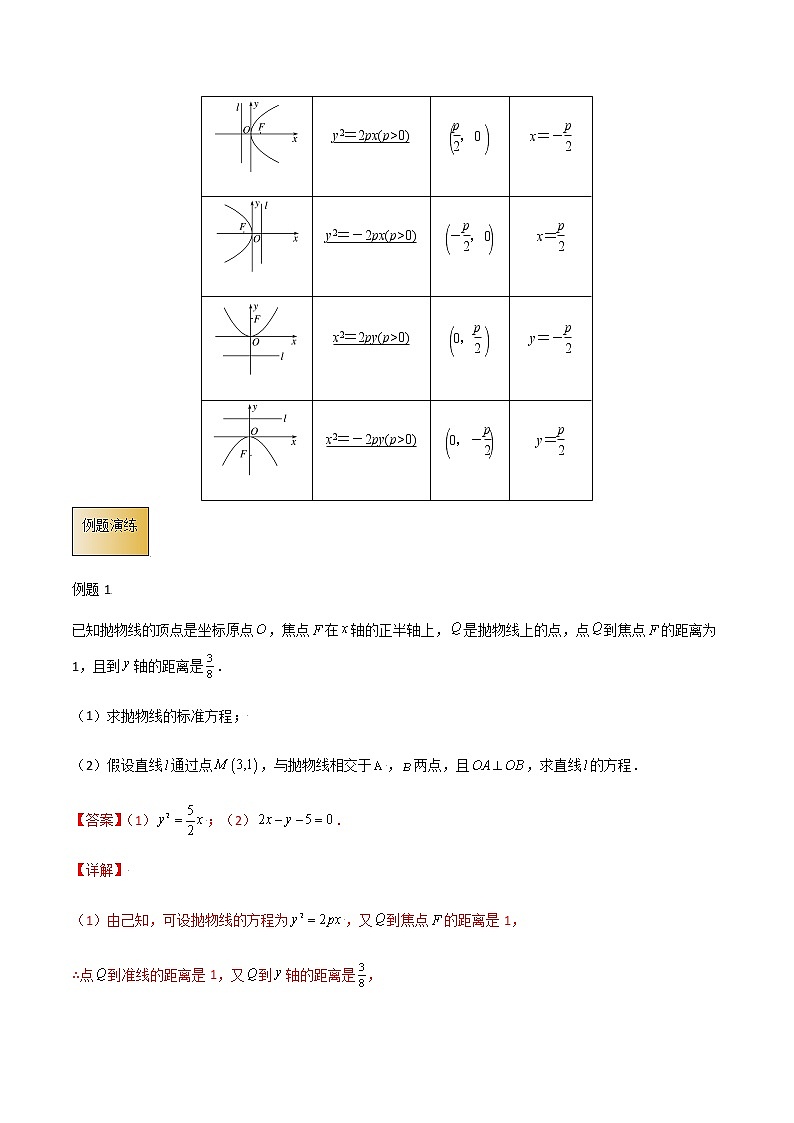
学校:___________姓名：___________班级：___________考号：___________模板一、求抛物线的标准方程及定义的应用问题1.模板解决思路求抛物线的标准书程时，首先确定标准方程的类型，并将其用有关参数p表示出来,然后再结合问题的条件，建立参数p满足的等式,求得p的值，再代人所设方程，即一定位，二定量,最后写过程2.模板解决步骤①第一步；明确抛物线的类 型，并设出相应的抛物线方程.②第二步；结合已知条件求 出参数的值.③第三步；写出抛物线方程.④第四步；结合抛物线的定义求得结论知识点一　抛物线的定义1．定义：平面内与一定点F和一条定直线l(不经过点F)距离相等的点的轨迹．2．焦点：定点F.3．准线：定直线l.知识点二　抛物线的标准方程图形标准方程焦点坐标准线方程y2＝2px(p>0)x＝－y2＝－2px(p>0)x＝x2＝2py(p>0)y＝－x2＝－2py(p>0)y＝例题1已知抛物线的顶点是坐标原点，焦点在轴的正半轴上，是抛物线上的点，点到焦点的距离为1，且到轴的距离是．（1）求抛物线的标准方程；（2）假设直线通过点，与抛物线相交于，两点，且，求直线的方程．【答案】（1）；（2）．【详解】（1）由己知，可设抛物线的方程为，又到焦点的距离是1，∴点到准线的距离是1，又到轴的距离是，∴，解得，则抛物线方程是．（2）假设直线的斜率不存在，则直线的方程为，与联立可得交点、的坐标分别为，，易得，可知直线与直线不垂直，不满足题意，故假设不成立，∴直线的斜率存在．设直线为，整理得，设，，联立直线与抛物线的方程得，消去，并整理得，于是，，∴，又，因此，即，∴，解得或．当时，直线的方程是，不满足，舍去．当时，直线的方程是，即，∴直线的方程是．例题2已知面积为16的等腰直角(为坐标原点)内接于抛物线，，过抛物线的焦点且斜率为2的直线与该抛物线相交于，两点，点是的中点.（1）求此抛物线的方程和焦点的坐标；（2）若焦点在轴上的椭圆经过点，其离心率，求椭圆的标准方程.【答案】（1）抛物线的方程为，焦点的坐标为；（2）【详解】（1）为等腰直角三角形，且，则由抛物线的对称性可得轴，则可设，则，解得，即代入抛物线，可得，解得，则抛物线的方程为，焦点的坐标为；（2）由题可得直线的方程为，联立直线与抛物线方程得，设，则，又是的中点，则可得，设椭圆方程为，，即，又，可得，则方程为，将代入，可得，解得，则椭圆方程为.模板二、利用抛物线的性质求面积或长度1.模板解决思路在使用抛物线的几何性质解决问题时，一定要区分抛物线的开口方向，根据不同的开口方向来确定其几何性质2.模板解决步骤①第一步；设未知数，根据已知条件,结合抛勿线的性质列方程(组).②第二步；解方程(组)，并求出相关的量.③第三步；代人相关量,求得面积或长度.知识点一　抛物线的简单几何性质标准方程y2＝2px(p>0)y2＝－2px(p>0)x2＝2py(p>0)x2＝－2py(p>0)图形范围x≥0，y∈Rx≤0，y∈Ry≥0，x∈Ry≤0，x∈R对称轴x轴x轴y轴y轴焦点坐标FFFF准线方程x＝－x＝y＝－y＝顶点坐标O(0,0)离心率e＝1通径长2p知识点二、三个要点确定抛物线的简单几何性质(1)开口：由抛物线标准方程看图象开口，关键是看准二次项是x还是y，一次项的系数是正还是负．(2)关系：顶点位于焦点与准线中间，准线垂直于对称轴．(3)定值：焦点到准线的距离为p；过焦点垂直于对称轴的弦(又称为通径)长为2p；离心率恒等于1.例题1已知为坐标原点，抛物线的准线与圆交于，两点，抛物线与圆交于，两点，且.（1）求抛物线的标准方程；（2）动点在抛物线的准线上，直线与抛物线交于，两点，直线与抛物线交于，两点，与的交点为，且.设直线，的斜率分别为，，证明：为定值.【答案】（1）；（2）证明见解析.【详解】（1）因为，所以或(舍)，又因为，所以，所以，所以抛物线的标准方程为；（2）设，，，设，联立，，所以，所以，所以，所以，联立，，所以，所以，所以，因为，所以，又，所以，所以，所以为定值.例题2已知抛物线：的焦点到直线：的距离等于.（1）求抛物线的方程及准线方程；（2）设是直线上的动点，过点作抛物线的两条切线，切点分别为､，求面积的最小值.【答案】（1）抛物线的方程为，准线方程为；（2）最小值为.【详解】（1）由题意知抛物线的焦点，∴，∴，∵，∴，∴抛物线的方程为，准线方程为.（2）设，，，则切线的方程为，同理切线的方程为，分别代入点可得，直线的方程为：.由，消去x得，所以，∴，点到直线的距离为，∴，，而，∴.当且仅当，即时，的最小值为.