数学九年级上册24.1.4 圆周角背景图课件ppt

这是一份数学九年级上册24.1.4 圆周角背景图课件ppt，共18页。PPT课件主要包含了合作探究，知识点一，知识点二，∠ACB，∠AOB，∠A∠C，精炼提升，知识点三，COA，同弧或等弧等内容，欢迎下载使用。

问题1、什么是圆心角？ 问题2、圆心角、弦、弧之间有什么内在联系？
把顶点在圆心的角叫做圆心角
在同圆或等圆中：（1）相等的圆心角所对的弧、弦也相等；（2）如果两条弧相等，那么他们所对的圆心角、弦相等；（3）如果两条弦相等，那么他们所对的圆心角、弧相等；
理解圆周角的定理，理解圆周角定理的推论.
问题1、顶点在 ，并且两边都与圆 的角叫做圆周角．问题2、圆周角定义的两个特征：（1）顶点都在 ；（2）两边都与圆 ．

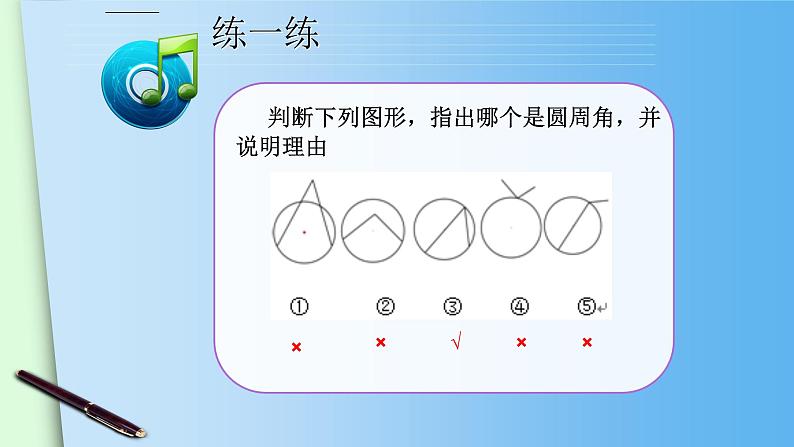
判断下列图形，指出哪个是圆周角，并说明理由
思考：如图， 所对的圆周角是 ，所对的圆心角是 .做一做：用量角器度量它们的度数，发现它们有什么关系？在⊙O上任取一条弧，做出这条弧所对的圆周角和圆心角，有同样的结论吗？猜想：弧所对的圆周角等于它所对的圆心角的 。
思考：在⊙O任取一个圆周角∠BAC，则圆心O与圆周角的位置，会出现几种情况？
①在圆周角的一条边上（如图1）圆心O在∠BAC的一条边上.∵OA=OC∴ .∵∠BOC=∠A+∠C∴∠BOC=∠A+∠A 即： .
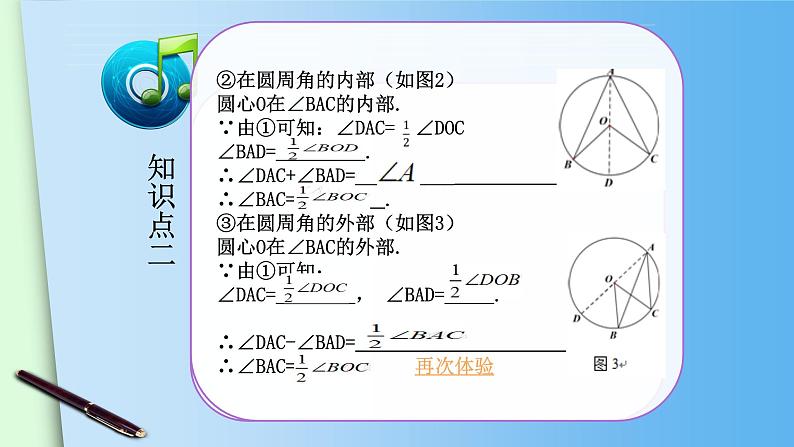
②在圆周角的内部（如图2）圆心O在∠BAC的内部.∵由①可知：∠DAC= ∠DOC∠BAD= .∴∠DAC+∠BAD=__________ ∴∠BAC= .③在圆周角的外部（如图3）圆心O在∠BAC的外部.∵由①可知：∠DAC= ， ∠BAD= .∴∠DAC-∠BAD= ______ ∴∠BAC= . 再次体验
圆周角的定理： 一条弧所对的圆周角等于它所对圆心角的一半。
几何语言：∵∠AOB是 所对的圆心角， ∠ACB是 所对的圆周角∴ ∠AOB = 2∠ACB
1、如图，已知在⊙ O 中，∠BOC =150°，求∠A
2、如图，∠A是圆O的圆周角，∠A=40°，求∠OBC的度数。
3.如图，圆心角∠AOB=100°，则∠ACB=___。
4、 如图，在直径为AB的半圆中，O为圆心，C、D为半圆上的两点，∠COD=500，则∠CAD=_________
如图，OA,OB,OC都是⊙O的半径，∠AOB=2∠BOC.求证：∠ACB=2∠BAC
知识点三 圆周角定理的推论
在同圆或等圆中，同弧或等弧所对的圆周角 .已知：如图∠C和∠D是 所对的圆周角求证：∠C=∠D证明：∵∠C和∠D是 所对的圆周角且是 所对的圆心角的一半∴∠C= ，∠D= .∴ .
讨论：它的逆命题成立吗？为什么？在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定 .
圆周角的定理： 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。
1、如下左图，⊙O的直径AB垂直于弦CD，AB、CD相交于点E，∠COD＝100°，则∠COE = ，∠DOE = .2、如下右图，AB、AC、BC都是⊙O的弦，若∠CAB＝∠CBA，则∠COB=∠ ,AC= .
3、如图所示,自☉O上一点C向弦AB作垂线段CD,求证:∠ACD=∠BCO.
证明:延长CO交☉O于E点,连接BE.则∠CAB=∠CEB.∵CE为☉O的直径,∴∠CBE=90°,∴∠ADC=∠CBE=90°.∵∠CAD+∠ADC+∠ACD=180°,∠CEB+∠CBE+∠BCO=180°,∴∠ACD=∠BCO.
1、顶点在 ，并且两边都与圆 的角叫做圆周角．2、圆周角定理： .3、推论： 所对的圆周角相等. 所对的圆周角是相等；90°的圆周角所对的弦是 ．.
4、学习反思：____________________________________________________________________________.
一条弧所对的圆周角等于它所对的圆心角的一般