人教版数学七年级上册期末总复习四几何图形初步课件

展开

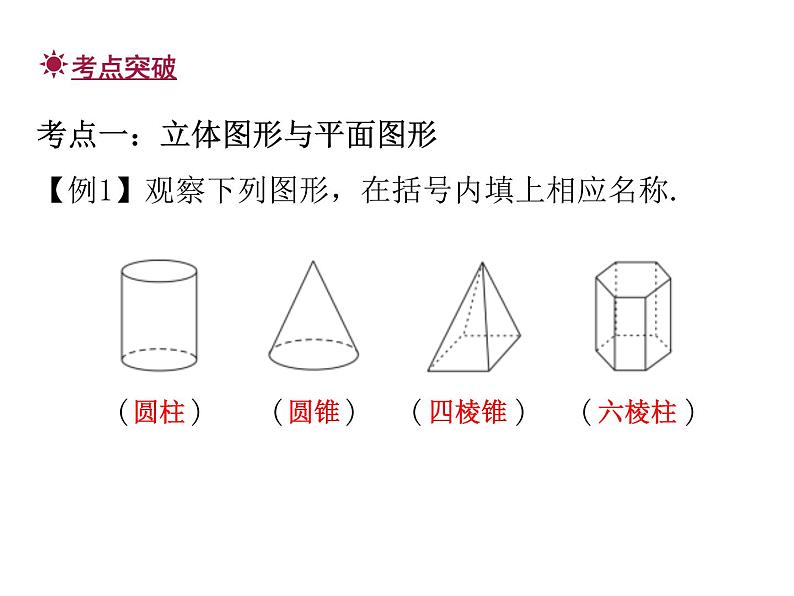
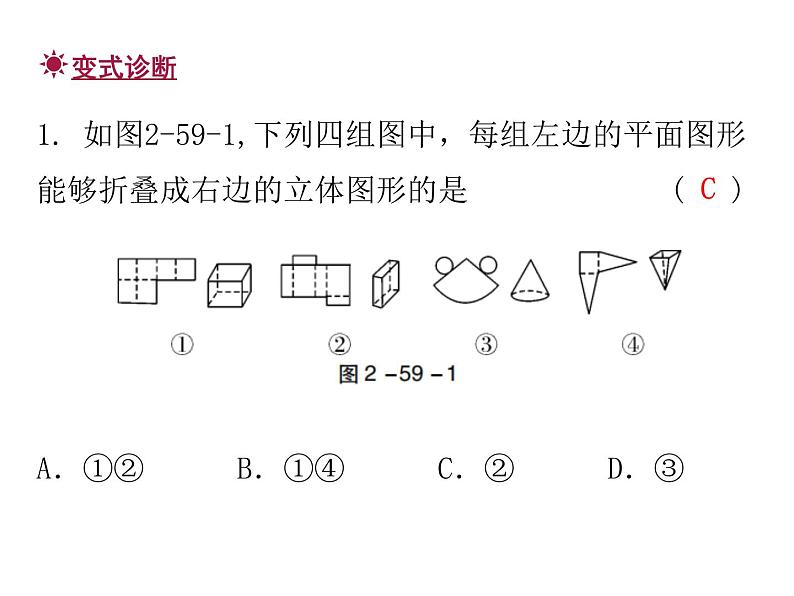
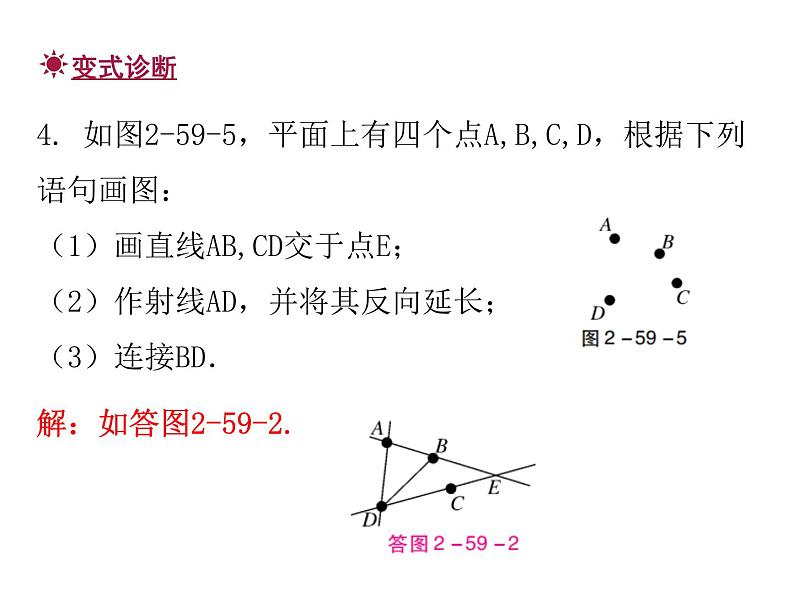
这是一份人教版数学七年级上册期末总复习四几何图形初步课件，

人教版七年级期末总复习4几何图形初步考点一：立体图形与平面图形【例1】观察下列图形，在括号内填上相应名称. ( ) ( ) ( ) ( )圆柱圆锥四棱锥六棱柱1. 如图2-59-1,下列四组图中，每组左边的平面图形能够折叠成右边的立体图形的是 ( )A．①② B．①④ C．② D．③C考点二：直线、射线、线段【例2】如图2-59-2，下列说法错误的是 ( )A．直线AC与射线BD相交于点AB．BC是线段C．直线AC经过点AD．点D在直线AB上D2. 如图2-59-3，点C是线段BD之间的点，有下列结论：①图中共有5条线段；②射线BD和射线DB是同一条射线；③直线BC和直线BD是同一条直线；④射线AB，AC，AD的端点相同.其中正确的结论是 ( )A．②④B．③④C．②③D．①③B【例3】木工师傅用两颗水泥钉就能将一根木条固定在墙壁上，这样做的数学依据是__________________.两点确定一条直线两点之间，线段最短考点三：作图【例4】如图2-59-4，已知线段a，b，作一条线段等于2（a-b）．4. 如图2-59-5，平面上有四个点A,B,C,D，根据下列语句画图：（1）画直线AB,CD交于点E；（2）作射线AD，并将其反向延长；（3）连接BD．考点四：线段的计算【例5】如图2-59-6，已知点M是线段AB的中点，点N在线段MB上，MN= AM，若MN=3 cm，求线段AB和线段NB的长．5. 如图2-59-7，线段AB=9 cm，BC=6 cm，点M是线段AC的中点．（1）线段AC=________cm，AM=________cm；（2）在线段CB上取一点N，使得CN∶NB=1∶2．求MN的长．31.5考点五：角的概念【例6】如图2-59-8，∠AOB=90°，以O为顶点的锐角共有 ( )A．6个B．5个C．4个D．3个B6. 如图2-59-9，用两种方法表示的是同一个角的 ( )A．∠1和∠CB．∠2和∠CC．∠3和∠AD．∠4和∠BD考点六：度、分、秒的换算【例7】26.5°= ______°______′．263026.8考点七：方向角【例8】如图2-59-10，已知点D在点O的西北方向，点E在点O的北偏东50°方向，那么∠DOE的度数为______度．958. 如图2-59-11，A，O，B在同一条直线上，如果OA的方向是北偏西25°，那么OB的方向是南偏东______.25°考点八：余角和补角【例9】若∠A=60°48′，则∠A的余角=__________.29°12′142【例10】已知一个角的余角比它大10°，则这个角等于________度．4050°考点九：角的计算【例11】如图2-59-12，已知∠COB=2∠AOC，OD平分∠AOB，且∠COD=18°，求∠AOB的度数．解：设∠AOC=x，则∠COB=2∠AOC=2x．因为OD平分∠AOB，所以∠AOD=∠BOD=1.5x．所以∠COD=∠AOD-∠AOC=1.5x-x=0.5x．因为∠COD=18°，所以0.5x=18°.所以x=36°.所以∠AOB=3×36°=108°．11. 如图2-59-13，已知∠AOB=155°，∠AOC=∠BOD=90°．（1）写出与∠COD互余的角；（2）求∠COD的度数；（3）图中是否有互补的角？若有，请写出来．解：（1）因为∠AOC=∠BOD=90°，所以∠COD+∠AOD=90°，∠COD+∠BOC=90°.所以与∠COD互余的角是∠AOD和∠BOC.（2）∠BOC=∠AOB-∠AOC=65°，所以∠COD=∠BOD-∠BOC=25°.（3）∠COD与∠AOB,∠AOC与∠BOD互补．12. 与红砖、足球类似的几何体分别是 ( )A．长方形、圆B．长方体、球C．长方形、球D．长方体、圆B13. 下列说法正确的是 ( )A．射线PA和射线AP是同一条射线B．射线OA的长度是10 cmC．直线AB,CD相交于点mD．两点确定一条直线D14. 在15°,65°,75°,135°的角中，能用一副三角尺画出来的有 ( )A．1个 B．2个C．3个 D．4个15. 已知∠α与∠β互补，∠α=5∠β，则∠α等于 ( )A．150° B．120°C．90° D．60°CA16. 如图2-59-14，已知点C是线段AD的中点，AB=20 cm，BD=8 cm，则BC=______ cm．17. 如图2-59-15，点O是直线AB上的点，OC平分∠AOD，∠BOD=30°，则∠AOC=______度．147518. 如图2-59-16，将一块直角三角板的直角顶点O放在直尺的一边CD上，如果∠AOC=28°，那么∠BOD=________度．6219. 如图2-59-17，已知线段AB=5，延长线段AB到点C，使BC=2AB，若点D是线段AC的中点，求线段BD的长度.解：因为∠AOB=∠3=90°，∠1∶∠3=7∶9，所以∠1=70°.因为OC是∠BOD的平分线，所以∠BOD=2∠1=140°．20. 如图2-59-18，∠AOB=90°，OC是∠BOD的平分线，若∠1∶∠3=7∶9,求∠BOD的度数．21. 如图2-59-19是小明家（图中点O）和学校所在地的简单地图，请写出图中商场、学校、停车场分别相对小明家的方向角.解：商场在小明家北偏西30°方向，学校在小明家北偏东45°方向，停车场在小明家南偏东60°方向.22. 如图2-59-20所示的正方体的展开图是 ( )A23. 已知∠A=20°18′，∠B=20°15′30″，∠C=20.25°，则度数最大的是 ( )A．∠A B．∠BC．∠C D．无法确定A24. 一副三角板按如图2-59-21方式摆放，且∠1的度数比∠2的度数大44°，则∠1=________. 67°25. 如图2-59-22,点M,N都在线段AB上，且M分AB为2∶3两部分，N分AB为3∶4两部分，若MN=2 cm，则AB的长为________ cm.7026. 如果∠A和∠B互补，且∠A＞∠B，给出下列四个式子：①90°-∠B；②∠A-90°；③ （∠A+∠B）；④ （∠A-∠B）.其中表示∠B的余角的式子有____________．（填序号）27. 钟表上11点15分时，时针与分针的夹角为__________度. ①②④112.528. 如图2-59-23，已知OM，ON分别是∠BOC和∠AOC的平分线，已知∠AOB=86°.（1）∠MON=________度；（2）当OC在∠AOB内绕点O转动时，∠MON的值________改变．（填“会”或“不会”）43不会29. 如图2-59-24．点O是直线AB上一点，∠AOE是直角，∠FOD=90°，OB平分∠DOC．（1）求与∠DOE所有互为余角的角；（2）求与∠DOE所有互为补角的角；（3）若∠AOF=70°，求∠DOC的度数．解：（1）因为∠AOE=∠FOD=90°，所以∠AOF+∠EOF=90°，∠BOD+∠DOE=90°，∠DOE+∠EOF=90°.因为OB平分∠COD，所以∠BOD=∠BOC.所以与∠DOE互余的角是∠EOF，∠BOD，∠BOC.（2）因为∠AOF+∠BOF=180°，∠AOF=∠DOE，所以∠DOE+∠BOF=180°.又因为∠EOF=∠BOD=∠BOC，所以∠BOF=∠EOC.所以与∠DOE互补的角是∠BOF，∠EOC.（3）因为∠AOF=70°，所以∠DOE=70°.所以∠DOB=20°.因为OB平分∠DOC，所以∠DOC=2∠DOB=40°．30. 如图2-59-25，数轴上的点O和A分别表示0和10，点P是线段OA上一动点，沿O→A→O以每秒2个单位长度的速度往返运动1次，B是线段OA的中点，设点P运动时间为t s（0≤t≤10）．（1）线段BA的长度为________；（2）当t=3时，点P所表示的数是________；56（3）求动点P所表示的数（用含t的代数式表示）；（4）在运动过程中，若OP中点为Q，则QB的长度是否发生变化？若不变，请求出它的值；若变化，请直接用含t的代数式表示QB的长度．解：（3）当0≤t≤5时，动点P所表示的数是2t；当5