

2021-2022学年陕西省西安市雁塔区八年级(上)期中数学试卷 解析版
展开
这是一份2021-2022学年陕西省西安市雁塔区八年级(上)期中数学试卷 解析版,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年陕西省西安市雁塔区八年级(上)期中数学试卷
一、选择题(共10小题,每小题3分,共30分,每小题只有一个选项是符合题意的)
1.(3分)在实数,,﹣,,,3.14,1.010010001…(相邻两个1之间0的个数逐次加1)中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)下列是二元一次方程的是( )
A.3x﹣6=x B.3x=2y C.x﹣=0 D.2x﹣3y=xy
3.(3分)下列各组数为边长的三角形中,是直角三角形的是( )
A.,, B.5,12,13 C.,, D.5,6,7
4.(3分)下列判断正确的是( )
A.正数a的算术平方根是 B.﹣9的算术平方根是3
C.27的立方根是土3 D.=±4
5.(3分)已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
A.﹣3 B.﹣5 C.1或﹣3 D.1或﹣5
6.(3分)在平面直角坐标系中,将直线y=﹣2x向上平移3个单位,平移后的直线经过点(﹣1,m),则m的值为( )
A.﹣1 B.1 C.﹣5 D.5
7.(3分)为迎接2022年北京冬奥会,某班开展了以迎冬奥为主题的体育活动,计划拿出200元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件25元,乙种奖品每件10元,则购买方案有( )
A.2种 B.3种 C.4种 D.5种
8.(3分)已知一次函数y=kx﹣b,y随着x的增大而增大,且kb<0,则它的大致图象是( )
A.
B.
C.
D.
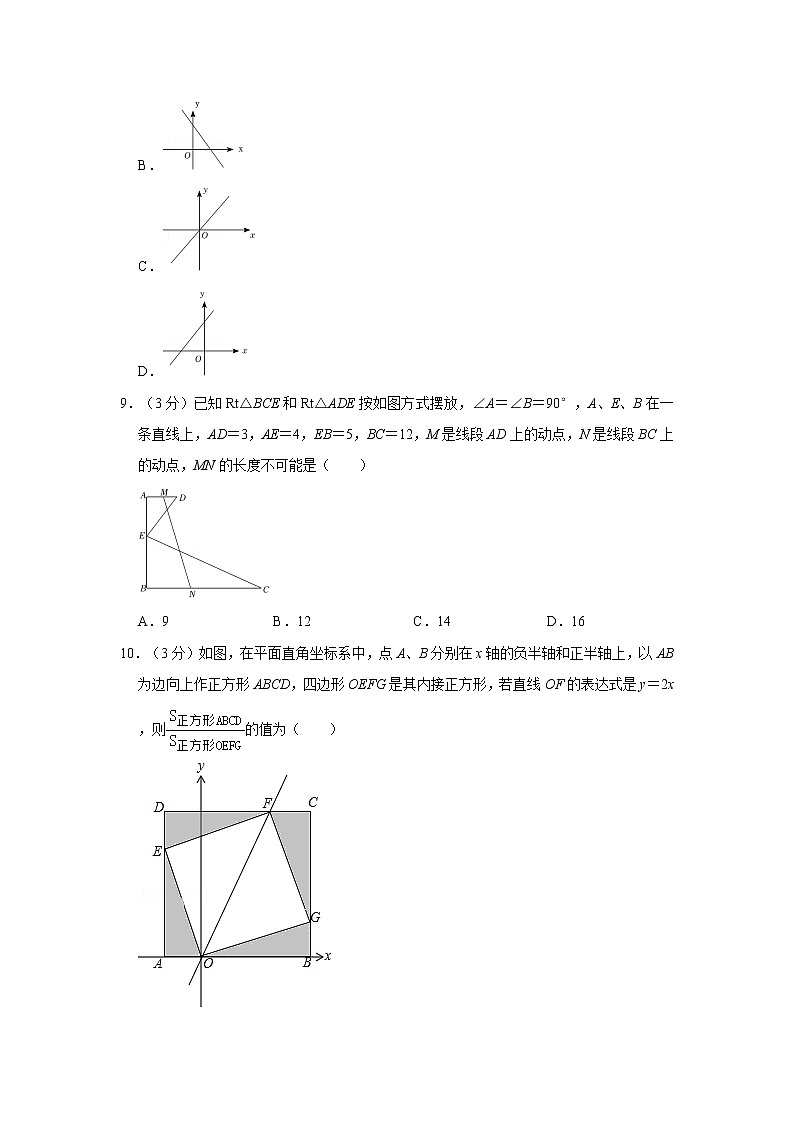
9.(3分)已知Rt△BCE和Rt△ADE按如图方式摆放,∠A=∠B=90°,A、E、B在一条直线上,AD=3,AE=4,EB=5,BC=12,M是线段AD上的动点,N是线段BC上的动点,MN的长度不可能是( )
A.9 B.12 C.14 D.16
10.(3分)如图,在平面直角坐标系中,点A、B分别在x轴的负半轴和正半轴上,以AB为边向上作正方形ABCD,四边形OEFG是其内接正方形,若直线OF的表达式是y=2x,则的值为( )
A. B. C. D.
二、填空题(共6小题,每小题3分,共18分)
11.(3分)比较大小:﹣ ﹣.(填>、=或<)
12.(3分)若关于x,y的方程(k﹣2)x|k|﹣1﹣7y=8是二元一次方程,则k= .
13.(3分)对于非0实数a,b,则点(﹣a2﹣1,)关于x轴的对称点一定在第 象限.
14.(3分)如图,在Rt△ABC中,∠A=90°,AC=2,AB=2,D、E分别是AB和BC上的点,若把△BDE沿DE翻折,B的对应点恰好落在AC的中点处,则BD的长是 .
15.(3分)已知直线y=﹣2x+4与x轴,y轴分别交于A、B两点,M是第一象限内的点,若△MAB是以AB为斜边的等腰直角三角形,则M点的坐标是 .
16.(3分)在Rt△ABC中,∠B=90°,AB=3,BC=4,点E是△ABC内一点,点D是BC的中点,连接DE、AE,且DE=DB,点F是DE的中点,则AE+CF的最小值是 .(提示:连接CE,等腰三角形两腰上的中线相等)
三、解答题(共7小题,共52分.解答题应写出必要的过程)
17.(8分)计算:
(1)|1﹣|+(﹣)﹣1﹣+(﹣π)0;
(2)+9﹣+()2.
18.(8分)解方程组:
(1);
(2).
19.(6分)已知a=2+,b=2﹣,求下列式子的值:
(1)a2﹣3ab+b2;
(2)(a+1)(b+1).
20.(6分)学校校园一角有一块如图所示的三角形空地ABC,其中AB=13米,BC=15米,AC=4米,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,请通过计算估计学校修建这个花园需要投资多少元?
21.(6分)某物流公司的一辆货车A从乙地出发运送货物至甲地,1小时后,这家公司的一辆货车B从甲地出发送货至乙地.货车A、货车B距甲地的距离y(km)与时间x(h)之间的关系如图所示.
(1)求货车B距甲地的距离y与时间x的关系式;
(2)求货车B到乙地后,货车A还需多长时间到达甲地.
22.(8分)如图,在平面直角坐标系中,网格正方形的边长是1,已知A(﹣2,5),B(0,1),C(2,2).
(1)画出△ABC;
(2)求△ABC的面积;
(3)P为x轴上一点,且△PAB的面积等于△ABC的面积,求点P的坐标.
23.(10分)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
2021-2022学年陕西省西安市雁塔区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(共10小题,每小题3分,共30分,每小题只有一个选项是符合题意的)
1.(3分)在实数,,﹣,,,3.14,1.010010001…(相邻两个1之间0的个数逐次加1)中,无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数、有理数的定义即可求解(无理数为无限不循环小数,整数和分数统称有理数).
【解答】解:=2,
在所列实数中,无理数有,﹣,,1.010010001…(相邻两个1之间0的个数逐次加1),共有4个,
故选:D.
2.(3分)下列是二元一次方程的是( )
A.3x﹣6=x B.3x=2y C.x﹣=0 D.2x﹣3y=xy
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【解答】解:A、3x﹣6=x是一元一次方程;
B、3x=2y是二元一次方程;
C、x﹣=0是分式方程;
D、2x﹣3y=xy是二元二次方程
故选:B.
3.(3分)下列各组数为边长的三角形中,是直角三角形的是( )
A.,, B.5,12,13 C.,, D.5,6,7
【分析】利用勾股定理的逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.由此判定即可.
【解答】解:A、因为()2+()2≠()2,所以三条线段不能组成直角三角形,不符合题意;
B、因为52+122=132,所以三条线段能组成直角三角形,符合题意;
C、因为()2+()2≠()2,所以三条线段不能组成直角三角形,不符合题意;
D、因为52+62≠72,所以三条线段不能组成直角三角形,不符合题意.
故选:B.
4.(3分)下列判断正确的是( )
A.正数a的算术平方根是 B.﹣9的算术平方根是3
C.27的立方根是土3 D.=±4
【分析】根据平方根、算术平方根、立方根的定义逐项进行判断即可.
【解答】解:A.正数a的算术平方根是,是正确的,因此选项A符合题意;
B.负数没有平方根,因此选项B不符合题意;
C.27的立方根是3,因此选项C不符合题意;
D.=4,即16的算术平方根是4,因此选项D不符合题意;
故选:A.
5.(3分)已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
A.﹣3 B.﹣5 C.1或﹣3 D.1或﹣5
【分析】根据点A(a+2,4)和B(3,2a+2)到x轴的距离相等,得到4=|2a+2|,即可解答.
【解答】解:∵点A(a+2,4)和B(3,2a+2)到x轴的距离相等,
∴4=|2a+2|,a+2≠3
解得:a=﹣3,
故选:A.
6.(3分)在平面直角坐标系中,将直线y=﹣2x向上平移3个单位,平移后的直线经过点(﹣1,m),则m的值为( )
A.﹣1 B.1 C.﹣5 D.5
【分析】先根据平移规律求出直线y=﹣2x向上平移3个单位的直线解析式,再把点(﹣1,m)代入,即可求出m的值.
【解答】解:将直线y=﹣2x向上平移3个单位,得到直线y=﹣2x+3,
把点(﹣1,m)代入,得m=﹣2×(﹣1)+3=5.
故选:D.
7.(3分)为迎接2022年北京冬奥会,某班开展了以迎冬奥为主题的体育活动,计划拿出200元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件25元,乙种奖品每件10元,则购买方案有( )
A.2种 B.3种 C.4种 D.5种
【分析】设购买x件甲种奖品,y件乙种奖品,根据总价=单价×数量,即可得出关于x,y的二元一次方程,结合x,y均为正整数,即可得出x,y的值,进而可得出共有3种购买方案.
【解答】解:设购买x件甲种奖品,y件乙种奖品,
依题意得:25x+10y=200,
∴x=8﹣y.
又∵x,y均为正整数,
∴或或,
∴共有3种情况.
故选:B.
8.(3分)已知一次函数y=kx﹣b,y随着x的增大而增大,且kb<0,则它的大致图象是( )
A.
B.
C.
D.
【分析】根据一次函数y=kx﹣b,y随着x的增大而增大,且kb<0,可以得到k、b的正负情况,然后根据一次函数的性质,即可得到该函数的图象经过哪几个象限,从而可以解答本题.
【解答】解:∵一次函数y=kx﹣b,y随着x的增大而增大,且kb<0,
∴k>0,b<0,
∴﹣b>0,
∴该函数图象经过第一、二、三象限,
故选:D.
9.(3分)已知Rt△BCE和Rt△ADE按如图方式摆放,∠A=∠B=90°,A、E、B在一条直线上,AD=3,AE=4,EB=5,BC=12,M是线段AD上的动点,N是线段BC上的动点,MN的长度不可能是( )
A.9 B.12 C.14 D.16
【分析】根据已知条件易求AB=9,AD∥BC,再确定MN的最大值及最小值可求出MN的取值范围,进而可求解.
【解答】解:∵AE=4,EB=5,
∴AB=AE+EB=4+5=9,
∵∠DAE=∠B=90°,
∴∠DAE+∠B=180°,
∴AD∥BC,
当M点与A点重合,N点与C点重合时,如图,
∵∠B=90°,BC=12,
∴MN=;
当M点与A点重合,N点与B点重合时,如图,
MN=AB=9,
∴9≤MN≤15,
∴MN的长度不可能是16,
故选:D.
10.(3分)如图,在平面直角坐标系中,点A、B分别在x轴的负半轴和正半轴上,以AB为边向上作正方形ABCD,四边形OEFG是其内接正方形,若直线OF的表达式是y=2x,则的值为( )
A. B. C. D.
【分析】过F作FH⊥AB于H,根据矩形的性质得到FH=AD,设F(m,2m),求得AD=FH=2m,OH=m,根据勾股定理得到OF==m,根据正方形的面积公式即可得到答案.
【解答】解:过F作FH⊥AB于H,
则四边形AHFD是矩形,
∴FH=AD,
∵直线OF的表达式是y=2x,
∴设F(m,2m),
∴AD=FH=2m,OH=m,
∴OF==m,
∵四边形OGFE是正方形,
∴OG=OF=m,
∴===,
故选:B.
二、填空题(共6小题,每小题3分,共18分)
11.(3分)比较大小:﹣ > ﹣.(填>、=或<)
【分析】根据分数的意义、平方根的定义先进行估算,再进行比较即可得出答案.
【解答】解:∵()2=,()2=10,
∵<10,
∴﹣>﹣.
故答案为:>.
12.(3分)若关于x,y的方程(k﹣2)x|k|﹣1﹣7y=8是二元一次方程,则k= ﹣2 .
【分析】二元一次方程满足的条件:含有2个未知数,含未知数的项的次数是1的整式方程,据此解答即可.
【解答】解:根据题意得:
,
解得k=﹣2.
故答案为:﹣2.
13.(3分)对于非0实数a,b,则点(﹣a2﹣1,)关于x轴的对称点一定在第 第三 象限.
【分析】根据a,b是非0实数,得﹣a2﹣1<0,>0,横坐标为负,纵坐标为正,此点在第二象限,关于x轴的对称点,横坐标为负,纵坐标为负,因此在第三象限.
【解答】解:∵a,b是非0实数,
∴﹣a2﹣1<0,>0,
∴此点在第二象限,
∴此点关于x轴的对称点一定在第三象限,
故答案为:第三.
14.(3分)如图,在Rt△ABC中,∠A=90°,AC=2,AB=2,D、E分别是AB和BC上的点,若把△BDE沿DE翻折,B的对应点恰好落在AC的中点处,则BD的长是 .
【分析】由AC=2,B'是AC中点,得AB'=AC=,设BD=x,则AD=AB﹣BD=2﹣x,在Rt△AB'D中,用勾股定理可得(2﹣x)2+()2=x2,即可解得BD=.
【解答】解:∵AC=2,B'是AC中点,
∴AB'=AC=,
设BD=x,则AD=AB﹣BD=2﹣x,
∵把△BDE沿DE翻折,B的对应点恰好落在AC的中点处,
∴B'D=BD=x,
在Rt△AB'D中,AD2+AB'2=B'D2,
∴(2﹣x)2+()2=x2,
解得x=,
∴BD=,
故答案为:.
15.(3分)已知直线y=﹣2x+4与x轴,y轴分别交于A、B两点,M是第一象限内的点,若△MAB是以AB为斜边的等腰直角三角形,则M点的坐标是 (3,3) .
【分析】设M点的坐标是(x,y),由直线y=﹣2x+4与x轴,y轴分别交于A、B两点得出A、B两点的坐标,根据MA=MB,MA2+MB2=AB2得列方程组求解即可.
【解答】解:设M点的坐标是(x,y),
∵直线y=﹣2x+4与x轴,y轴分别交于A、B两点,
∴A(2,0),B(0,4),
∴MA=,MB=,
∵△MAB是以AB为斜边的等腰直角三角形,
∴MA=MB,MA2+MB2=AB2,
∴=且(x﹣2)2+y2+x2+(4﹣y)2=22+42,
解得:或(不合题意,舍去),
∴M(3,3),
故答案为:(3,3).
16.(3分)在Rt△ABC中,∠B=90°,AB=3,BC=4,点E是△ABC内一点,点D是BC的中点,连接DE、AE,且DE=DB,点F是DE的中点,则AE+CF的最小值是 3 .(提示:连接CE,等腰三角形两腰上的中线相等)
【分析】取CD的中点G,连接CE,EG,AG,通过证明△EGD≌△CFD得到CF=EG;根据两点之间线段最短可知:AE+CF=AE+EG≥AG,于是得到当A,E,G三点共线时,AE+CF有最小值AG,利用勾股定理即可求得AG的长.
【解答】解:取CD的中点G,连接CE,EG,AG,如图,
∵点D是BC的中点,
∴BD=CD.
∵DE=DB,
∴DE=DC.
∵点F是DE的中点,点G是DC的中点,
∴DF=DE,DG=DC.
∴DF=DG,
在△EGD和△CFD中,
,
∴△EGD≌△CFD(SAS).
∴EG=CF.
∴AE+CF=AE+EG.
∵两点之间线段最短,
∴AE+EG≥AG,
∴当A,E,G三点共线时,AE+EG有最小值AG,
∴AE+CF有最小值AG,
∵BC=4,
∴BD=DC=2,
∴DG=GC=1.
∴BG=BD+DG=3.
∴AG===3.
答:AE+CF的最小值是3.
故答案为:3.
三、解答题(共7小题,共52分.解答题应写出必要的过程)
17.(8分)计算:
(1)|1﹣|+(﹣)﹣1﹣+(﹣π)0;
(2)+9﹣+()2.
【分析】(1)利用绝对值、负整数指数幂和零指数幂的意义计算;
(2)先把各二次根式化简,然后合并即可.
【解答】解:(1)原式=﹣1﹣3﹣2+1
=﹣3﹣;
(2)原式=5+9×﹣×2+5
=5+﹣+5
=5+5.
18.(8分)解方程组:
(1);
(2).
【分析】(1)利用加减消元法求解即可;
(2)方程组整理后,利用加减消元法求解即可.
【解答】解:(1),
①+②×2,得11x=﹣11,
解得x=﹣1,
把x=﹣1代入②,得y=2,
故方程组的解为;
(2)方程组整理,得,
②×2﹣①,得5x=10,
解得x=2,
把x=2代入②,得6﹣2y=6,
解得y=0,
故方程组的解为.
19.(6分)已知a=2+,b=2﹣,求下列式子的值:
(1)a2﹣3ab+b2;
(2)(a+1)(b+1).
【分析】(1)利用完全平方公式将原式进行变形,然后代入求值;
(2)将a和b的值代入原式,然后利用平方差公式进行计算.
【解答】解:(1)原式=(a﹣b)2﹣ab,
当a=2+,b=2﹣时,
原式=[2+﹣(2﹣)]2﹣(2+)(2﹣)
=(2+﹣2+)2﹣(4﹣6)
=(2)2﹣(﹣2)
=24+2
=26;
(2)当a=2+,b=2﹣时,
原式=(2++1)(2﹣+1)
=(3+)(3﹣)
=9﹣6
=3.
20.(6分)学校校园一角有一块如图所示的三角形空地ABC,其中AB=13米,BC=15米,AC=4米,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,请通过计算估计学校修建这个花园需要投资多少元?
【分析】过点A作AD⊥BC于点D,设BD=x米,则CD=(15﹣x)米,再根据勾股定理求出x的值,进而可得出AD的长,然后由三角形的面积公式即可求解.
【解答】解:过点A作AD⊥BC于点D,如图所示:
设BD=x米,则CD=(15﹣x)米,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,即132﹣x2=42﹣(15﹣x)2,
解得:x=12.6(米),
∴AD2=AB2﹣BD2=132﹣12.62=10.24(平方米),
∴AD=3.2(米),
∴学校修建这个花园的费用为:×15×3.2×60=1440(元),
答:学校修建这个花园需要投资1440元.
21.(6分)某物流公司的一辆货车A从乙地出发运送货物至甲地,1小时后,这家公司的一辆货车B从甲地出发送货至乙地.货车A、货车B距甲地的距离y(km)与时间x(h)之间的关系如图所示.
(1)求货车B距甲地的距离y与时间x的关系式;
(2)求货车B到乙地后,货车A还需多长时间到达甲地.
【分析】(1)设货车B距甲地的距离y与时间x的关系式为y=kx+b,把(1,0),(5,240)代入求解即可;
(2)把x=3代入(1)的结论求出货车B行驶2小时时的路程,进而求出货车A的速度,然后根据“时间=路程÷速度”列式计算即可.
【解答】解:(1)设货车B距甲地的距离y与时间x的关系式为y=kx+b,
根据题意得:
,
解得,
∴货车B距甲地的距离y与时间x的关系式为y=60x﹣60(1≤x≤5);
(2)当x=3时,y=60×3﹣60=120,
故货车A的速度为:(240﹣120)÷3=40(km/h),
货车A到达甲地所需时间为:240÷40=6(小时),
6﹣5=1(小时),
答:货车B到乙地后,货车A还需1小时到达甲地.
22.(8分)如图,在平面直角坐标系中,网格正方形的边长是1,已知A(﹣2,5),B(0,1),C(2,2).
(1)画出△ABC;
(2)求△ABC的面积;
(3)P为x轴上一点,且△PAB的面积等于△ABC的面积,求点P的坐标.
【分析】(1)分别作出A,B,C三点即可;
(2)利用分割法求三角形的面积即可.
(3)结合(2)根据网格即可在x轴上找到一点P,且△PAB的面积等于△ABC的面积.
【解答】解:(1)如图,△ABC即为所求;
(2)△ABC的面积=4×4﹣2×4﹣1×2﹣3×4=16﹣4﹣1﹣6=5;
(3)如图,点P即为所求.
设点P(x,0),
∵△PAB的面积等于△ABC的面积,
∴5×|x+2|﹣1×|x|﹣2×(1+5)=5,
解得x=3或x=﹣2,
∴P(3,0)或(﹣2,0).
23.(10分)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 (1,7) .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
【分析】(1)通过解方程组即可确定点C的坐标;
(2)设点M的坐标为(a,a+6),由MN∥x轴可得点N的坐标是(,a+6),根据MN=6列方程即可求得答案;
(3)根据点M的坐标可得MC、NC、MN的值,由直线y=x+6交x轴于点A,交y轴于点B求出OB,可得OB=MN,分两种情况:当BP=NC,OP=MC时;当BP=MC,OP=NC时,根据全等三角形的性质即可求解.
【解答】解:(1)解方程组,得,
所以点C的坐标为(1,7),
故答案为:(1,7);
(2)∵M是直线AB上一点,
设点M的坐标为(a,a+6),
∵MN∥x轴,点N是直线y=﹣2x+9上一点,
∴a+6=﹣2x+9,解得x=,
∴点N的坐标是(,a+6),
∵MN=6,
∴|﹣a|=6,解得:a=5或﹣3,
∴点M的坐标为(5,11)或(﹣3,3);
(3)存在,
①点M的坐标为(﹣3,3)时,点N的坐标为(3,3),
∴MN=6,MC==,NC==,
设点P的坐标为(x,y),
∵直线y=x+6交x轴于点A,交y轴于点B,
∴B(0,6),OB=6=MN,
当BP=NC,OP=MC时;
,解得:或,
∴点P的坐标为(4,4)或(﹣4,4),
当BP=MC,OP=NC时,
,解得:或,
∴点P的坐标为(4,2)或(﹣4,2),
②点M的坐标为(5,11)时,点N的坐标为(﹣1,11),
∴MN=6,MC==,NC==,
此时△MNC与①中的△MNC三边都对应相等,所以此时情况与①相同.
综上,点P的坐标为(4,4)或(﹣4,4)或(4,2)或(﹣4,2).
相关试卷
这是一份2022-2023学年陕西省西安市雁塔区高新一中八年级(上)期中数学试卷(含答案解析),共17页。试卷主要包含了12131415C,【答案】D,【答案】B,【答案】C,【答案】A等内容,欢迎下载使用。
这是一份2022-2023学年陕西省西安市雁塔区高新一中七年级(上)期中数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021-2022学年陕西省西安市雁塔区高新一中八年级(下)期中数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








