



矩形、菱形、正方形数学专题课件 2021年中考一轮复习(人教版)
展开
这是一份矩形、菱形、正方形数学专题课件 2021年中考一轮复习(人教版),共50页。PPT课件主要包含了三个内角,垂直且互相平分,一组对角,互相垂直,相等且互相垂直,互相垂直平分等内容,欢迎下载使用。
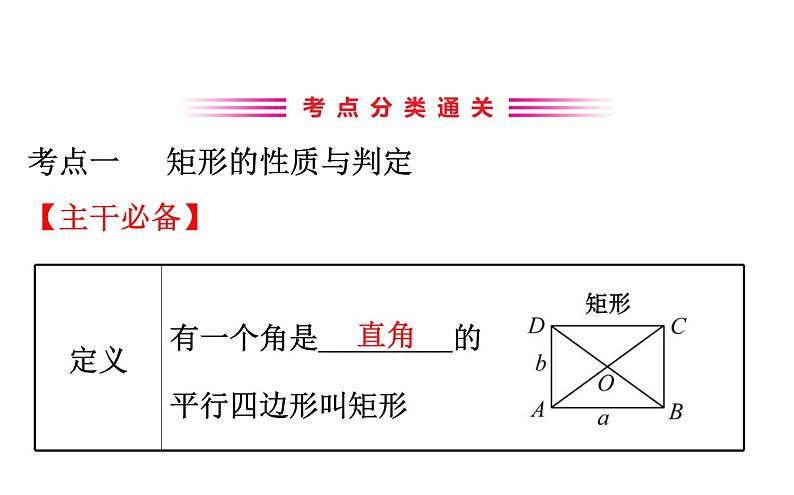
考点一 矩形的性质与判定【主干必备】
【微点警示】 1.矩形的一条对角线将矩形分成两个全等的直角三角形.2.矩形的两条对角线将矩形分成面积相等的四个小等腰三角形.
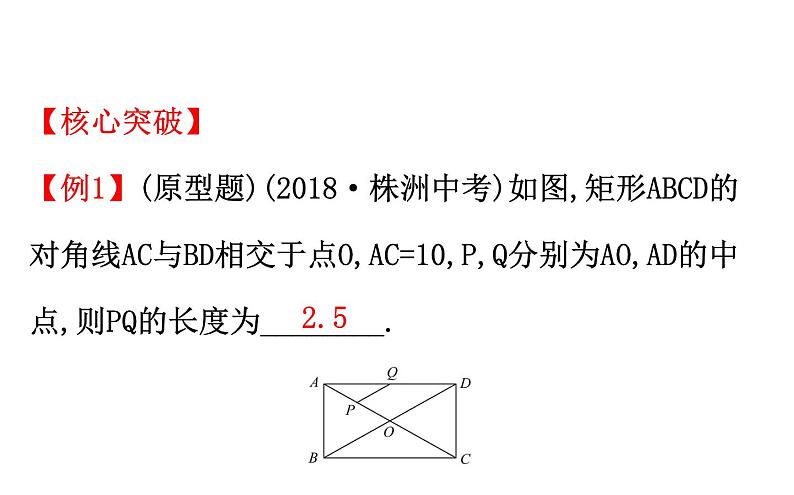
【核心突破】【例1】(原型题)(2018·株洲中考)如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为________.
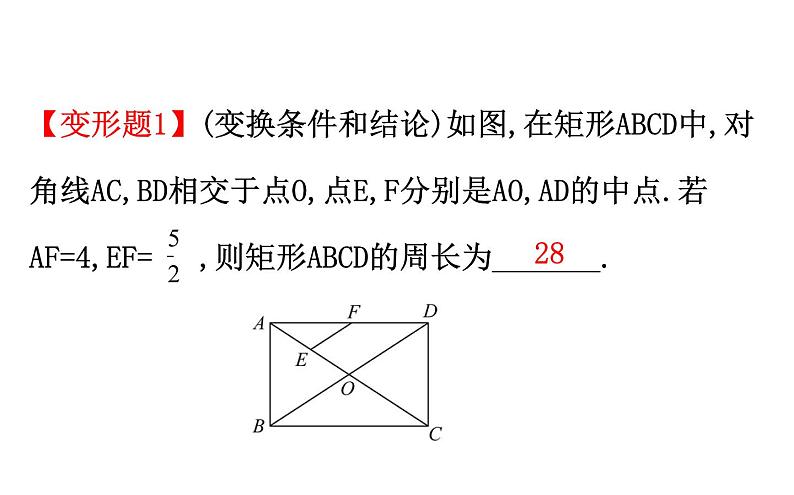
【变形题1】(变换条件和结论)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点.若AF=4,EF= ,则矩形ABCD的周长为_______.
【变形题2】(中位线变为动线)如图,矩形ABCD中,BC=6,AB=3,R在CD边上,且CR=1,P为BC上一动点,E,F分别是AP,RP的中点,当P从B向C移动时,线段EF的长度为____.
【明·技法】矩形的判定思路(1)①若给出的图形是一般的四边形.思路一:证明有三个角都是直角.
思路二:先证明为平行四边形,再证明有一个角是直角或证明其对角线相等.②若给出的四边形是平行四边形,则直接证明有一个角是直角或证明对角线相等.
(2)矩形除了具有平行四边形所有的性质以外,还在角和对角线上具有自身的特性:四个角都是直角,对角线相等,矩形的一条对角线将矩形分成两个直角三角形,矩形的两条对角线将矩形分成四个等腰三角形.
【题组过关】1.(2019·泉州模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠AOD=120°,AC=6,则图中长度为3的线段有( )A.2条 B.4条 C.5条 D.6条
2.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作BD的垂线,垂足为点E.已知∠EAD=3∠BAE,则∠EAO的度数为( )A.22.5°B.67.5°C.45°D.60°
3.(2019·新乡卫辉模拟)如图,在△ABC中,AB=6, AC=8,BC=10.P为BC上一动点,PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为________.
4.如图,四边形ABEF中,AF∥BE,点D是BE的中点,AD与BF交于点C,AC=CD.(1)求证:AF=DE.(2)如果AB=AE,试判断四边形ADEF的形状.并证明你的结论.略
考点二 菱形的性质与判定【主干必备】
【微点警示】 1.菱形的一条对角线把菱形分成两个全等的等腰三角形.2.菱形的两条对角线把菱形分成四个全等的直角三角形.
【核心突破】【例2】(2019·兰州中考)如图,AC=8,分别以A,C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D.依次连接A,B,C,D,连接BD交AC于点O.
(1)判断四边形ABCD的形状并说明理由.(2)求BD的长.
【自主解答】(1)四边形ABCD为菱形.由作法得AB=AD=CB=CD=5,所以四边形ABCD为菱形.
(2)∵四边形ABCD为菱形,∴OA=OC=4,OB=OD,AC⊥BD,在Rt△AOB中,OB= =3,∴BD=2OB=6.
【明·技法】菱形的性质与判定1.性质:(1)菱形的对边平行,对角相等,四边相等,常用等量代换来转换为其他的边和角求解问题,(2)利用对角线垂直借助勾股定理求线段的长.
2.判定:(1)先证明四边形是一个平行四边形,再证明一组邻边相等或证明对角线互相垂直.(2)证明四条边相等或对角线互相垂直且平分.
【题组过关】1.(2019·成都锦江区模拟)如图,在菱形ABCD中, ∠A=130°,连接BD,∠DBC等于( )A.25°B.35°C.50°D.65°
2.(2019·三明建宁县期中)如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )A.18 B.18 C.9 D.6
3.如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.且AD交EF于点O,则∠AOF=_______度.
4.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为点F,连接CD,BE.
(1)求证:CE=AD.(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
【解析】(1)∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD.
(2)四边形BECD是菱形,理由如下:∵D为AB的中点,∴AD=BD,∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形,∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形.
考点三 正方形的性质与判定【主干必备】1.正方形的性质与判定:
2.平行四边形、矩形、菱形、正方形的关系:
【核心突破】【例3】(2019·甘肃中考)如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
(1)证明:△ADG≌△DCE.(2)连接BF,证明:AB=FB.
【自主解答】(1)∵四边形ABCD是正方形,∴∠ADG=∠C=90°,AD=DC,又∵AG⊥DE,∴∠DAG+∠ADF=90°=∠CDE+∠ADF,∴∠DAG=∠CDE,∴△ADG≌△DCE(ASA).
(2)如图所示,延长DE交AB的延长线于H,∵E是BC的中点,∴BE=CE,又∵∠C=∠HBE=90°,∠DEC=∠HEB,∴△DCE≌△HBE(ASA),
∴BH=DC=AB,即B是AH的中点,又∵∠AFH=90°,∴在Rt△AFH中,BF= AH=AB.
【明·技法】正方形的性质及判定1.正方形的性质: (1)正方形的四条边都相等,四个角都是直角.(2)正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角.
(3)正方形具有四边形、平行四边形、矩形、菱形的一切性质.
2.正方形的四个判定方法:(1)有一个角是直角的菱形是正方形.(2)有一组邻边相等的矩形是正方形.(3)对角线相等的菱形是正方形.(4)对角线互相垂直的矩形是正方形.
【题组过关】1.(2019·宁德模拟)如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的大小是( )A.67.5° B.22.5° C.30° D.45°
2.(2019·苏州太仓期末)如图,等边△ABC与正方形DEFG重叠,其中D,E两点分别在AB,BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为( )A.1 B.2 C.2 D.4
3.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,若∠CBF=20°,则∠DEF=_______度.
相关课件
这是一份2024河南中考数学一轮知识点训练复习专题 矩形、菱形和正方形 (课件),共33页。PPT课件主要包含了第2题,第3题,第6题,第7题,第10题,第11题,第14题,第15题,第16题,第17题等内容,欢迎下载使用。
这是一份2024河南中考数学一轮知识点复习专题 矩形、菱形和正方形 课件,共52页。PPT课件主要包含了矩形的判定,菱形的判定,正方形的判定,考点3中点四边形,常见结论,基础题过考点,考点1→,考点2→,平行四边形,正方形等内容,欢迎下载使用。
这是一份中考数学一轮总复习: 矩形、菱形、正方形 课件,共32页。PPT课件主要包含了矩形常考点,菱形常考点,正方形常考点,中点四边形,°或80°等内容,欢迎下载使用。









