初中数学1 认识三角形精品课件ppt

这是一份初中数学1 认识三角形精品课件ppt，文件包含北师大版七年级数学下册412三角形的边pptx、北师大版七年级数学下册412三角形的边docx等2份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
1.掌握三角形按边分类的方法，能够判定三角形是否为特殊三角形;2.探索并掌握三角形三边之间的关系，运用三角形三边关系解决有关问题．3.掌握三角形三边的不等关系，并能运用三角形三边的不等关系解决实际问题。
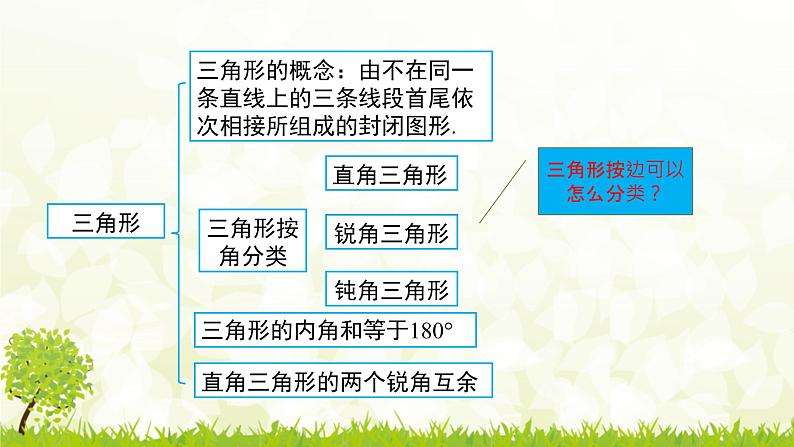
三角形的概念：由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
三角形的内角和等于180°
直角三角形的两个锐角互余
三角形按边可以怎么分类？
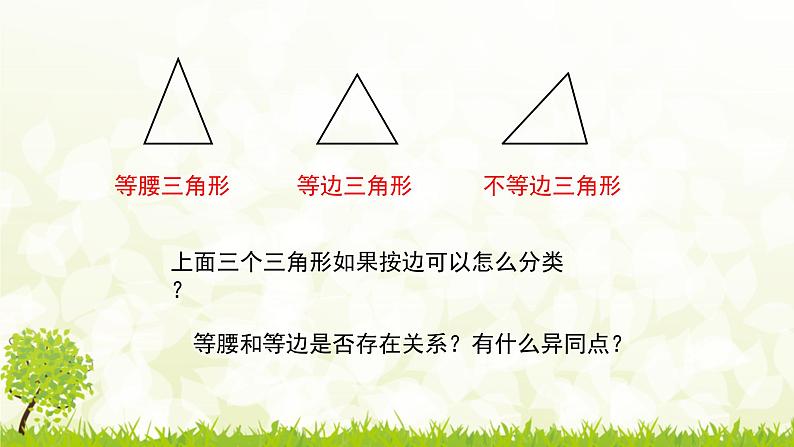
上面三个三角形如果按边可以怎么分类？
等腰和等边是否存在关系？有什么异同点？
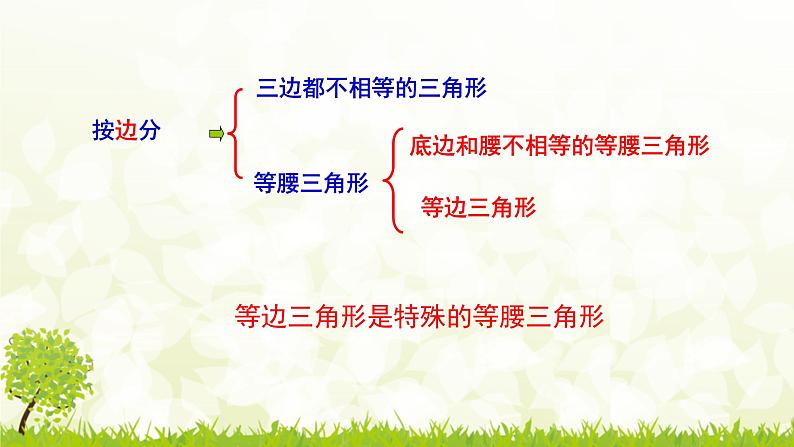
等边三角形是特殊的等腰三角形
单独思考： 1.在同一个三角形中,任意两边之和与第三边有什么大小关系? 三角形任意两边的和大于第三边2.在同一个三角形中,任意两边之差与第三边有什么大小关系? 三角形两边的差小于第三边.
例1 有两根长度分别为4cm和6cm的木棒，用长度为2cm的木棒与它们能摆成三角形吗？为什么？长度为11cm的木棒呢？
判断三条线段是否可以组成三角形，只需说明两条较短线段之和大于第三条线段即可
解：取长度为2cm的木棒时，由于2+4=6=8，出现了两边之和等于第三边的情况，所以它们不能摆成三角形.取长度为13cm的木棒时，由于4+6=10＜13，出现了两边之和小于第三边的情况，所以它们也不能摆成三角形.
三角形两边的和大于第三边.三角形两边的差小于第三边.
注意：两边的和要大于第三边，相等也是不允许的，同理，两边之差必须小于第三边，也不能相等。
下列长度的3根小木棒不能构成三角形的是（ 
） A.2 cm,3 cm,4 cm
 B.1 cm,2 cm,3 cm C.3cm,4 cm,5cm D.4 cm,5 cm,6 cm
若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（ ）
用一根长为10 cm的绳子围成一个三角形，若所围成的三角形中一边的长为2cm，且另外两边长的值均为整数，则这样的围法有（ ）A.1种B.2种C.3种D.4种
等腰三角形的周长为16，其一边长为6，求另两边的长.
有一条长为21 cm的细绳围成的一个等腰三角形.(1)如果腰长是底边长的3倍，那么底边长是多少?(2）能围成一边长为5cm的等腰三角形吗?说明理由.
已知a，b，c是△ABC的三边长，化简|a+b-cl-|b-a-c|的值是（ ）A.-2cB2b-2cC.2a-2cD.2a-2b
小颖要制作一个三角形木架，现有两根长度为 8cm和5cm的木棒，如果要求第三根木棒的长度是偶数，小颖有几种选法？第三根的长度可以是多少？
∵x为偶数，∴小颖有5种选法.
第三根木棒的长度可以是4cm，6cm，8cm，10cm，12cm.
解：设第三根木棒长为xcm，有8-5＜x＜8+5，
等腰三角形（包括等边三角形）
任意两边之和大于第三边
任意两边之差小于第三边