2022年中考复习基础必刷40题专题41尺规作图

这是一份2022年中考复习基础必刷40题专题41尺规作图，共38页。

1. 某同学的作业如下框，其中※处填的依据是（ ）
A.两直线平行，内错角相等
B.内错角相等，两直线平行
C.两直线平行，同位角相等
D.两直线平行，同旁内角互补

2. 如图，在Rt△ABC中，∠ACB=90∘，BC>AC，按以下步骤作图：
(1)分别以点A，B为圆心，以大于12AB的长为半径作弧，两弧相交于M，N两点（点M在AB的上方）；
(2)作直线MN交AB于点O，交BC于点D；
(3)用圆规在射线OM上截取OE=OD．连接AD，AE，BE，过点O作OF⊥AC．垂足为F，交AD于点G．
下列结论：
①CD=2GF；
②BD2−CD2=AC2；
③S△BOE=2S△AOG；
④若AC=6，OF+OA=9，则四边形ADBE的周长为25．
其中正确的结论有( )

A.1个B.2个C.3个D.4个

3. 如图，在△ABC中，BA=BC，∠B=80∘，观察图中尺规作图的痕迹，则∠DCE的度数为( )

A.60∘B.65∘C.70∘D.75∘

4. 如图，在Rt△ABC中，∠BAC=90∘，以点A为圆心，以AB长为半径作弧交BC于点D，再分别以点B，D为圆心，以大于12BD的长为半径作弧，两弧交于点P，作射线AP交BC于点E，若AB=3，AC=4，则CD=( )

A.125B.95C.85D.75

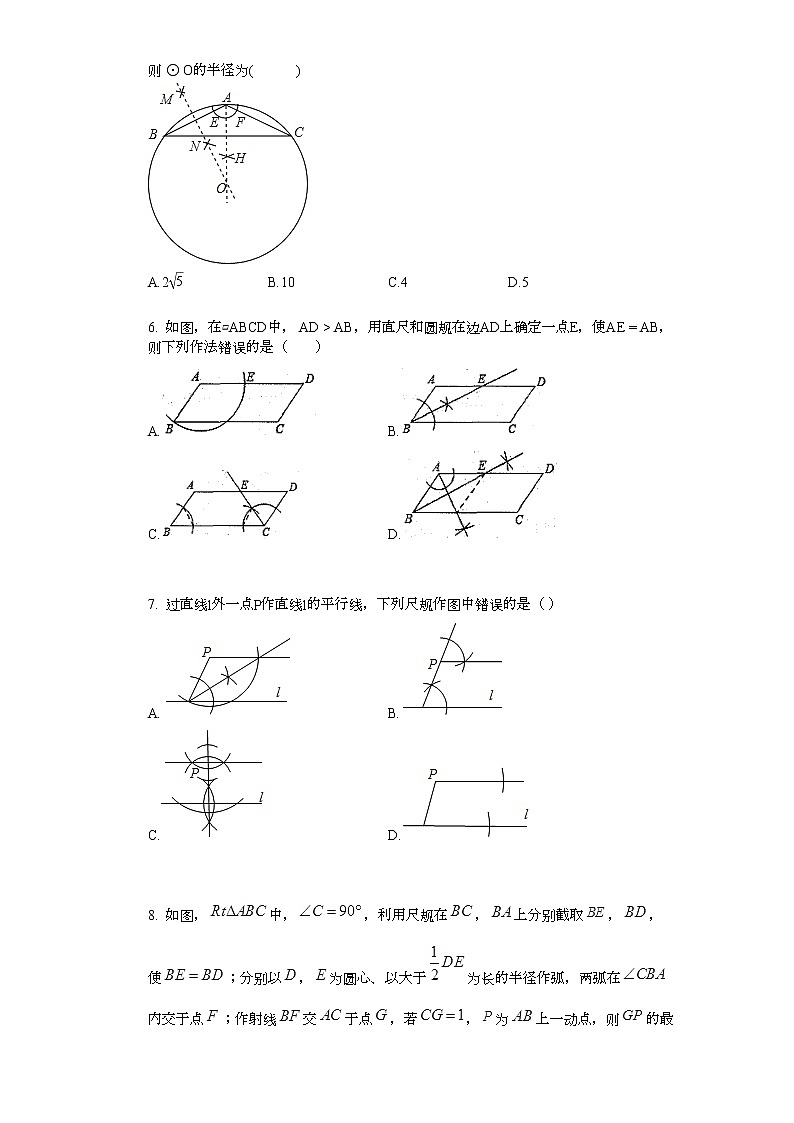
5. 如图，在等腰△ABC中，AB=AC=25，BC=8，按下列步骤作图：
①以点A为圆心，适当的长度为半径作弧，分别交AB，AC于点E，F，再分别以点E，F为圆心，大于12EF的长为半径作弧相交于点H，作射线AH；
②分别以点A，B为圆心，大于12AB的长为半径作弧相交于点M，N，作直线MN，交射线AH于点O；
③以点O为圆心，线段OA长为半径作圆．
则⊙O的半径为( )

A.25B.10C.4D.5

6. 如图，在▱ABCD中， AD>AB，用直尺和圆规在边AD上确定一点E，使AE=AB，则下列作法错误的是（ ）
A.B.
C.D.

7. 过直线l外一点P作直线l的平行线，下列尺规作图中错误的是（ ）
A.B.
C.D.

8. 如图，中，，利用尺规在，上分别截取，，使；分别以，为圆心、以大于为长的半径作弧，两弧在内交于点；作射线交于点，若，为上一动点，则的最小值为( )

A.无法确定B.C.1D.2

9. 如图，△ABC中，ACA.B.
C.D.

10. 如图，点C在∠AOB的边OA上，用尺规作出了CP // OB，作图痕迹中，FG是（ ）

A.以点C为圆心、OD的长为半径的弧
B.以点C为圆心、DM的长为半径的弧
C.以点E为圆心、DM的长为半径的弧
D.以点E为圆心、OD的长为半径的弧

11. 如图，分别以线段AB的两个端点为圆心，大于AB的一半的长为半径画弧，两弧分别交于C，D两点，连接AC，BC，AD，BD，则四边形ADBC一定是（ ）

A.正方形B.矩形C.梯形D.菱形

12. 如图，在中，，以点为圆心，适当长为半径画弧，分别交于点，再分别以点为圆心，大于为半径画弧，两弧交于点，作射线交边于点，则的面积是（ ）

A.B.C.D.

13. 如图，在△ABC中，∠ACB为钝角．用直尺和圆规在边AB上确定一点D．使∠ADC＝2∠B，则符合要求的作图痕迹是（ ）
A.B.
C.D.

14. 如图，点A在双曲线y=kx(x>0)上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于12OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F(0, 2)，连接A
C.435A.2B.3225D.25+25

15. 如图是用直尺和一个等腰直角三角尺画平行线的示意图，图中∠α的度数为（ ）

A.45∘B.60∘C.90∘D.135∘

16. 如图，锐角三角形ABC中，BC>AB>AC，甲、乙两人想找一点P，使得∠BPC与∠A互补，其作法分别如下：
（甲）以A为圆心，AC长为半径画弧交AB于P点，则P即为所求；
（乙）作过B点且与AB垂直的直线l，作过C点且与AC垂直的直线，交l于P点，则P即为所求
对于甲、乙两人的作法，下列叙述何者正确？（ ）

A.两人皆正确B.两人皆错误
C.甲正确，乙错误D.甲错误，乙正确

17. 如图，在中，用直尺和圆规作的平分线，若，则的长是（）

A.B.C.D.

18. 如图，矩形ABCD中，AD＝3AB，O为AD中点，AD是半圆．甲、乙两人想在AD上取一点P，使得△PBC的面积等于矩形ABCD的面积其作法如下：
（甲） 延长BO交AD于P点，则P即为所求；
（乙） 以A为圆心，AB长为半径画弧，交AD于P点，则P即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）

A.两人皆正确B.两人皆错误
C.甲正确，乙错误D.甲错误，乙正确

19. 如图，P为圆O外一点，OP交圆O于A点，且OA＝2AP．甲、乙两人想作一条通过P点且与圆O相切的直线，其作法如下：
（甲）以P为圆心，OP长为半径画弧，交圆O于B点，则直线PB即为所求；
（乙）作OP的中垂线，交圆O于B点，则直线PB即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）

A.两人皆正确B.两人皆错误
C.甲正确，乙错误D.甲错误，乙正确

20. 如图，锐角三角形ABC中，BC>AB>AC，小靖依下列方法作图：
(1)作∠A的角平分线交BC于D点．
(2)作AD的中垂线交AC于E点．
(3)连接DE．
根据他画的图形，判断下列关系何者正确？（ ）
A.DE⊥ACB.DE // ABC.CD=DED.CD=BD

21. 如图，在Rt△ABC中，∠C=90∘，AC=BC，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交 AC，AB于点M，N；②分别以M，N为圆心，以大于12MN的长为半径作弧，两弧在∠BAC内交于点O；③作射线AO，交BC于点D．若点D到AB的距离为1，则BC的长为________．


22. 如图，已知边长为2的等边三角形ABC中，分别以点A，C为圆心，m为半径作弧，两弧交于点D，连结BD．若BD的长为23，则m的值为________．


23. 如图，已知∠MON是一个锐角，以点O为圆心，任意长为半径画弧，分别交OM、ON于点A、B，再分别以点A、B为圆心，大于12AB长为半径画弧，两弧交于点C，画射线OC．过点A作AD // ON，交射线OC于点D，过点D作DE⊥OC，交ON于点E．设OA=10，DE=12，则sin∠MON=________．


24. 如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，C均落在格点上，点B在网格线上，且AB = 53．

(1)线段AC的长等于________；

(2)以BC为直径的半圆与边AC相交于点D，若P，Q分别为边AC，BC上的动点，当BP+PQ取得最小值时，请用无刻度的直尺，在如图所示的网格中，画出点P，Q，并简要说明点P,Q的位置是如何找到的（不要求证明）________.

25. 如图，在x轴，y轴上分别截取OA、OB，使OA=OB，再分别以点A、B为圆心，以大于12AB长为半径画弧，两弧交于点P．若点P的坐标为(a, 2a−3)，则a的值为________．


26. 如图，在菱形ABCD中，∠A=30∘，取大于12AB的长为半径，分别以点A，B为圆心作弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD．则∠EBD的度数为________．


27. 【算一算】
如图①，点A、B、C在数轴上，B为AC的中点，点A表示−3，点B表示1，则点C表示的数为________，AC长等于________；
【找一找】
如图②，点M、N、P、Q中的一点是数轴的原点，点A、B分别表示实数22−1、22+1，Q是AB的中点，则点________是这个数轴的原点；
【画一画】
如图③，点A、B分别表示实数c−n、c+n，在这个数轴上作出表示实数n的点E（要求：尺规作图，不写作法，保留作图痕迹）；
【用一用】
学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测a个学生．凌老师提出了这样的问题：假设现在校门口有m个学生，每分钟又有b个学生到达校门口．如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校．在这些条件下，a、m、b会有怎样的数量关系呢？
爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数m+4b记作+(m+4b)，用点A表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数8a记作−8a，用点B表示．
①用圆规在小华画的数轴上分别画出表示+(m+2b)、−12a的点F、G，并写出+(m+2b)的实际意义；
②写出a、m的数量关系：________．


28. 如图，在中，，，垂直平分，垂足为Q，交于点P．按以下步骤作图：①以点A为圆心，以适当的长为半径作弧，分别交边于点D，E；②分别以点D，E为圆心，以大于的长为半径作弧，两弧相交于点F；⑤作射线．若与的夹角为，则________​∘．

29. 如图，在△ABC中，∠C＝84∘，分别以点A、B为圆心，以大于AB的长为半径画弧，两弧分别交于点M、N，作直线MN交AC点D；以点B为圆心，适当长为半径画弧，分别交BA、BC于点E、F，再分别以点E、F为圆心，大于EF的长为半径画弧，两弧交于点P，作射线BP，此时射线BP恰好经过点D，则∠A＝________度．


30. 如图，▱ABCD的对角线AC与BD相交于点O，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交AO，AB于点M，N；②以点O为圆心，以AM长为半径作弧，交OC于点M′；③以点M′为圆心，以MN长为半径作弧，在∠COB内部交前面的弧于点N′；④过点N′作射线ON′交BC于点E．若AB=8，则线段OE的长为________．


31. 如图，在每个小正方形的边长为1的网格中，△ABC的顶点A在格点上，B是小正方形边的中点，∠ABC=50∘，∠BAC=30∘，经过点A，B的圆的圆心在边AC上．

(1)线段AB的长等于________；

(2)请用无刻度的直尺，在如图所示的网格中，画出一个点P，使其满足∠PAC=∠PBC=∠PCB，并简要说明点P的位置是如何找到的（不要求证明）.

32. 【阅读理解】
用10cm×20cm的矩形瓷砖，可拼得一些长度不同但宽度均为20cm的图案．已知长度为10cm、20cm、30cm的所有图案如下：
【尝试操作】
如图，将小方格的边长看作10cm，请在方格纸中画出长度为40cm的所有图案．
【归纳发现】
观察以上结果，探究图案个数与图案长度之间的关系，将下表补充完整．

33. 我们学过用直尺和三角尺画平行线的方法，如图所示，直线a // b的根据是________．


34. 如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上．
（1）AB的长等于________；

（2）在△ABC的内部有一点P，满足S△PAB:S△PBC:S△PCA=1:2:3，请在如图所示的网格中，用无刻度的直尺，画出点P，并简要说明点P的位置是如何找到的（不要求证明）________．

35. 用直尺和圆规作△ABC，使BC＝a，AC＝b，∠B＝35∘，若这样的三角形只能作一个，则a，b间满足的关系式是________．

36. 如图，已知直线l1//l2 ，直线l3分别与l1、l2交于点A、B．请用尺规作图法，在线段AB上求作点P，使点P到l1、l2的距离相等．（保留作图痕迹，不写作法）


37. 如图4×4与6×6的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）

(1)选一个四边形画在图2中，使点P为它的一个顶点，并画出将它向右平移3个单位后所得的图形．

(2)选一个合适的三角形，将它的各边长扩大到原来的5倍，画在图3中．

38. 如图是由边长为1的小正方形构成的6×4的网格，点A，B均在格点上．

(1)在图1中画出以AB为边且周长为无理数的▱ABCD，且点C和点D均在格点上（画出一个即可）．

(2)在图2中画出以AB为对角线的正方形AEBF，且点E和点F均在格点上．

39. 如图，△ABC的顶点均在正方形网格格点上．只用不带刻度的直尺，作出△ABC的角平分线BD（不写作法，保留作图痕迹）


40. 如图，半圆形薄铁皮的直径AB=8，点O为圆心，C是半圆上一动点（不与A，B重合），连接AC并延长到点D，使AC=CD，过点D作B的垂线DH交CB，AB于点E，F，连接OC，记∠ABC=θ，θ随点C的移动而变化．

(1)移动点C，当点H，B重合时，求sinθ的值．

(2)当θ<45∘ 时，求证：BH⋅AH=DH⋅FF；

(3)当θ=45∘ 时，将扇形OAC剪下并卷成一个圆锥的侧面，求该圆锥的底面半径和高．
参考答案与试题解析
专题四十——尺规作图
一、 选择题 （本题共计 20 小题 ，每题 3 分 ，共计60分 ）
1.
【答案】
C
【考点】
作图—几何作图
平行线的判定
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
D
【考点】
作图—复杂作图
勾股定理
线段垂直平分线的性质
【解析】
①根据作图过程可得，四边形ADBE是菱形，再根据三角形中位线定理即可判断；
②根据菱形的四个边都相等，再根据勾股定理即可判断；
③根据三角形一边的中线分两个三角形面积相等即可判断；
④根据勾股定理先求出OF的长，再求出AD的长，进而可以得四边形ADBE的周长为25，进而即可判断．
【解答】
解：由题意可得，AO=BO，OE=OD，
∴ 四边形ADBE是平行四边形，
∵ DE⊥AB，
∴ 四边形ADBE是菱形，
∴ OF⊥AC，BC⊥AC，
∴ OF//BC，
又AO=BO，
∴ AF=CF，AG=GD，
∴ CD=2FG，故①正确；
∵ 四边形ADBE是菱形，
∴ AD=BD，
在Rt△ACD中，根据勾股定理，
得AD2−CD2=AC2，
∴ BD2−CD2=AC2，故②正确；
∵ 点G是AD的中点，
∴ S△AOD=2S△AOG，
∵ S△AOD=S△BOE，
则S△BOE=2S△AOG，故③正确；
∵ AF=12AC=12×6=3，
OF+OA=9，
∴ OA=9−OF，
在Rt△AFO中，根据勾股定理，
得(9−OF)2=OF2+32，
解得OF=4，
∴ OA=5，BC=8，
∴ AB=10，
BD+DC=AD+DC=8，
∴ CD=8−AD，
在Rt△ACD中，根据勾股定理，
得AD2=62+(8−AD)2，
解得AD=254，
∴ 菱形ADBE的周长为4AD=25，故④正确．
综上，正确的个数有4个.
故选D.
3.
【答案】
B
【考点】
等腰三角形的性质
角平分线的定义
作角的平分线
【解析】
根据等腰三角形的性质可得∠ACB的度数，观察作图过程可得，进而可得∠DCE的度数．
【解答】
解：∵ BA=BC，∠B=80∘，
∴ ∠A=∠ACB = 12(180∘−80∘)=50∘，
∴ ∠ACD=180∘−∠ACB=130∘，
观察作图过程可知：
CE平分∠ACD，
∴ ∠DCE = 12∠ACD=65∘，
∴ ∠DCE的度数为65∘.
故选B.
4.
【答案】
D
【考点】
作图—复杂作图
勾股定理
【解析】
根据作图过程可得AP是BD的垂直平分线，根据勾股定理可得BC的长，再根据等面积法求出AE的长，根据勾股定理可得BE的长，进而可得CD的长．
【解答】
解：∵ ∠BAC=90∘，AB=3，AC=4，
∴ BC=AB2+AC2=5，
根据作图过程可知：
AP是BD的垂直平分线，
∴ BE=DE，AE⊥BD，
∴ S△ABC=12AB⋅AC=12BC⋅AE，
∴ 5AE=12，
∴ AE=125，
在Rt△ABE中，根据勾股定理，得
BE=AB2−AE2=95，
∴ BD=2BE=185，
∴ CD=BC−BD=5−185=75．
故选D.
5.
【答案】
D
【考点】
垂径定理
作图—复杂作图
【解析】
如图，设OA交BC于T．解直角三角形求出AT，再在Rt△OCT中，利用勾股定理构建方程即可解决问题．
【解答】
解：如图，设OA交BC于T．
∵ AB=AC=25，AO平分∠BAC，
∴ AO⊥BC，BT=TC=4，
∴ AT=AC2−CT2=(25)2−42=2，
在Rt△OCT中，则有r2=(r−2)2+42，
解得r=5.
故选D.
6.
【答案】
C
【考点】
作图—应用与设计作图
作图—复杂作图
【解析】
此题暂无解析
【解答】
解：A选项，可直接得到AE=AB；
B选项作的∠ABC的角平分线，易得∠ABE=∠CBE，则可知∠ABE=∠AEB，得到AE=AB；
C选项无法证明；
D选项作了∠DAB的角平分线且与BC交于一点F，过点B作AF的垂直平分线交AD于点E，如图：
故AE=EF，因为∠AEB=∠EBF=∠BEF，所以BF=EF=AE，
综上可知四边形ABFE为菱形，所以AE=AB.
故选C.
7.
【答案】
D
【考点】
作图—复杂作图
平行线的判定
【解析】
根据平行线的判定方法一一判断即可．
【解答】
解：A，本选项作了角的平分线与等腰三角形，能得到一组内错角相等，从而可证两直线平行，故本选项不符合题意；
B，本选项作了一个角等于已知角，根据同位角相等两直线平行，能判断是过点P且与直线l的平行直线，本选项不符合题意；
C，由作图可知，垂直于同一条直线的两条直线平行，本选项不符合题意；
D，作图只截取了两条线段相等，而无法保证两直线平行的位置关系，本选项符合题意．
故选D.
8.
【答案】
C
【考点】
作角的平分线
角平分线的性质
【解析】
当SP⊥AB时，GP的值最小，根据尺规作图的方法可知，GB是∠ABC的角平分线，再根据角平分线的性质可知，当SP⊥AB时
GP=CG=
【解答】
解：由题意可知，当SP⊥AB时，GP的值最小，
根据尺规作图的方法可知，GB是2ABC的角平分线，
ΔC=90∘
∴ 兰:P⊥AB时，GP=CG=
故答案为：C．
9.
【答案】
C
【考点】
作图—复杂作图
【解析】
由PB+PC＝BC和PA+PC＝BC易得PA＝PB，根据线段垂直平分线定理的逆定理可得，点P在AB的垂直平分线上，进而得出结论．
【解答】
∵ PB+PC＝BC，而PA+PC＝BC，
∴ PA＝PB，
∴ 点P在AB的垂直平分线上，
即点P为AB的垂直平分线与BC的交点．
10.
【答案】
C
【考点】
平行线的判定
作一个角等于已知角
【解析】
根据平行线的判定，作一个角等于已知角的方法即可判断．
【解答】
解：由作图可知作图步骤为：
①以点O为圆心，任意长为半径画弧DM，分别交OA，OB于M，D；
②以点C为圆心，以OM为半径画弧EN，交OA于E；
③以点E为圆心，以DM为半径画弧FG，交弧EN于N；
④过点N作射线CP．
根据同位角相等两直线平行，可得CP // OB．
故选C.
11.
【答案】
D
【考点】
线段垂直平分线的性质
菱形的判定
矩形的判定
正方形的判定
梯形
作图—复杂作图
【解析】
根据四边相等的四边形是菱形即可判断．
【解答】
由作图可知：AC＝AD＝BC＝BD，
∴ 四边形ACBD是菱形，
12.
【答案】
C
【考点】
作角的平分线
角平分线的性质
【解析】
利用基本作图得到|AG平分∠BAC，利用角平分线的性质得到G点到AC的距离为1，然后根据三角形面积公式计算△ACG的面积．
【解答】
解：由作法得AG平分∠BAC
G点到AC的距离等于BG的长，即G点到AC的距离为1，
所以△ACG的面积=12×4×1=2
故选：C．
13.
【答案】
B
【考点】
作图—复杂作图
【解析】
由∠ADC＝2∠B且∠ADC＝∠B+∠BCD知∠B＝∠BCD，据此得DB＝DC，由线段的中垂线的性质可得答案．
【解答】
∵ ∠ADC＝2∠B且∠ADC＝∠B+∠BCD，
∴ ∠B＝∠BCD，
∴ DB＝DC，
∴ 点D是线段BC中垂线与AB的交点，
14.
【答案】
B
【考点】
反比例函数图象上点的坐标特征
线段垂直平分线的性质
作图—复杂作图
【解析】
如图，设OA交CF于K．利用面积法求出OA的长，再利用相似三角形的性质求出AB、OB即可解决问题；
【解答】
如图，设OA交CF于K．
由作图可知，CF垂直平分线段OA，
∴ OC=CA=1，OK=AK，
在Rt△OFC中，CF=OF2+OC2=5，
∴ AK=OK=1×25=255，
∴ OA=455，
由△FOC∽△OBA，可得OFOB=OCAB=CFOA，
∴ 2OB=1AB=5455，
∴ OB=85，AB=45，
∴ A(85, 45)，
∴ k=3225．
15.
【答案】
A
【考点】
平行线的判定与性质
等腰直角三角形
作图—复杂作图
【解析】
先利用等腰直角三角形的性质得出∠1=45∘，再利用平行线的性质即可得出结论；
【解答】
如图，
∵ △ABC是等腰直角三角形，
∴ ∠1=45∘，
∵ l // l′，
∴ ∠α=∠1=45∘，
16.
【答案】
D
【考点】
作图—复杂作图
【解析】
甲：根据作图可得AC=AP，利用等边对等角得：∠APC=∠ACP，由平角的定义可知：∠BPC+∠APC=180∘，根据等量代换可作判断；
乙：根据四边形的内角和可得：∠BPC+∠A=180∘．
【解答】
甲：如图1，∵ AC=AP，
∴ ∠APC=∠ACP，
∵ ∠BPC+∠APC=180∘
∴ ∠BPC+∠ACP=180∘，
∴ 甲错误；
乙：如图2，∵ AB⊥PB，AC⊥PC，
∴ ∠ABP=∠ACP=90∘，
∴ ∠BPC+∠A=180∘，
∴ 乙正确，
17.
【答案】
B
【考点】
作图—基本作图
角平分线的性质
作线段的垂直平分线
【解析】
试题分析：连接EG，由作图可知AD=AE，根据等腰三角形的性质可知AG是DE的垂直平分线，由平行四边形的性质可得出CDIIAB，故可得出∠2=∠3，据此可知AD=DG，由等腰三角形的性质可知OA=12AG，利用勾股定理求出OA的长即可．
连接EG
由作图可知AD=AE，AG是∠BAD的平分线，∠1=±2．AG⊥DEOD=12DE=3
四边形ABCD是平行四边形，CDIIAB，2=±3．∴ ．∠1=∠3．∴ AD=DG
AG⊥DE，∴ OA=12AG
在Rt△AOD中，OA=AD2−OD2=52−33=4，∴ AG=2AO=8
故选B．
【解答】
此题暂无解答
18.
【答案】
B
【考点】
作图—复杂作图
矩形的性质
【解析】
利用三角形的面积公式进而得出需P甲H＝P乙K＝2AB，即可得出答案．
【解答】
要使得△PBC的面积等于矩形ABCD的面积，
需P甲H＝P乙K＝2AB．
故两人皆错误．
19.
【答案】
B
【考点】
作图—复杂作图
切线的判定
【解析】
（甲）由OP＝BP，得出∠OBP＝∠BOP，所以∠OBP≠90∘，故（甲）错误；
（乙）根据线段的垂直平分线得出OB＝PB，OM＝PM，由已知条件OA＝2AP，得出OM=34OA=34OB，从而得出∠BOP＝∠BPO≠45∘，即∠OBP≠90∘，故（乙）错误；
【解答】
（甲）如图1，∵ 以P为圆心，OP长为半径画弧，交圆O于B点，
∴ OP＝BP，
∴ ∠OBP＝∠BOP，
∴ ∠OBP≠90∘，
∴ PB不是⊙O的切线，
∴ （甲）错误；
（乙）如图2，∵ 作OP的中垂线，交圆O于B点，交OP于M，
∴ OB＝PB，OM＝PM，
∵ OA＝2AP，
∴ OM=34OA=34OB，
∴ ∠BOP＝∠BPO≠45∘，
∴ ∠OBP≠90∘，
∴ （乙）错误，
20.
【答案】
B
【考点】
作图—复杂作图
角平分线的性质
线段垂直平分线的性质
【解析】
根据作法作图，及角平分线与中垂线的性质作答．
【解答】
解：依据题意画出右图
可得知∠1=∠2，AE=DE，
∴ ∠2=∠3，
∴ ∠1=∠3，即DE // AB．
故选B．
二、 填空题 （本题共计 15 小题 ，每题 3 分 ，共计45分 ）
21.
【答案】
1+2
【考点】
作角的平分线
等腰三角形的判定
【解析】
此题暂无解析
【解答】
此题暂无解答
22.
【答案】
2或27
【考点】
作线段的垂直平分线
勾股定理
等边三角形的性质
线段垂直平分线的性质
【解析】
由作图知，点D在AC的垂直平分线上，得到点B在AC的垂直平分线上，求得BD垂直平分AC，设垂足为E，得到BE=3，当点D、B在AC的两侧时，如图，当点D、B在AC的同侧时，如图，解直角三角形即可得到结论．
【解答】
解：由作图知，点D在AC的垂直平分线上，
∵ △ABC是等边三角形，
∴ 点B在AC的垂直平分线上，
∴ BD垂直平分AC，
设垂足为E，
∵ AC=AB=2，
∴ BE=3，
当点D、B在AC的两侧时，
∵ BD=23，
∴ BE=DE，
∴ AD=AB=2，
∴ m=2；
当点D、B在AC的同侧时，
∵ BD′=23，
∴ D′E=33，
∴ AD′=(33)2+12=27，
∴ m=27，
综上所述，m的值为2或27.
故答案为：2或27.
23.
【答案】
2425
【考点】
作角的平分线
锐角三角函数的定义
菱形的判定与性质
【解析】
如图，连接DB，过点D作DH⊥ON于H．首先证明四边形AOBD是菱形，解直角三角形求出DH即可解决问题．
【解答】
解：如图，连接DB，过点D作DH⊥ON于H．
由作图可知，∠AOD=∠DOE，OA=OB，
∵ AD // EO，
∴ ∠ADO=∠DOE，
∴ ∠AOD=∠ADO，
∴ AO=AD，
∴ AD=OB，AD // OB，
∴ 四边形AOBD是菱形，
∴ OB=BD=OA=10，BD // OA，
∴ ∠MON=∠DBE，∠BOD=∠BDO，
∵ DE⊥OD，
∴ ∠BOD+∠DEO=90∘，∠ODB+∠BDE=90∘，
∴ ∠BDE=∠BED，
∴ BD=BE=10，
∴ OE=2OB=20，
∴ OD=OE2−DE2=202−122=16，
∵ DH⊥OE，
∴ DH=OD⋅DEEO=16×1220=485，
∴ sin∠MON=sin∠DBH=DHDB=48510=2425.
故答案为：2425.
24.
【答案】
13
如图，取格点M，N，连接MN，连接BD并延长，与MN相交于点B′，连接B′C，与半圆相交于点E，连接BE，与AC相交于点P，连接B′P并延长，与BC相交于点Q，则点P，Q即为所求．
【考点】
勾股定理
轴对称——最短路线问题
作图—复杂作图
【解析】
(Ⅰ)利用网格根据勾股定理即可求出线段AC的长；
（Ⅱ)取格点M，N，连接MN，连接BD并延长，与MN相交于点B′，连接B′C，与半圆相交于点E，连接BE，与AC相交于点P，连接B′P并延长，与BC相交于点Q，即可得点P，Q．
【解答】
解：线段AC的长等于32 + 22 = 13.
故答案为：13.
(2)如图，取格点M，N，连接MN，连接BD并延长，与MN相交于点B′，连接B′C，与半圆相交于点E，连接BE，与AC相交于点P，连接B′P并延长，与BC相交于点Q，则点P，Q即为所求．
故答案为：如图，取格点M，N，连接MN，连接BD并延长，与MN相交于点B′，连接B′C，与半圆相交于点E，连接BE，与AC相交于点P，连接B′P并延长，与BC相交于点Q，则点P，Q即为所求．
25.
【答案】
3
【考点】
作角的平分线
角平分线的性质
坐标与图形性质
【解析】
根据作图方法可知点P在∠BOA的角平分线上，由角平分线的性质可知点P到x轴和y轴的距离相等，结合点P在第一象限，可得关于a的方程，求解即可．
【解答】
解：∵ OA=OB，分别以点A，B为圆心，以大于12AB长为半径画弧，两弧交于点P，
∴ 点P在∠BOA的角平分线上，
∴ 点P到x轴和y轴的距离相等，
又∵ 点P在第一象限，点P的坐标为(a, 2a−3)，
∴ a=2a−3，
∴ a=3.
故答案为：3.
26.
【答案】
45∘
【考点】
线段垂直平分线的性质
菱形的性质
作线段的垂直平分线
【解析】
根据∠EBD＝∠ABD−∠ABE，求出∠ABD，∠ABE即可解决问题．
【解答】
解：∵ 四边形ABCD是菱形，
∴ AD=AB，
∴ ∠ABD=∠ADB=12(180∘−∠A)=75∘.
由作图可知，EA=EB，
∴ ∠ABE=∠A=30∘，
∴ ∠EBD=∠ABD−∠ABE=75∘−30∘=45∘.
故答案为：45∘.
27.
【答案】
5,8,N,m＝4a
【考点】
二元一次方程组的应用——行程问题
二元一次方程组的应用——其他问题
二元一次方程的应用
作图—复杂作图
实数
在数轴上表示实数
数轴
【解析】
（1）根据数轴上点A对应−3，点B对应1，求得AB的长，进而根据AB＝BC可求得AC的长以及点C表示的数；
（2）可设原点为O，根据条件可求得AB中点表示的数以及线段AB的长度，根据AB＝2，可得AQ＝BQ＝1，结合OQ的长度即可确定N为数轴的原点；
（3）设AB的中点为M，先求得AB的长度，得到AM＝BM＝n，根据线段垂直平分线的作法作图即可；
（4）①根据每分钟进校人数为b，每个通道每分钟进入人数为a，列方程组m+4b=12am+2b=8a ，根据m+2b＝OF，m+4b＝12a，即可画出F，G点，其中m+2b表示两分钟后，校门口需要进入学校的学生人数；
②解①中的方程组，即可得到m＝4a．
【解答】
（2）【找一找】：记原点为O，
∵ AB=22+1−(22−1)＝2，
∴ AQ＝BQ＝1，
∴ OQ＝OB−BQ=22+1−1=22，
∴ N为原点．
故答案为：N．
（3）【画一画】：记原点为O，
由AB＝c+n−(c−n)＝2n，
作AB的中点M，
得AM＝BM＝n，
以点O为圆心，
AM＝n长为半径作弧交数轴的正半轴于点E，
则点E即为所求（1）
（4）【用一用】：在数轴上画出点F，G；2分钟后，校门口需要进入学校的学生人数为：m＝4a．
∵ 4分钟内开放3个通道可使学生全部进校，
∴ m+4b＝3×a×4，即m+4b＝12a(Ⅰ)(2)∵ 2分钟内开放4个通道可使学生全部进校，
∴ m+2b＝4×a×2，即m+2b＝8a(Ⅱ)(3)①以O为圆心，OB长为半径作弧交数轴的正半轴于点F，则点F即为所求．
作OB的中点E，则OE＝BE＝4a，在数轴负半轴上用圆规截取OG＝3OE＝12a，
则点G即为所求．
+(m+2b)的实际意义：2分钟后，校门口需要进入学校的学生人数（4）②方程(Ⅱ)×2−方程(Ⅰ)得：m＝4a．
故答案为：m＝4a．
28.
【答案】
55∘．
【考点】
直角三角形的性质
余角和补角
线段垂直平分线的性质
作角的平分线
【解析】
根据直角三角形两锐角互余得∠BAC=70∘，由角平分线的定义得∠2=35∘，由线段垂直平分线可得△AOM是直角三角形，故可得
∠1+2=90∘，从而可得∠1=55∘，最后根据对顶角相等求出α
【解答】
如图，
△ABC是直角三角形，∠C=90∘
∠B+∠BAC=90∘
．∠B=20∘
∠BAC=90∘−∠B=90∘−20∘=70∘
AM是∠BAC的平分线，
．∠2=12∠BAC=12×70∘=35∘
：PQ是AB的垂直平分线，
．4MO．是直角三角形，
∠1+∠2=90∘
∠1=90∘−∠2=90∘−35∘=5.5∘
∠α与∠1是对顶角，
∠α=∠1=55∘
故答案为：55∘
29.
【答案】
32
【考点】
线段垂直平分线的性质
作图—复杂作图
【解析】
由作图可得MN是线段AB的垂直平分线，BD是∠ABC的平分线，根据它们的性质可得∠A＝∠ABD＝∠CBD，再根据三角形内角和定理即可得解．
【解答】
由作图可得，MN是线段AB的垂直平分线，BD是∠ABC的平分线，
∴ AD＝BD，，
∴ ∠A＝∠ABD，
∴ ∠A＝∠ABD＝∠CBD，
∵ ∠A+∠ABC+∠C＝180∘，且∠C＝84∘，
∴ ∠A+2∠ABD＝180∘−∠C，
即3∠A＝180∘−84∘，
∴ ∠A＝32∘．
30.
【答案】
4
【考点】
作图—复杂作图
平行四边形的性质
三角形中位线定理
【解析】
利用作法得到∠COE=∠OAB，则OE // AB，利用平行四边形的性质判断OE为△ABC的中位线，从而得到OE的长．
【解答】
解：由作法得∠COE=∠OAB，
∴ OE // AB.
∵ 四边形ABCD为平行四边形，
∴ OC=OA，
∴ CE=BE，
∴ OE为△ABC的中位线，
∴ OE=12AB=12×8=4．
故答案为：4.
31.
【答案】
172
(2)如图，取圆与网格的交点E，F，连接EF与AC交于一点，
则这一点是圆心O，AB与网格线相交于D，
连接DO并延长交⊙O于点Q，连接QC并延长，与B，O的连线相交于点P，连接AP，
则点P满足∠PAC=∠PBC=∠PCB.
【考点】
圆周角定理
作图—复杂作图
勾股定理
【解析】
(Ⅰ)根据勾股定理即可得到结论；
(Ⅱ)如图，取圆与网格的交点E，F，连接EF与AC交于一点，则这一点是圆心O，AB与网格线相交于D，连接DO并延长交⊙O于点Q，连接QC并延长，与B，O的连线相交于点P，连接AP，于是得到结论．
【解答】
解：(1)因为在每个小正方形的边长为1的网格中，△ABC的顶点A在格点上，B是小正方形边的中点，
所以AB=22+(12)2=172
故答案为：172.
(2)如图，取圆与网格的交点E，F，连接EF与AC交于一点，
则这一点是圆心O，AB与网格线相交于D，
连接DO并延长交⊙O于点Q，连接QC并延长，与B，O的连线相交于点P，连接AP，
则点P满足∠PAC=∠PBC=∠PCB.
32.
【答案】
5,8,13
【考点】
作图—应用与设计作图
【解析】
根据已知条件作图可知40cm时，所有图案个数5个；猜想得到结论；
【解答】
如图
根据作图可知40cm时，所有图案个数5个
50cm时，所有图案个数8个；
60cm时，所有图案个数13个；
33.
【答案】
同位角相等，两直线平行
【考点】
平行线的判定与性质
作图—复杂作图
【解析】
关键题意得出∠1=∠2；∠1和∠2是同位角；由平行线的判定方法即可得出结论．
【解答】
如图所示：
根据题意得出：∠1=∠2；∠1和∠2是同位角；
∵ ∠1=∠2，
∴ a // b（同位角相等，两直线平行）；
故答案为：同位角相等，两直线平行．
34.
【答案】
17
如图AC与网格相交，得到点D、E，取格点F，连接FB并且延长，与网格相交，得到M，N．连接DN，EM，DN与EM相交于点P，点P即为所求．
【考点】
勾股定理
作图—应用与设计作图
【解析】
（1）利用勾股定理即可解决问题；
（2）如图AC与网格相交，得到点D、E，取格点F，连接FB并且延长，与网格相交，得到M，N，G．连接DN，EM，DG，DN与EM相交于点P，点P即为所求．
【解答】
AB=12+42=17．
故答案为17．
如图AC与网格相交，得到点D、E，取格点F，连接FB并且延长，与网格相交，得到M，N，G．连接DN，EM，DG，DN与EM相交于点P，点P即为所求．
理由：平行四边形ABME的面积：平行四边形CDNB的面积：平行四边形DEMG的面积=1:2:3，
△PAB的面积=12平行四边形ABME的面积，△PBC的面积=12平行四边形CDNB的面积，△PAC的面积=△PNG的面积=12△DGN的面积=12平行四边形DEMG的面积，
∴ S△PAB:S△PBC:S△PCA=1:2:3．
35.
【答案】
sin35∘=ba或b≥a
【考点】
解直角三角形
作图—复杂作图
切线的性质
【解析】
首先画BC＝a，再以B为顶点，作∠ABC＝35∘，然后再以点C为圆心、b为半径画圆弧交AB于点A，然后连接AC即可，①当AC⊥AB时，②当b≥a时三角形只能作一个．
【解答】
如图所示：
若这样的三角形只能作一个，则a，b间满足的关系式是：①当AC⊥AB时，即sin35∘=ba；②当b≥a时．
故答案为：sin35∘=ba或b≥a．
三、 解答题 （本题共计 5 小题 ，每题 10 分 ，共计50分 ）
36.
【答案】
解：如图所示，点P即为所求．
【考点】
作线段的垂直平分线
作图—复杂作图
角平分线的性质
【解析】
此题暂无解析
【解答】
解：如图所示，点P即为所求．
37.
【答案】
解：（1）如图2所示，即为所求；
（2）如图3所示，即为所求．
【考点】
作图—应用与设计作图
解直角三角形
勾股定理
【解析】
此题暂无解析
【解答】
解：（1）如图2所示，即为所求；
（2）如图3所示，即为所求．
38.
【答案】
解：(1)
(2)
【考点】
作图—复杂作图
平行四边形的性质
数轴
【解析】
此题暂无解析
【解答】
解：(1)
(2)
39.
【答案】
解：如图，射线BD即为所求作，
【考点】
作图—复杂作图
等腰三角形的判定与性质
【解析】
此题暂无解析
【解答】
解：如图，射线BD即为所求作，
40.
【答案】
【考点】
经过一点作已知直线的垂线
等腰三角形的判定
【解析】
此题暂无解析
【解答】
此题暂无解答如图，已知直线l1,l2,l3,l4，若∠1=∠2，则∠3=∠4．
请完成下面的说理过程．
解：已知∠1=∠2
根据（内错角相等，两直线平行），得l1//l2 ．
再根据（________※________），得∠3=∠4．
图案的长度
10cm
20cm
30cm
40cm
50cm
60cm
所有不同图案的个数
1
2
3
________
________
________