2020-2021学年第四章 三角形2 图形的全等精品课件ppt

这是一份2020-2021学年第四章 三角形2 图形的全等精品课件ppt，文件包含北师大版七年级数学下册42图形的全等课件pptx、北师大版七年级数学下册42图形的全等docx等2份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

1.了解全等形及全等三角形的概念，掌握全等三角形的表示方法，理解和掌握全等三角形的性质; 2.了解对应边和对应角的概念，能准确找到全等三角形对应边和对应角;
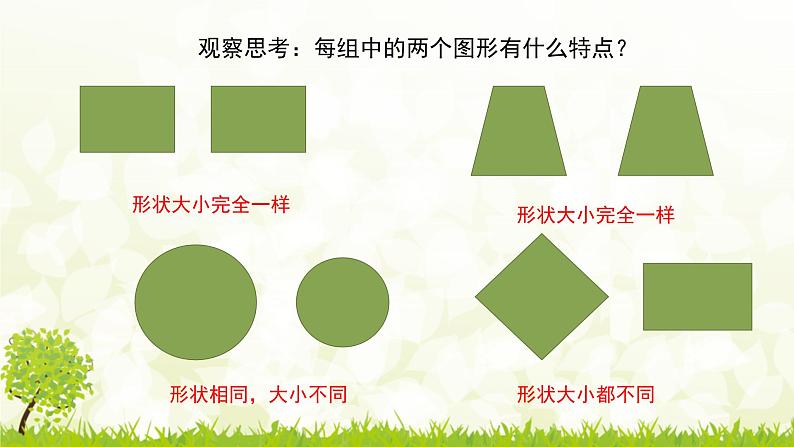
下列各组图形的形状与大小有什么特点？
观察思考：每组中的两个图形有什么特点？
能够完全重合的两个图形叫做全等图形.
如果两个图形全等，它们的形状和大小一定都相等
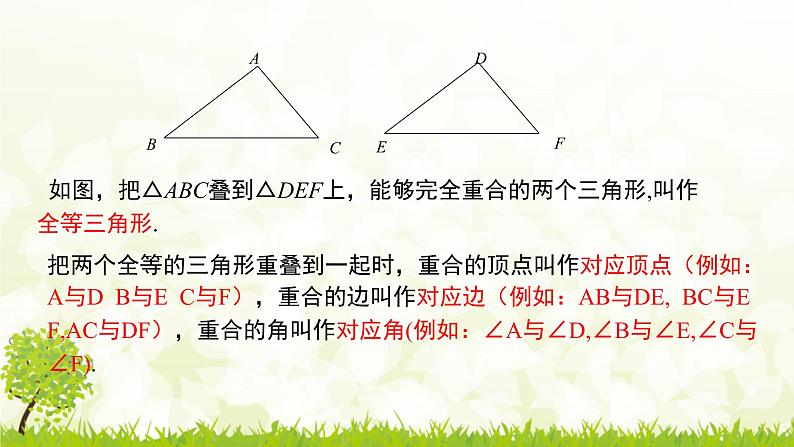
如图，把△ABC叠到△DEF上，能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时，重合的顶点叫作对应顶点（例如：A与D B与E C与F），重合的边叫作对应边（例如：AB与DE, BC与E F,AC与DF），重合的角叫作对应角(例如：∠A与∠D,∠B与∠E,∠C与∠F).
“全等”用符号“≌”表示，读作“全等于”.
注意：记两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上.
说说下列全等图形的对应角以及对应边？
对应边、对应角有什么规律?
我们知道能够完全重合的两个三角形,叫作全等三角形.既然两个图形重合，你能否得出全等图形的性质？
全等三角形的对应边相等；全等三角形的对应角相等.
∴A B=F D，A C=F E，B C=D E（全等三角形对应边相等）
∠A=∠F，∠B=∠D，∠C=∠E（全等三角形对应角相等）
能够 的两个图形叫做全等形.两个三角形 重合时，互相 的顶点叫做对应顶点.记两个全等三角形时，通常把表示 顶点的字母写在 的位置上.
1. 有公共边，则公共边为对应边；
3.最大边与最大边（最小边与最小边）为对应边；最大角与最大角（最小角与最小角）为对应角；
4. 对应角的对边为对应边；对应边的对角为对应角.
2. 有公共角（对顶角），则公共角(对顶角)为对应角；
对应角以及对应边规律总结
下列说法：①全等图形的形状相同、大小相等；②全等三角形的对应边相等；③全等三角形的周长、面积分别相等；④面积相等的两个三角形全等，其中正确的说法为（　　）A．①③④B．②③④C．①②③D．①②③④
如图，△ABC≌△CDA，并且BC＝DA，那么下列结论错误的是（　　）
A．∠1＝∠2 B．AC＝CAC．AB＝AD D．∠B＝∠D
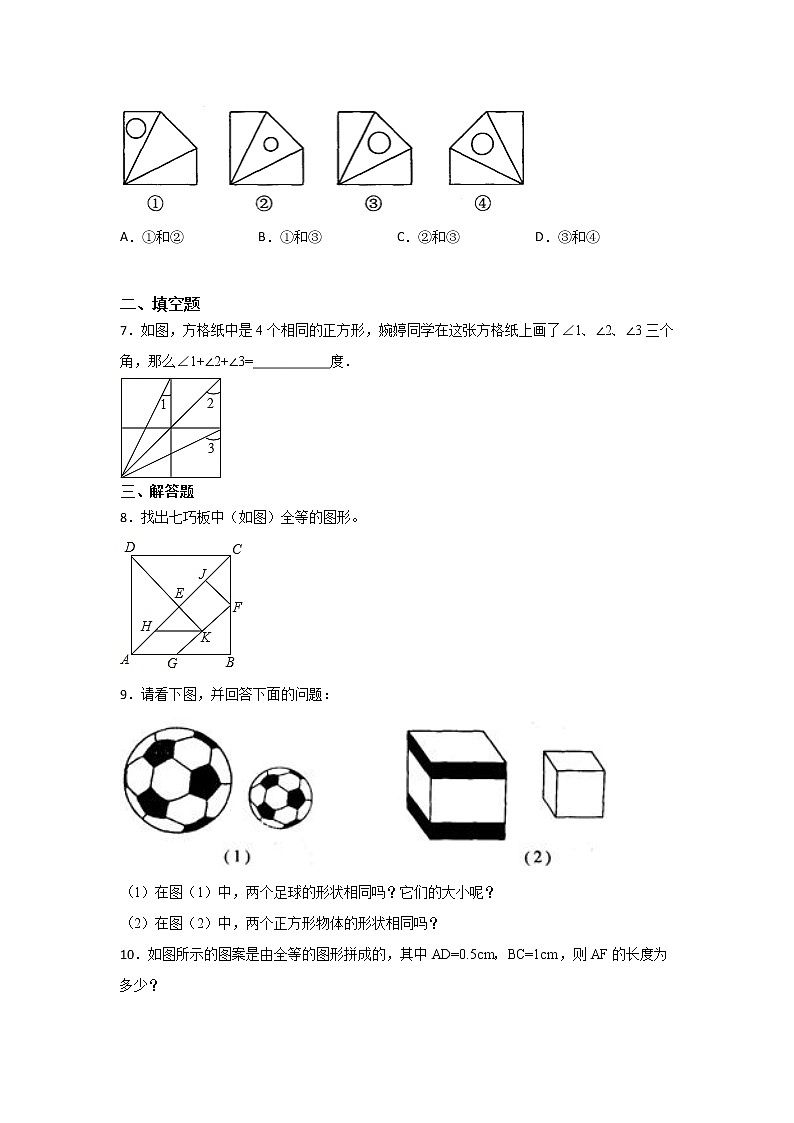
如图，在4×4的正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为（　　）
A．300°B．315°C．320°D．325°
下列说法错误的有（　　）①只有两个三角形才能完全重合；②如果两个图形全等，它们的形状和大小一定都相同；③两个正方形一定是全等图形；④边数相同的图形一定能互相重合．A．4个B．3个C．2个D．1个
如图，△ABC≌△DFE，点B、E、C、F在同一直线上，BE＝2cm，BF＝11cm，则EC的长度是__________．
∵△ABC≌△DFE，∴BC=EF∴BC-EC=EF-EC∴CF=BE=2cm，∴EC=BF-CF-BE=7cm，
如图，△ABC是等边三角形，边长为6厘米，将△ABC沿直线BC向右平移4.5厘米到△DEF的位置．
（1）求∠ADF的度数；（2）求四边形ABFD的周长．
全等形：能够完全重合的两个图形叫作全等形.
全等三角形：能够完全重合的两个三角形叫作全等三角形.
全等三角形的对应边相等
全等三角形的对应角相等