2020-2021学年某校初二（上）10月月考数学试卷 (1)

这是一份2020-2021学年某校初二（上）10月月考数学试卷 (1)，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 如图，三角形的个数是( )

A.6个B.5个C.4个D.3个

2. 要组成一个三角形，三条线段的长度可取( )
A.3，4，5B.2，3，5C.1，2，3D.3，5，10

3. 适合条件∠A=∠B=12∠C的△ABC是( )
A.锐角三角形B.直角三角形C.钝角三角形D.不能确定

4. 从n边形的一个顶点引对角线，可以将这个n边形分成的三角形的个数为( )
A.n−3B.n−2C.n−1D.n

5. 下列正多边形材料中，不能单独用来铺满地面的是( )
A.正三角形B.正四边形C.正五边形D.正六边形

6. 下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等

7. 如图，将两根钢条AA′，BB′的中点O连在一起，使AA′，BB′可以绕着点O自由旋转，就做成了一个测量工件，则A′B′的长等于内槽宽AB，那么判定△OAB≅△OA′B′的理由是( )

A.SASB.ASAC.SSSD.AAS

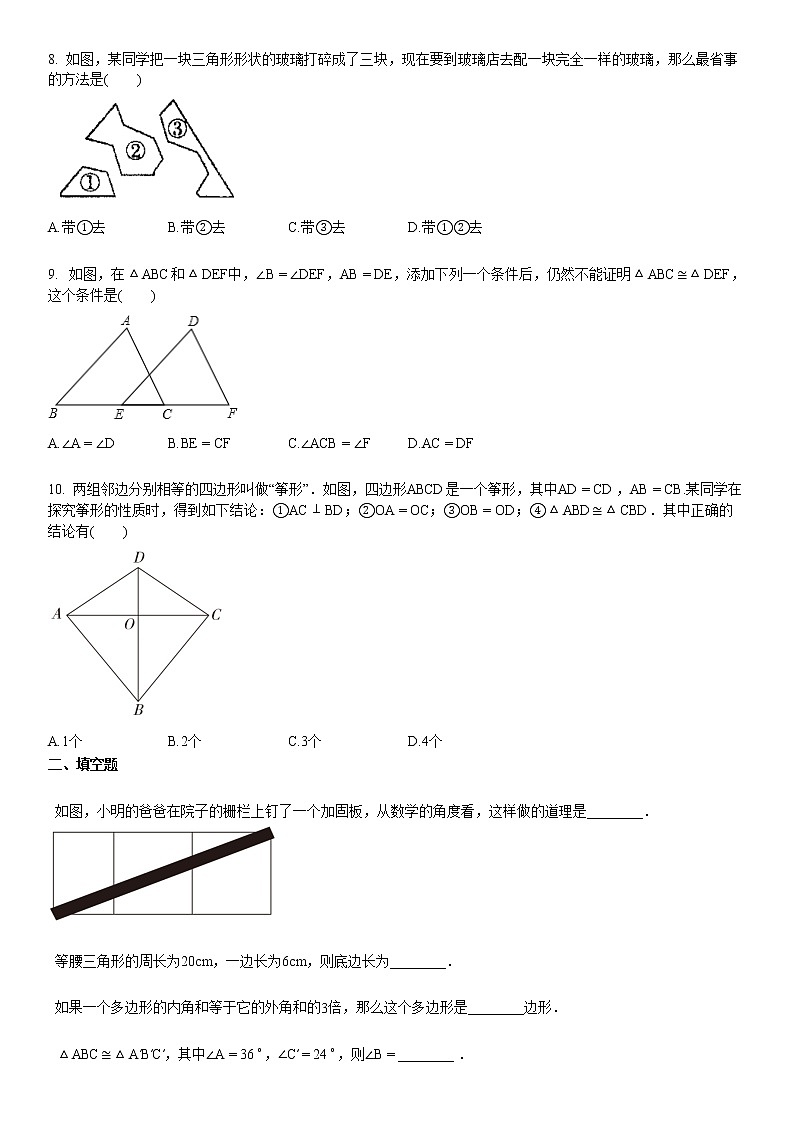
8. 如图，某同学把一块三角形形状的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是( )

A.带①去B.带②去C.带③去D.带①②去

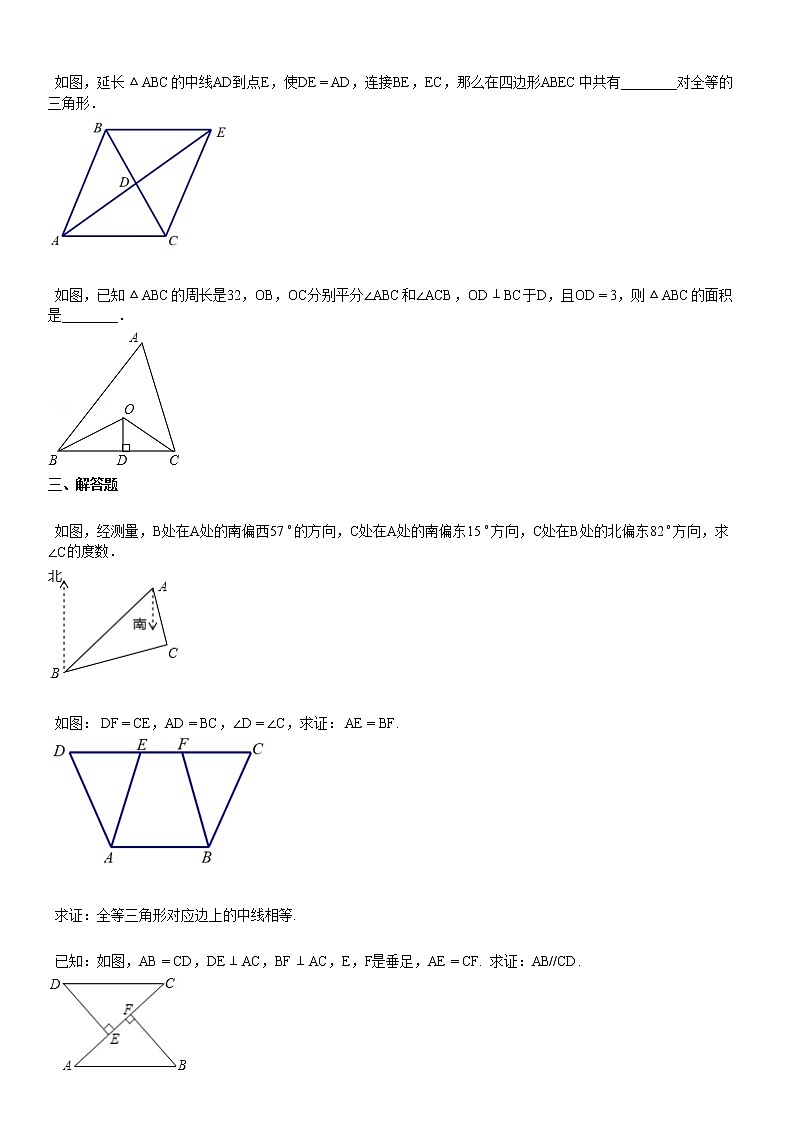
9. 如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≅△DEF，这个条件是( )

A.∠A=∠DB.BE=CFC.∠ACB=∠FD.AC=DF

10. 两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AD=CD ，AB=CB.某同学在探究筝形的性质时，得到如下结论：①AC⊥BD；②OA=OC；③OB=OD；④△ABD≅△CBD．其中正确的结论有( )

A.1个B.2个C.3个D.4个
二、填空题

如图，小明的爸爸在院子的栅栏上钉了一个加固板，从数学的角度看，这样做的道理是________．


等腰三角形的周长为20cm，一边长为6cm，则底边长为________．

如果一个多边形的内角和等于它的外角和的3倍，那么这个多边形是________边形．

△ABC≅△A′B′C′，其中∠A=36∘，∠C′=24∘，则∠B=________ ．

如图，延长△ABC的中线AD到点E，使DE=AD，连接BE，EC，那么在四边形ABEC中共有________对全等的三角形．


如图，已知△ABC的周长是32，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是________．

三、解答题

如图，经测量，B处在A处的南偏西57∘的方向，C处在A处的南偏东15∘方向，C处在B处的北偏东82∘方向，求∠C的度数．


如图： DF=CE，AD=BC，∠D=∠C，求证： AE=BF.


求证：全等三角形对应边上的中线相等.

已知：如图，AB=CD，DE⊥AC，BF⊥AC，E，F是垂足，AE=CF. 求证：AB//CD.


如图，在△ABC中，AB=AC，AC边上的中线把三角形的周长分为24和30的两部分，求三角形各边的长.


如图，△ABC中，∠A=40∘，∠B=72∘，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，求∠CDF的度数．


如图，工人师傅要检查人字梁的∠B和∠C是否相等，但他手边没有量角器，只有一个刻度尺．他是这样操作的：①分别在BA和CA上取BE=CG；②在BC上取BD=CF；③量出DE的长am，FG的长bm．如果a=b，则说明∠B和∠C是相等的，他的这种做法合理吗？为什么？


如图，在四边形ABCD中，∠B=∠C=90∘，点O是BC的中点，OA平分∠BAD.

(1)求证：OD平分∠ADC；

(2)试探究线段AB，CD，AD之间的关系．

已知：Aa,0，B0,b，其中a，b满足2a+b+42+a−b+8=0，C是x轴正半轴上一动点，连接BC，过A作AD⊥BC于D，交y轴于E.

(1)求A，B两点的坐标；

(2)如图1，若C点坐标为2,0，求E点坐标；

(3)如图2，连接OD，当C在x轴正半轴上运动时， ∠ADO的的度数是否发生变化？若变化求出变化范围；若不变化，求出取值．
参考答案与试题解析
2020-2021学年湖北省十堰市某校初二（上）10月月考数学试卷
一、选择题
1.
【答案】
B
【考点】
三角形
【解析】
将所有三角形列举出来即可求得个数.
【解答】
解：图中的三角形有：△ABE，△ABC，△BCE，△BCD，△CDE共5个.
故选B.
2.
【答案】
A
【考点】
三角形三边关系
【解析】
根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边．就可以判断．
【解答】
解：在三角形中任意两边之和大于第三边，任意两边之差小于第三边．
A，能组成三角形，此选项正确；
B，2+3=5，不能组成三角形，故此选项错误；
C，1+2=3，不能组成三角形，故此选项错误；
D，3+5<10，不能组成三角形，故此选项错误.
故选A．
3.
【答案】
B
【考点】
三角形内角和定理
直角三角形的性质
【解析】
根据三角形内角和定理个已知得出关于∠C的方程，求出∠C的度数，即可得出答案．
【解答】
解：∵ ∠A=∠B=12∠C，
∠A+∠B+∠C=180∘，
∴ 12∠C+12∠C+∠C=180∘，
∴ ∠C=90∘，
∴ △ABC是直角三角形.
故选B．
4.
【答案】
B
【考点】
多边形的对角线
【解析】
可根据n边形从一个顶点引出的对角线与边的关系：n−3，可分成(n−2)个三角形直接判断．
【解答】
解：多边形有n条边，则经过多边形的一个顶点的所有对角线有(n−3)条，经过n边形的一个顶点的所有对角线把多边形分成(n−2)个三角形．
故选B．
5.
【答案】
C
【考点】
平面镶嵌（密辅）
【解析】
利用平面图形的镶嵌对题目进行判断即可得到答案，需要熟知用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做平面图形的镶嵌．
【解答】
解：A，正三角形的每个内角是60∘，能整除360∘，能密铺；
B，正四边形的每个内角是90∘，4个能密铺；
C，正五边形每个内角是180∘−360∘÷5=108∘，不能整除360∘，不能密铺；
D，正六边形的每个内角是120∘，能整除360∘，3个能密铺．
故选C．
6.
【答案】
C
【考点】
全等图形
【解析】
根据全等形的概念：能够完全重合的两个图形叫做全等形，以及全等三角形的判定定理可得答案．
【解答】
解：A、形状相同的两个三角形全等，说法错误，
应该是形状相同且大小也相同的两个三角形全等；
B、面积相等的两个三角形全等，说法错误；
C、完全重合的两个三角形全等，说法正确；
D、所有的等边三角形全等，说法错误.
故选C．
7.
【答案】
A
【考点】
全等三角形的判定
【解析】
由O是AA′、BB′的中点，可得AO=A′O，BO=B′O，再有∠AOA′=∠BOB′，可以根据全等三角形的判定方法SAS，判定△OAB≅△OA′B′．
【解答】
解：∵ O是AA′，BB′的中点，
∴ AO=A′O，BO=B′O，
在△OAB和△OA′B′中，
AO=A′O，∠AOB=∠A′OB′,BO=B′O，
∴ △OAB≅△OA′B′(SAS).
故选A．
8.
【答案】
C
【考点】
全等三角形的性质
【解析】
根据全等三角形的判定，已知两角和夹边，就可以确定一个三角形．
【解答】
解：第③块玻璃不仅保留了圆三角信号的两个角还保留了一边，则可以根据ASA来匹配一块一样的玻璃.
故选C．
9.
【答案】
D
【考点】
全等三角形的判定
【解析】
根据全等三角形的判定，利用ASA、SAS、AAS即可得答案．
【解答】
解：∠B=∠DEF，AB=DE.
A，添加∠A=∠D，利用ASA可得△ABC≅△DEF，故A正确；
B，添加BE=CF，可得BC=EF，利用SAS可得△ABC≅△DEF，故B正确；
C，添加∠ACB=∠F，利用AAS可得△ABC≅△DEF，故C正确；
D，添加AC=DF，不能证明△ABC≅△DEF，故D错误.
故选D．
10.
【答案】
C
【考点】
全等三角形的性质与判定
全等三角形的性质
【解析】
利用全等三角形的判定和性质进行求解即可.
【解答】
解：在△ABD与△CBD中，
∵ AD=CD，AB=BC，DB=DB，
∴ △ABD≅△CBDSSS，故④正确；
∴ ∠ADB=∠CDB.
在△AOD与△COD中，
∵ AD=CD，∠ADB=∠CDB，OD=OD，
∴ △AOD≅△CODSAS，
∴ ∠AOD=∠COD=90∘，AO=OC，
∴ AC⊥DB，故①②正确；
由题意不能得到OB=OD，故③错误.
综上所述，正确结论有①②④，共3个．
故选C．
二、填空题
【答案】
三角形具有稳定性
【考点】
三角形的稳定性
【解析】
在院子的门板上钉了一个加固板，形成了两个三角形，这种做法根据的是三角形的稳定性．
【解答】
解：这样做形成了两个三角形，做的道理是三角形具有稳定性．
故答案为：三角形具有稳定性.
【答案】
6cm或8cm
【考点】
三角形三边关系
等腰三角形的判定与性质
【解析】
分6cm是底边与腰长两种情况讨论求解．
【解答】
解：①6cm是底边时，
腰长=12×(20−6)=7cm，
此时三角形的三边分别为7cm，7cm，6cm，能组成三角形；
②6cm是腰长时，底边=20−6×2=8cm，
此时三角形的三边分别为6cm，6cm，8cm，能组成三角形.
综上所述，底边长为6cm或8cm．
故答案为：6cm或8cm．
【答案】
八
【考点】
多边形内角与外角
【解析】
根据多边形的内角和定理，多边形的内角和等于(n−2)⋅180∘，外角和等于360∘，然后列方程求解即可．
【解答】
解：设多边形的边数是n，
根据题意得，(n−2)⋅180∘=3×360∘，
解得n=8，
∴ 这个多边形为八边形．
故答案为：八．
【答案】
120∘
【考点】
全等三角形的性质
【解析】
掌握全等三角形的性质是解答本题的根本，需要知道全等三角形的对应边相等; 全等三角形的对应角相等．
【解答】
解：∵ △ABC≅△A′B′C′，
∴ ∠C=∠C′=24∘，
∴ ∠B=180∘−∠A−∠C=120∘.
故答案为：120∘．
【答案】
4
【考点】
全等三角形的性质与判定
【解析】
利用全等三角形的判定证明即可.
【解答】
解：∵AD是△ABC的中线，
∴BD=CD.
在△ADC和△EDB中，
∵ ED=AD，∠ADC=∠EDB，BD=CD，
∴ △ADC≅△EDB(SAS)，
∴AC=EB，ED=AD.
在△ADB和△EDC中，
ED=AD，∠ADB=∠EDC，BD=CD，
∴ △ADB≅△EDCSAS，
∴AB=EC.
在△ABC和△ECB中，
AB=EC，AC=EB，BC=CB，
∴ △ABC≅△ECBSSS.
在△ABE和△ECA中，
AB=EC，AC=EB，AE=EA，
∴ △ABE≅△ECASSS，
共4对全等三角形．
故答案为：4.
【答案】
48
【考点】
三角形的面积
角平分线的性质
【解析】
过O作OM⊥AB，ON⊥AC，连接AO，根据角平分线的性质可得OM＝ON＝OD，再求出△ABO，△BCO，△ACO的面积和即可．
【解答】
解：过O作OE⊥AB于E，OF⊥AC于F，连接OA，
∵ OB，OC分别平分∠ABC和∠ACB，OD⊥BC，
∴ OE=OD，OD=OF，即OE=OF=OD=3，
∴ S△ABC =S△AOB +S△AOC +S△OBC
=12×AB×OE+12×AC×OF+12×BC×OD
=12×3×(AB+AC+BC)
=12×3×32
=48．
故答案为：48．
三、解答题
【答案】
解：如图所示，
因为BD // AE，
所以∠DBA=∠BAE=57∘，
所以∠ABC=∠DBC−∠DBA=82∘−57∘=25∘．
在△ABC中，∠BAC=∠BAE+∠CAE
=57∘+15∘=72∘，
所以∠C=180∘−∠ABC−∠BAC
=180∘−25∘−72∘=83∘．
【考点】
三角形内角和定理
方向角
【解析】
根据平行线的性质，可得内错角相等，根据角的和差，可得∠ABC、∠BAC，根据三角形的内角和公式，可得答案．
【解答】
解：如图所示，
因为BD // AE，
所以∠DBA=∠BAE=57∘，
所以∠ABC=∠DBC−∠DBA=82∘−57∘=25∘．
在△ABC中，∠BAC=∠BAE+∠CAE
=57∘+15∘=72∘，
所以∠C=180∘−∠ABC−∠BAC
=180∘−25∘−72∘=83∘．
【答案】
证明：∵ DF=CE，
∴ DF−EF=CE−EF，
∴ DE=CF.
在△ADE和△BCF中，
∵AD=BC，∠D=∠C，DE=CF，
∴ △ADE≅△BCFSAS，
∴ AE=BF.
【考点】
全等三角形的性质与判定
【解析】
∵ DF=CE，∴ DF−EF=CF−EF，∴ DE=CF，
在△ADE和△BCP中，AD=BC∠D=∠CDE=CF，
∴ △ADE≅△BCFSAS ，∴ AE=BF .
【解答】
证明：∵ DF=CE，
∴ DF−EF=CE−EF，
∴ DE=CF.
在△ADE和△BCF中，
∵AD=BC，∠D=∠C，DE=CF，
∴ △ADE≅△BCFSAS，
∴ AE=BF.
【答案】
证明：如图：
∵ △ABC≅△DEF ，
∴ AB=DE，∠B=∠E，BC=EF.
∵ AM，DN分别是BC和EF边上的中线，
∴ BM=12BC，EN=12EF ，
∴ BM=EN.
在△ABM和△DEN中，
AB=DE，∠B=∠E，BM=EN，
∴ △ABM≅△DENSAS ，
∴ AM=DN ，
即全等三角形对应边上的中线相等.
【考点】
全等三角形的性质与判定
命题与定理
全等三角形的性质
【解析】
证明：∵ △ABC≅△DEE ，∴ AB=DE,∠B=∠B,BC=EF，
∵ AM，DN分别是BC和EF边上的中线，
∴ BM=12BC,EN=12EF ，∴ BM=FE，
在△ABM和△DEN中， AB=DE∠B=∠EBM=EN，
∴ △ABM≅△DENSAS ，∴ AM=DN .
【解答】
证明：如图：
∵ △ABC≅△DEF ，
∴ AB=DE，∠B=∠E，BC=EF.
∵ AM，DN分别是BC和EF边上的中线，
∴ BM=12BC，EN=12EF ，
∴ BM=EN.
在△ABM和△DEN中，
AB=DE，∠B=∠E，BM=EN，
∴ △ABM≅△DENSAS ，
∴ AM=DN ，
即全等三角形对应边上的中线相等.
【答案】
证明：∵ DE⊥AC，BF⊥AC，
∴ ∠DEC=∠BFA=90∘．
∵ AE=CF，
∴ AE+EF=CF+EF，即AF=CE.
在Rt△ABF和Rt△CDE中，
AB=CD,AF=CE,
∴ Rt△ABF≅Rt△CDE(HL)，
∴ ∠A=∠C，
∴ AB//CD.
【考点】
直角三角形全等的判定
平行线的判定
【解析】
此题暂无解析
【解答】
证明：∵ DE⊥AC，BF⊥AC，
∴ ∠DEC=∠BFA=90∘．
∵ AE=CF，
∴ AE+EF=CF+EF，即AF=CE.
在Rt△ABF和Rt△CDE中，
AB=CD,AF=CE,
∴ Rt△ABF≅Rt△CDE(HL)，
∴ ∠A=∠C，
∴ AB//CD.
【答案】
解：设AB=AC=x，则AD=CD=12x，
若AB+AD=24，BC+CD=30，
则：x+12x=24，
∴ x=16，BC=30−12×16=22，
∴ 三边长分别为16，16，22；
若AB+AD=30，BC+CD=24，
则：x+12x=30，
∴ x=20，BC=24−12×20=14，
∴ 三边长分别为20，20，14；
因此，三角形的三边长为16，16，22或20，20，14．
【考点】
三角形的中线
三角形三边关系
【解析】
分两种情况讨论：当AB+AD=30，BC+DC=24或AB+AD=24，BC+DC=30，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为16，16，22或20，20，14．
【解答】
解：设AB=AC=x，则AD=CD=12x，
若AB+AD=24，BC+CD=30，
则：x+12x=24，
∴ x=16，BC=30−12×16=22，
∴ 三边长分别为16，16，22；
若AB+AD=30，BC+CD=24，
则：x+12x=30，
∴ x=20，BC=24−12×20=14，
∴ 三边长分别为20，20，14；
因此，三角形的三边长为16，16，22或20，20，14．
【答案】
解：∵ ∠A=40∘，∠B=72∘，
∴ ∠ACB=180∘−40∘−72∘=68∘.
∵ CE平分∠ACB，
∴ ∠ACE=∠BCE=34∘，
∴ ∠CED=∠A+∠ACE=74∘，
∴ ∠CDE=90∘，DF⊥CE，
∴ ∠CDF+∠ECD=∠ECD+∠CED=90∘，
∴ ∠CDF=74∘．
【考点】
三角形的外角性质
三角形内角和定理
角平分线的定义
【解析】
首先根据三角形的内角和定理求得∠ACB的度数，再根据CE平分∠ACB求得∠ACE的度数，则根据三角形的外角的性质就可求得∠CED=∠A+∠ACE，再结合CD⊥AB，DF⊥CE就可求解．
【解答】
解：∵ ∠A=40∘，∠B=72∘，
∴ ∠ACB=180∘−40∘−72∘=68∘.
∵ CE平分∠ACB，
∴ ∠ACE=∠BCE=34∘，
∴ ∠CED=∠A+∠ACE=74∘，
∴ ∠CDE=90∘，DF⊥CE，
∴ ∠CDF+∠ECD=∠ECD+∠CED=90∘，
∴ ∠CDF=74∘．
【答案】
解：这种做法合理．理由：
在△BDE和△CFG中，
BE=CG，BD=CF，DE=FG，
∴ △BDE≅△CFG(SSS)，
∴ ∠B=∠C．
【考点】
全等三角形的性质与判定
【解析】
给出的三组相等线段都分布在△BDE，△CFG中，判断他们全等，条件充分，利用全等的性质容易得出∠B=∠C．
【解答】
解：这种做法合理．理由：
在△BDE和△CFG中，
BE=CG，BD=CF，DE=FG，
∴ △BDE≅△CFG(SSS)，
∴ ∠B=∠C．
【答案】
(1)证明：如图，过O作OE⊥AD于E.
∵ ∠B=90∘，
∴ OB⊥AB.
∵ OE⊥AD，OA平分∠BAD，
∴ OB=OE.
∵ 点O是BC的中点，
∴ OB=OC，
∴ OC=OE.
又∵ ∠C=90∘，OC⊥DC，OE⊥AD，
∴ OD平分∠ADC .
(2)解：由(1)知∠B=∠AEO=90∘，
在Rt△ABO和Rt△AEO中，
OB=OE，OA=OA，
∴ Rt△ABO≅△AEOHL，
∴ AB=AE，
同理可证：Rt△DCO≅Rt△DEO，
∴ CD=DE.
∵ AE+DE=AD，
∴AB+CD=AD .
【考点】
角平分线性质定理的逆定理
全等三角形的性质与判定
角平分线的性质
【解析】


【解答】
(1)证明：如图，过O作OE⊥AD于E.
∵ ∠B=90∘，
∴ OB⊥AB.
∵ OE⊥AD，OA平分∠BAD，
∴ OB=OE.
∵ 点O是BC的中点，
∴ OB=OC，
∴ OC=OE.
又∵ ∠C=90∘，OC⊥DC，OE⊥AD，
∴ OD平分∠ADC .
(2)解：由(1)知∠B=∠AEO=90∘，
在Rt△ABO和Rt△AEO中，
OB=OE，OA=OA，
∴ Rt△ABO≅△AEOHL，
∴ AB=AE，
同理可证：Rt△DCO≅Rt△DEO，
∴ CD=DE.
∵ AE+DE=AD，
∴AB+CD=AD .
【答案】
解：(1)根据题意得：
2a+b+4=0，a−b+8=0，
解得：a=−4，b=4.
∴A(−4,0)，B(4,0)．
(2)如图所示，
∵AD⊥BC，
∴∠ADC=90∘，
∴∠1+∠2=90∘.
∵∠BOC=90∘，
∴∠2+∠3=90∘，
∴∠1=∠3，
∵A(−4,0)，B(4,0)，
∴OA=OB.
在△AEO和△BCO中，
∠1=∠3，OA=OB，∠AOE=∠BOC，
∴△AEO≅△BCO(ASA)，
∴OC=OE.
∵C点坐标为(2,0)，
∴OE=OC=2，
∴E点坐标为(0,2)．
(3)∠ADO的度数不发生变化．
如图，过O作OM⊥AD，ON⊥BC，
则∠AMO=∠BNO=90∘.
在△AMO和△BNO中，
∠1=∠3，∠AMO=∠BNO，OA=OB，
∴△AMO≅△BNO(AAS)，
∴OM=ON，
∴DO平分∠ADC.
∵∠ADC=90∘，
∴∠ADO=12∠ADC=45∘．
【考点】
动点问题
全等三角形的性质与判定
角平分线的性质
二元一次方程组的解
坐标与图形性质
角平分线的定义
【解析】



【解答】
解：(1)根据题意得：
2a+b+4=0，a−b+8=0，
解得：a=−4，b=4.
∴A(−4,0)，B(4,0)．
(2)如图所示，
∵AD⊥BC，
∴∠ADC=90∘，
∴∠1+∠2=90∘.
∵∠BOC=90∘，
∴∠2+∠3=90∘，
∴∠1=∠3，
∵A(−4,0)，B(4,0)，
∴OA=OB.
在△AEO和△BCO中，
∠1=∠3，OA=OB，∠AOE=∠BOC，
∴△AEO≅△BCO(ASA)，
∴OC=OE.
∵C点坐标为(2,0)，
∴OE=OC=2，
∴E点坐标为(0,2)．
(3)∠ADO的度数不发生变化．
如图，过O作OM⊥AD，ON⊥BC，
则∠AMO=∠BNO=90∘.
在△AMO和△BNO中，
∠1=∠3，∠AMO=∠BNO，OA=OB，
∴△AMO≅△BNO(AAS)，
∴OM=ON，
∴DO平分∠ADC.
∵∠ADC=90∘，
∴∠ADO=12∠ADC=45∘．