




高中人教版新课标A第一章 三角函数1.1 任意角和弧度制优秀课件ppt
展开在花样滑冰比赛中,运动员的动作是那么优美!尤其是原地转身和空中翻转动作都让我们叹为观止.运动员在原地转身的动作中,仅仅几秒内就能旋转十几圈,甚至二十几圈,因此,花样滑冰美丽而危险.你能算出他们在一次原地转身三圈的动作中转过的角度吗?
1.任意角的概念(1)角的概念角可以看成平面内一条射线绕着________从一个位置旋转到另一个位置所成的图形。
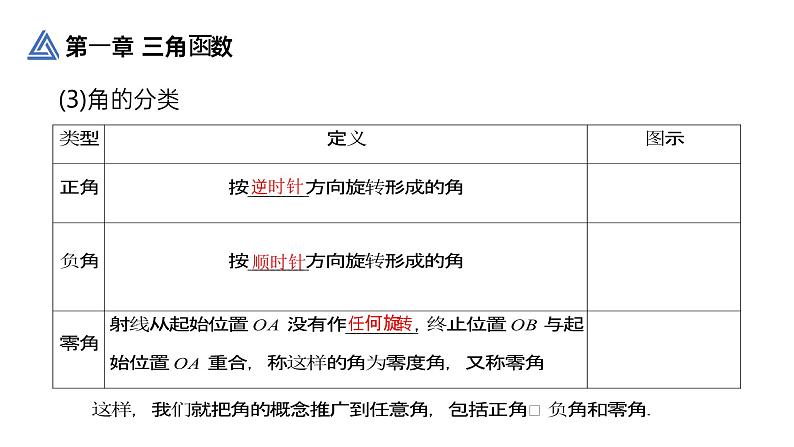
(2)角的表示如图所示:①始边:射线的起始位置OA.②终边:射线的终止位置OB.③顶点:射线的端点O.④记法:图中的角α可记为“角α”或“∠α”或“∠AOB”.
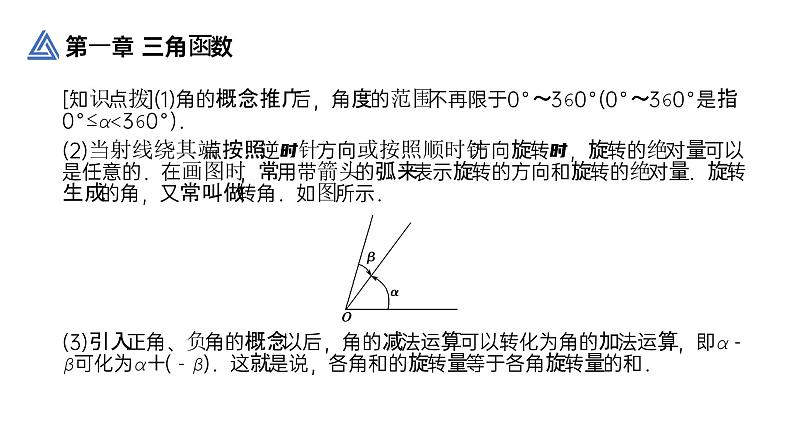
[知识点拨](1)角的概念推广后,角度的范围不再限于0°~360°(0°~360°是指0°≤α<360°).(2)当射线绕其端点按照逆时针方向或按照顺时针方向旋转时,旋转的绝对量可以是任意的.在画图时,常用带箭头的弧来表示旋转的方向和旋转的绝对量.旋转生成的角,又常叫做转角.如图所示.(3)引入正角、负角的概念以后,角的减法运算可以转化为角的加法运算,即α-β可化为α+(-β).这就是说,各角和的旋转量等于各角旋转量的和.
2.象限角与轴线角使角的顶点与________重合,角的始边与______轴的非负半轴重合.那么,角的________(除原点外)在第几象限,就说这个角是第几__________,即象限角的终边在第一或第二或第三或第四象限内,不与__________重合.如果角的终边在坐标轴上,就说这个角不属于任何象限,称为轴线角(象限界角).
[知识点拨] 锐角是第一象限角吗?第一象限角是锐角吗?小于90°的角与它们有什么联系?(1)由锐角的范围知锐角是第一象限角.(2)第一象限的角不一定是锐角,满足{α|k·360°<α
[知识点拨]理解集合S={β|β=α+k·360°,k∈Z}要注意以下几点:(1)式中角α为任意角;(2)k∈Z这一条件必不可少;(3)k·360°与α之间是“+”,如k·360°-30°应看成k·360°+(-30°),即与-30°角终边相同;(4)当角的始边相同时,相等的角的终边一定相同,而终边相同的角不一定相等,终边相同的角有无数个,它们相差360°的整数倍,终边不同则表示的角一定不同.
[拓展]象限角与轴线角(终边在坐标轴上的角)的集合表示(1)象限角:
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.(1)第一象限的角都是锐角.( )(2)终边相同的角一定相等.( )(3)第四象限角可以是负角.( )(4)三角形的内角必是第一、二象限的角.( )(5)-435°是第三象限角.( )
2.将射线OM绕端点O按逆时针方向旋转120°所得的角为( )A.120° B.-120° C.60° D. 240°3.(2018·济南外国语期中)下列各角中,与-1110°的角终边相同的角是( )A.60° B.-60°C.30° D.-30°[解析] -1110°=-3×360°-30°,所以与-30°的角终边相同.
4.若-30°角的始边与x轴的非负半轴重合,现将-30°角的终边按逆时针方向旋转2周,则所得角是____________.[解析] 因为逆时针方向旋转为正角,所以α=-30°+2×360°=690°.
如图(1)(2),射线OA绕端点O旋转到OB,OB1,OB2位置所成的角α=____________,β=______________,γ=__________.
[思路分析] 1.明确角的始边与终边. 2.明确逆时针还是顺时针.[解析] 图(1)中,OA旋转到OB所成的角是一个正角,α=360°+30°=390°.图(2)中,OA旋转到OB1,OB2所成的角分别是一个负角和一个正角,β=-(360°-210°)=-150°,γ=210°-150°=60°.
〔跟踪练习1〕如图,射线OA绕顶点O逆时针旋转45°到OB位置,并在此基础上顺时针旋转120°到达OC位置,则∠AOC=____________.[解析] 由角的定义可得∠AOC=∠AOB+∠BOC=45°+(-120°)=-75°.
已知角α=2 020°.(1)把α改写成k·360°+β(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角;(2)求θ,使θ与α终边相同,且-360°≤θ<720°.[思路分析] 先求出β,判断角α所在的象限;用终边相同的角表示θ满足的不等关系,求出k和θ.
命题方向2 ⇨终边相同的角
『规律总结』 1.把任意角化为α+k·360°(k∈Z,且0°≤α<360°)的形式,关键是确定k,可以用观察法(α的绝对值较小),也可用除法.2.要求适合某种条件且与已知角终边相同的角时,其方法是先求出与已知角终边相同的角的一般形式,再依条件构建不等式求出k的值.
〔跟踪练习2〕若将例题中“角α=2 020°”改为“α=-315°”,其他条件不变,结果如何?
写出终边在如图所示的直线上的角的集合.[思路分析] 首先确定0°~360°范围内终边在所给直线上的两个角,然后分别写出与两个角终边相同的角的集合,最后写出两个集合的并集即可。
命题方向3 ⇨终边在某条直线上的角的集合
[解析] (1)在0°~360°范围内,终边在直线y=0上的角有两个,即0°和180°,又所有与0°角终边相同的角的集合为S1={β|β=0°+k·360°,k∈Z},所有与180°角终边相同的角的集合为S2={β|β=180°+k·360°,k∈Z},于是,终边在直线y=0上的角的集合为S=S1∪S2={β|β=k·180°,k∈Z}.(2)由图形易知,在0°~360°范围内,终边在直线y=-x上的角有两个,即135°和315°,因此,终边在直线y=-x上的角的集合为S={β|β=135°+k·360°,k∈Z}∪{β|β=315°+k·360°,k∈Z}={β|β=135°+k·180°,k∈Z}.
(3)由教材例题知终边在直线y=x上的角的集合为{β|β=45°+k·180°,k∈Z},结合(2)知所求角的集合为S={β|β=45°+k·180°,k∈Z}∪{β|β=135°+k·180°,k∈Z}={β|β=45°+2k·90°,k∈Z}∪{β|β=45°+(2k+1)·90°,k∈Z}={β|β=45°+k·90°,k∈Z}.
『规律总结』 求解终边在某条直线上的角的集合的思路(1)若所求角β的终边在某条射线上,则集合的形式为{β|β=k·360°+α,k∈Z}.(2)若所求角β的终边在某条直线上,则集合的形式为{β|β=k·180°+α,k∈Z}.
〔跟踪练习3〕若α=45°+k·180°(k∈Z),则α的终边在第几象限( )A.第一或第三 B.第二或第三C.第二或第四 D.第三或第四[解析] 分k为奇数,偶数讨论角α的终边所在象限.
若角α的终边在下图中阴影所表示的范围内,则α角组成的集合为_____________________________________________.[解析] 在0°~360°范围内,终边落在阴影范围内的角是60°≤α≤150°,故满足条件的角的集合为{α|k·360°+60°≤α≤k·360°+150°,k∈Z}.
命题方向4 ⇨区域角的表示
{α|k·360°+60°≤α≤k·360°+150°,k∈Z}
『规律总结』 区域角是指终边落在坐标系的某个区域内的角.其写法可分为三步:(1)先按逆时针的方向找到区域的起始和终止边界.(2)按由小到大分别标出起始和终止边界对应的-360°到360°范围内的角α和β,写出最简区间{x|α
分角、倍角所在角限的判断
[解析] ∵α是第一象限角,∴k·360°<α
对任意角的概念不清导致角的范围写错
[错解] 错解一:终边为OA的角为k·360°+30°(k∈Z),终边为OB的角为k·360°+150°(k∈Z),所以终边在阴影部分内的角的集合为{α|k·360°+30°<α
〔跟踪练习6〕若角α的终边在如图所示的阴影部分中,试写出其集合.[解析] 以OA为终边的角为75°+k·360°(k∈Z),以OB边终边的角为k·360°-30°(k∈Z).因此终边落在阴影部分中的角的集合可以表示为{α|k·360°-30°<α
2.-215°是( )A.第一象限角 B.第二象限角C.第三象限角D.第四象限角[解析] 由于-215°=-360°+145°,而145°是第二象限角,则-215°也是第二象限角.3.下列各组角中,终边相同的是( )A.390°,690°B.-330°,750°C.480°,-420°D.3 000°,-840°
4.如图所示,终边落在阴影部分的角的集合是( )A.{α|-45°≤α≤120°}B.{α|120°≤α≤315°}C.{α|k·360°-45°≤α≤k·360°+120°,k∈Z}D.{α|k·360°+120°≤α≤k·360°+315°,k∈Z}
5.若角α与β的终边互为反向延长线,则有( )A.α=β+180°B.α=β-180°C.α=-βD.α=β+(2k+1)·180°,k∈Z[解析] 角α与β的终边互为反向延长线,则α=β+180°+k·360°=β+(2k+1)180°,故选D.
高中数学湘教版(2019)必修 第一册第5章 三角函数5.2 任意角的三角函数一等奖课件ppt: 这是一份高中数学湘教版(2019)必修 第一册第5章 三角函数5.2 任意角的三角函数一等奖课件ppt,共20页。PPT课件主要包含了学习目标,新知学习,即时巩固,随堂小测,课堂小结等内容,欢迎下载使用。
第四章 4.1 任意角、弧度制及任意角的三角函数ppt: 这是一份第四章 4.1 任意角、弧度制及任意角的三角函数ppt,共54页。PPT课件主要包含了一条射线,x轴的非负半轴,α·r等内容,欢迎下载使用。
高中数学人教版新课标A必修41.1 任意角和弧度制课文配套ppt课件: 这是一份高中数学人教版新课标A必修41.1 任意角和弧度制课文配套ppt课件,共19页。PPT课件主要包含了角的概念的推广,任意角,练习P5,象限角,SS1∪S2,{偶数}∪{奇数},={整数}等内容,欢迎下载使用。













