2019-2020学年某校初二（上）10月月考数学试卷

这是一份2019-2020学年某校初二（上）10月月考数学试卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 下列长度的三条线段能组成三角形的是( )
A.1，2，3B.4，5，10C.8，15，20D.5，8，15

2. 如图，小聪把一块含有60∘角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=25∘，则∠2的度数是( )

A.15∘B.25∘C.35∘D.45∘

3. 等腰三角形的一边长为3，周长为19，则该三角形的腰长为( )
A.3B.8C.3或8D.以上均不对

4.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带( )
A.第1块B.第2块C.第3块D.第4块

5. 如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≅△CDN的是( )

A.∠M=∠NB.AM // CNC.AB=CDD.AM=CN

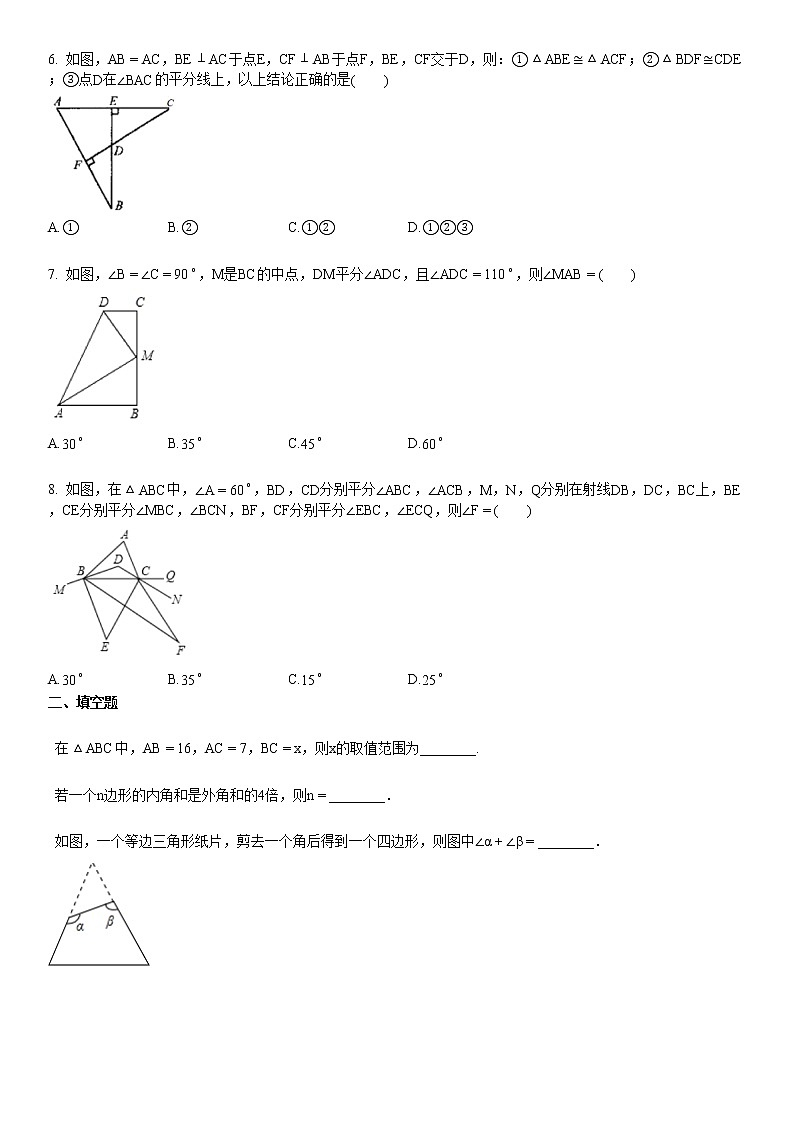
6. 如图，AB=AC，BE⊥AC于点E，CF⊥AB于点F，BE，CF交于D，则：①△ABE≅△ACF；②△BDF≅CDE；③点D在∠BAC的平分线上，以上结论正确的是( )

A.①B.②C.①②D.①②③

7. 如图，∠B=∠C=90∘，M是BC的中点，DM平分∠ADC，且∠ADC=110∘，则∠MAB=( )

A.30∘B.35∘C.45∘D.60∘

8. 如图，在△ABC中，∠A=60∘，BD，CD分别平分∠ABC，∠ACB，M，N，Q分别在射线DB，DC，BC上，BE，CE分别平分∠MBC，∠BCN，BF，CF分别平分∠EBC，∠ECQ，则∠F=( )

A.30∘B.35∘C.15∘D.25∘
二、填空题

在△ABC中，AB=16，AC=7，BC=x，则x的取值范围为________.

若一个n边形的内角和是外角和的4倍，则n=________．

如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β=________．


如图，已知AF=DE，∠A=∠D，请你添一个直接条件，________，使△AFC≅△DEB．


如图在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且△ABC的面积是4，则△BEF的面积是________．


如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是________．


如图，动点P从(0, 3)出发，沿所示方向运动，每当碰到长方形OABC的边时反弹，反弹后的路径与长方形的边的夹角为45∘，第1次碰到长方形边上的点的坐标为(3, 0)，则第2019次碰到长方形边上的点的坐标为________．


如图，任意画一个∠BAC=60∘的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD交于点P，连结AP．有以下结论：①AP平分∠BAC；②PD=PE；③BD+CE=BC；④S△PBD+S△PCE=S△PBC.
其中正确的序号是________(填序号).

三、解答题


如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35∘，∠D=42∘，求∠ACD的度数．


如图，CE=CB，CD=CA，∠DCA=∠ECB，求证：DE=AB．

如图所示，已知∠1=∠2，请你添加一个条件，证明：AB=AC．

(1)你添加的条件是________；

(2)请写出证明过程．

已知，如图所示，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．


如图，∠ACB=90∘，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD=2.5cm，DE=1.7cm．

(1)证明：△ACD≅△CBE；

(2)求BE的长．

在△ABC中，∠ABC=∠C，D是BA延长线上的一点，E是AC的中点．

(1)实践与操作：利用尺规按下列要求作图，并在图中标明相应字母(保留作图痕迹，不写作法).
①作∠DAC的平分线AM；
②连结BE并延长交AM于点F；

(2)猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由．

探究与发现：
如图1所示的图形，像我们常见的学习用品——圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：

1观察“规形图”，试探究∠BDC与∠A，∠B，∠C之间的关系，并说明理由；

2请你直接利用以上结论，解决以下三个问题：
①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY，XZ恰好经过点B，C，若∠A=50∘，则∠ABX+∠ACX=________​∘；
②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=50∘，∠DBE=130∘，求∠DCE=________​∘；
③如图4，∠ABD，∠ACD的10等分线相交于点G1，G2…，G9，若∠BDC=140∘，∠BG1C=77∘，求∠A的度数．

如图，已知：Rt△ABC和Rt△DBE，∠ABC=∠DBE=90∘，AB=CB，DB=EB，延长CE交AD于点F．

(1)如图1，点D在△ABC外，点E在AB边上时，求证：AD=CE，AD⊥CE；

(2)若将(1)中的△DBE绕点B顺时针旋转，使点E在△ABC的内部，CF交AB于点O，如图2，则(1)中的结论是否仍然成立？请证明；

(3)若将(1)中的△DBE绕点B顺时针旋转，使点E在△ABC的外部，如图3，请直接写出AD，CE的数量关系及位置关系.
参考答案与试题解析
2019-2020学年湖北省通山县某校初二（上）10月月考数学试卷
一、选择题
1.
【答案】
C
【考点】
三角形三边关系
【解析】
根据三角形的三边关系进行分析判断．
【解答】
解：根据三角形任意两边的和大于第三边，得
A中，1+2=3，不能组成三角形；
B中，5+4=9<10，不能组成三角形；
C中，8+15>20，能够组成三角形；
D中，5+8=13<15，不能组成三角形．
故选C.
2.
【答案】
C
【考点】
平行线的性质
【解析】
先根据两直线平行，内错角相等求出∠3，再根据直角三角形的性质用∠2=60∘−∠3代入数据进行计算即可得解．
【解答】
解：如图所示：
∵ 直尺的两边互相平行，∠1=25∘，
∴ ∠3=∠1=25∘，
∴ ∠2=60∘−∠3=60∘−25∘=35∘．
故选C．
3.
【答案】
B
【考点】
三角形三边关系
等腰三角形的性质
【解析】
此题要分情况考虑：3cm是底或3cm是腰．根据周长求得另一边，再进一步根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，判断是否能够组成三角形．
【解答】
解：当3是底时，则腰长是(19−3)÷2=8，此时能够组成三角形；
当3是腰时，则底是19−3×2=13，此时3+3<13，不能组成三角形，应舍去．
故选B．
4.
【答案】
B
【考点】
全等三角形的应用
【解析】
本题应先假定选择哪块，再对应三角形全等判定的条件进行验证．
【解答】
解：1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，
只有第2块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的．
故选B.
5.
【答案】
D
【考点】
全等三角形的判定
【解析】
根据三角形全等的判定定理，有AAS、SSS、ASA、SAS四种．逐条验证即可．
【解答】
解：A，∠M=∠N，符合ASA，能判定△ABM≅△CDN，故A选项不符合题意；
B，AM // CN，得出∠MAB=∠NCD，符合AAS，能判定△ABM≅△CDN，故B选项不符合题意；
C，AB=CD，符合SAS，能判定△ABM≅△CDN，故C选项不符合题意；
D，根据条件AM=CN，MB=ND，∠MBA=∠NDC，不能判定△ABM≅△CDN，故D选项符合题意.
故选D．
6.
【答案】
D
【考点】
全等三角形的性质与判定
角平分线的性质
【解析】
连接AD．由△ABE≅△ACF，故①正确，推出AE=AF，由AB=AC，推出EC=BF，推出△DEC≅△DFB，故②正确，推出DE=DF，由DE⊥AC，DF⊥AB，推出DA平分∠CAB，故③正确．
【解答】
解：∵ BE⊥AC于点E，CF⊥AB于点F，
∴ ∠AEB=∠AFC=90∘，∠DEC=∠DFB=90∘，
在△ABE和△ACF中，
∠BAE=∠CAF,∠AEB=∠AFC,AB=AC,
∴ △ABE≅△ACF(AAS)，故①正确；
∴ AE=AF，
∵ AB=AC，
∴ EC=BF，
在△CDE和△BDF中，
∠EDC=∠FDB,∠DEC=∠DFB,EC=FB,
∴ △CDE≅△BDF(AAS)，故②正确；
∴ DE=DF，
如图，连接AD．
∵ DE⊥AC，DF⊥AB，
∴ DA平分∠CAB，即点D在∠BAC的平分线上，故③正确.
故选D．
7.
【答案】
B
【考点】
角平分线的性质
【解析】
作MN⊥AD于N，根据平行线的性质求出∠DAB，根据角平分线的判定定理得到∠MAB=12∠DAB，计算即可．
【解答】
解：作MN⊥AD于N，如图，
∵ ∠B=∠C=90∘，
∴ AB // CD，
∴ ∠DAB=180∘−∠ADC=70∘，
∵ DM平分∠ADC，MN⊥AD，MC⊥CD，
∴ MN=MC，
∵ M是BC的中点，
∴ MC=MB，
∴ MN=MB，又MN⊥AD，MB⊥AB，
∴ ∠MAB=12∠DAB=35∘.
故选B.
8.
【答案】
C
【考点】
三角形的外角性质
三角形内角和定理
角平分线的性质
【解析】
先由BD、CD分别平分∠ABC、∠ACB得到∠DBC=12∠ABC，∠DCB=12∠ACB，在△ABC中根据三角形内角和定理得∠DBC+∠DCB=12(∠ABC+∠ACB)=12(180∘−∠A)=60∘，则根据平角定理得到∠MBC+∠NCB=300∘；再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6=12∠MBC，∠1=12∠NCB，两式相加得到∠5+∠6+∠1=12(∠NCB+∠NCB)=150∘，在△BCE中，根据三角形内角和定理可计算出∠E=30∘；再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6，∠2=∠3+∠4，根据三角形外角性质得到∠3+∠4=∠5+∠F，∠2+∠3+∠4=∠5+∠6+∠E，利用等量代换得到∠2=∠5+∠F，2∠2=2∠5+∠E，再进行等量代换可得到∠F=12∠E．
【解答】
解：如图所示：
∵ BD，CD分别平分∠ABC，∠ACB，∠A=60∘，
∴ ∠DBC=12∠ABC，∠DCB=12∠ACB，
∴ ∠DBC+∠DCB=12(∠ABC+∠ACB)=12(180∘−∠A)
=12(180∘−∠A)=12×(180∘−60∘)=60∘，
∴ ∠MBC+∠NCB=360∘−60∘=300∘.
∵ BE，CE分别平分∠MBC，∠BCN，
∴ ∠5+∠6=12∠MBC，∠1=12∠NCB，
∴ ∠5+∠6+∠1=12(∠NCB+∠NCB)=150∘，
∴ ∠E=180∘−(∠5+∠6+∠1)=180∘−150∘=30∘.
∵ BF，CF分别平分∠EBC，∠ECQ，
∴ ∠5=∠6，∠2=∠3+∠4，
∵ ∠3+∠4=∠5+∠F，∠2+∠3+∠4=∠5+∠6+∠E，
即∠2=∠5+∠F，2∠2=2∠5+∠E，
∴ 2∠F=∠E，
∴ ∠F=12∠E=12×30∘=15∘．
故选C．
二、填空题
【答案】
9【考点】
三角形三边关系
【解析】
根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析求解．
【解答】
解：根据三角形的三边关系，得
16−7故答案为：9【答案】
10
【考点】
多边形内角与外角
【解析】
利用多边形的外角和以及多边形的内角和定理即可解决问题．
【解答】
解：∵ 多边形的外角和是360∘，多边形的内角和是外角和的4倍，
∴ 内角和是1440∘，
根据多边形的内角和为(n−2)×180∘=1440∘，
则n=10.
故答案为：10.
【答案】
240∘
【考点】
多边形内角与外角
等边三角形的性质
【解析】
本题可先根据等边三角形顶角的度数求出两底角的度数和，然后在四边形中根据四边形的内角和为360∘，求出∠α+∠β的度数．
【解答】
解：∵ 等边三角形的顶角为60∘，
∴ 两底角和=180∘−60∘=120∘.
∴ ∠α+∠β=360∘−120∘=240∘.
故答案为：240∘．
【答案】
AC=DB
【考点】
全等三角形的判定
【解析】
有已知可得两三角形有一组对应角相等，一组对应边相等，然后根据全等三角形的判定方法的不同对各选项分析判断后利用排除法求解．
【解答】
解：添加的条件为：AC=DB.
∵ 在△AFC和△DEB中，
AF=DE,∠A=∠D,AC=DB,
∴ △AFC≅△DEB(SAS)．
故答案为：AC=DB.
【答案】
1
【考点】
三角形的面积
【解析】
依据三角形的面积公式及点D、E、F分别为边BC，AD，CE的中点，推出S△BEF=14S△ABC，从而求得△BEF的面积．
【解答】
解：∵ 点D，E，F分别为边BC，AD，CE的中点，
∴ S△ABD=12S△ABC，S△BDE=12S△ABD，
S△CDE=12S△ADC，S△BEF=12S△BEC，
∴ S△BEF=14S△ABC.
∵ △ABC的面积是4，
∴ S△BEF=1．
故答案为：1.
【答案】
60∘
【考点】
全等三角形的性质
【解析】
根据题目已知条件可证△ABD≅△BCE，再利用全等三角形的性质及三角形外角和定理求解．
【解答】
解：∵ 等边△ABC，
∴ ∠ABD=∠C，AB=BC，
在△ABD与△BCE中，AB=BC，∠ABD=∠C，BD=CE，
∴ △ABD≅△BCE(SAS)，
∴ ∠BAD=∠CBE，
∵ ∠ABE+∠EBC=60∘，
∴ ∠ABE+∠BAD=60∘，
∴ ∠APE=∠ABE+∠BAD=60∘，
∴ ∠APE=60∘．
故答案为：60∘．
【答案】
(8, 3)
【考点】
规律型：点的坐标
【解析】
根据图形可以直接写出第3次碰到长方形边上的点的坐标，然后再根据题意画出图形观察规律，从而可以得出2015次碰到长方形边上的点的坐标．
【解答】
解：根据题意，如下图示：
通过上图观察可知，每碰撞6次回到始点．
∵ 2019÷6=，
根据图形可知，第3次碰到长方形边上的点的坐标为(8, 3)，
∴ 第2019次碰到长方形边上的点的坐标为(8, 3)．
故答案为：(8, 3)．
【答案】
①②③④
【考点】
角平分线的性质
全等三角形的性质与判定
【解析】
由于BE、CD分别是∠ABC与∠ACB的角平分线，∠BAC=60∘可得出∠PBC+∠PCB的度数，再由三角形内角和定理可求出∠BPC的度数；由∠BPC=120∘可知∠DPE=120∘，过点P作PF⊥AB，PG⊥AC，PH⊥BC，由角平分线的性质可知AP是∠BAC的平分线，PF=PG=PH，故∠AFP=∠AGP=90∘，由四边形内角和定理可得出∠FPG=120∘，故∠DPF=∠EPG，由全等三角形的判定定理可得出△PFD≅△PGE，故可得出PD=PE；由三角形全等的判定定理可得出△BHP≅△BFP，△CHP≅△CGP，故可得出BH=BD+DF，CH=CE−GE，再由DF=EG可得出BC=BD+CE，故可得出S△PBD+S△PCE=S△PBC；由AP是∠BAC的平分线可用AP表示出AF及AG的长，再根据DF=EG即可得出AD+AE=3AP．
【解答】
解：过点P作PF⊥AB，PG⊥AC，PH⊥BC，
∵ BE，CD分别是∠ABC与∠ACB的角平分线，
∴ AP是∠BAC的平分线，PF=PG=PH. 故①正确；
∵ BE，CD分别是∠ABC与∠ACB的角平分线，∠BAC=60∘，
∴ ∠PBC+∠PCB=12(180∘−∠BAC)=12(180∘−60∘)=60∘，
∴ ∠BPC=180∘−(∠PBC+∠PCB)=180∘−60∘=120∘，
∵ ∠BPC=120∘，
∴ ∠DPE=120∘，
∵ ∠BAC=60∘，∠AFP=∠AGP=90∘，
∴ ∠FPG=120∘，
∴ ∠DPF=∠EPG，
在△PFD与△PGE中，
∵ ∠DFP=∠EGP=90∘,PF=PG,∠DPF=∠EPG,
∴ △PFD≅△PGE(ASA)，
∴ PD=PE，故②正确；
在Rt△BHP与Rt△BFP中，
∵ PF=PH,BP=BP,
∴ Rt△BHP≅Rt△BFP(HL)，
同理，Rt△CHP≅Rt△CGP，
∴ BH=BD+DF①，CH=CE−GE②，
两式相加得，BH+CH=BD+DF+CE−GE，
∵ DF=EG，
∴ BC=BD+CE，故③正确；
∵ PF=PG=PH，
∴ S△PBD+S△PCE=S△PBC，故④正确.
故答案为：①②③④.
三、解答题
【答案】
解：∵ ∠AFE=90∘，
∴ ∠AEF=90∘−∠A=90∘−35∘=55∘，
∴ ∠CED=∠AEF=55∘，
∴ ∠ACD=180∘−∠CED−∠D
=180∘−55∘−42∘=83∘．
【考点】
三角形内角和定理
【解析】
根据三角形外角与内角的关系及三角形内角和定理解答．
【解答】
解：∵ ∠AFE=90∘，
∴ ∠AEF=90∘−∠A=90∘−35∘=55∘，
∴ ∠CED=∠AEF=55∘，
∴ ∠ACD=180∘−∠CED−∠D
=180∘−55∘−42∘=83∘．
【答案】
证明：∵ ∠DCA=∠ECB，
∴ ∠DCA+∠ACE=∠BCE+∠ACE，
∴ ∠DCE=∠ACB，
∵ 在△DCE和△ACB中
DC=AC∠DCE=∠ACBCE=CB，
∴ △DCE≅△ACB，
∴ DE=AB．
【考点】
全等三角形的性质与判定
【解析】
求出∠DCE=∠ACB，根据SAS证△DCE≅△ACB，根据全等三角形的性质即可推出答案．
【解答】
证明：∵ ∠DCA=∠ECB，
∴ ∠DCA+∠ACE=∠BCE+∠ACE，
∴ ∠DCE=∠ACB，
∵ 在△DCE和△ACB中
DC=AC∠DCE=∠ACBCE=CB，
∴ △DCE≅△ACB，
∴ DE=AB．
【答案】
∠B=∠C
(2)证明：在△ABD和△ACD中，
∠B=∠C,∠1=∠2,AD=AD,
∴ △ABD≅△ACD(AAS)，
∴ AB=AC．
【考点】
全等三角形的性质
【解析】
（1）此题是一道开放型的题目，答案不唯一，如∠B=∠C或∠ADB=∠ADC等；
（2）根据全等三角形的判定定理AAS推出△ABD≅△ACD，再根据全等三角形的性质得出即可．
【解答】
(1)解：添加的条件是∠B=∠C，
∵ ∠1=∠2，AD为公共边，再添加∠B=∠C，
∴ △ABD≅△ACD(AAS)，
故答案为：∠B=∠C.
(2)证明：在△ABD和△ACD中，
∠B=∠C,∠1=∠2,AD=AD,
∴ △ABD≅△ACD(AAS)，
∴ AB=AC．
【答案】
证明：连接AD，
在△ACD和△ABD中，
AC=AB,CD=BD,AD=AD,
∴ △ACD≅△ABD(SSS)，
∴ ∠EAD=∠FAD，即AD平分∠EAF，
∵ DE⊥AE，DF⊥AF，
∴ DE=DF．
【考点】
角平分线的性质
全等三角形的性质
【解析】
连接AD，利用SSS得到三角形ABD与三角形ACD全等，利用全等三角形对应角相等得到∠EAD=∠FAD，即AD为角平分线，再由DE⊥AB，DF⊥AC，利用角平分线定理即可得证．
【解答】
证明：连接AD，
在△ACD和△ABD中，
AC=AB,CD=BD,AD=AD,
∴ △ACD≅△ABD(SSS)，
∴ ∠EAD=∠FAD，即AD平分∠EAF，
∵ DE⊥AE，DF⊥AF，
∴ DE=DF．
【答案】
(1)证明：∵ ∠ACB=90∘，BE⊥CE，AD⊥CE，
∴ ∠BEC=∠ACB=∠ADC=90∘，
∴ ∠ACE+∠BCE=90∘，∠BCE+∠CBE=90∘，
∴ ∠ACD=∠CBE，
在△ACD和△CBE中，
∠ADC=∠BEC,∠ACD=∠CBE,AC=BC,
∴ △ACD≅△CBE(AAS)；
(2)解：∵ △ACD≅△CBE，
∴ AD=CE，BE=CD，
∴ BE=CE−DE=AD−DE=2.5−1.7=0.8(cm)．
【考点】
全等三角形的判定
全等三角形的性质
【解析】
（1）根据垂直定义求出∠BEC=∠ACB=∠ADC，根据等式性质求出∠ACD=∠CBE，根据AAS证明△BCE≅△CAD；
（2）根据全等三角形的对应边相等得到AD=CE，BE=CD，利用DE=CE−CD，即可解答．
【解答】
(1)证明：∵ ∠ACB=90∘，BE⊥CE，AD⊥CE，
∴ ∠BEC=∠ACB=∠ADC=90∘，
∴ ∠ACE+∠BCE=90∘，∠BCE+∠CBE=90∘，
∴ ∠ACD=∠CBE，
在△ACD和△CBE中，
∠ADC=∠BEC,∠ACD=∠CBE,AC=BC,
∴ △ACD≅△CBE(AAS)；
(2)解：∵ △ACD≅△CBE，
∴ AD=CE，BE=CD，
∴ BE=CE−DE=AD−DE=2.5−1.7=0.8(cm)．
【答案】
解：(1)如图所示：
(2)AF // BC，且AF=BC，
理由如下：
∵ ∠ABC=∠C，
∴ ∠DAC=∠ABC+∠C=2∠C，
由作图可得∠DAC=2∠FAC，
∴ ∠C=∠FAC，
∴ AF // BC.
∵ E为AC中点，
∴ AE=EC，
在△AEF和△CEB中∠FAE=∠C,AE=CE,∠AEF=∠BEC,
∴ △AEF≅△CEB(ASA)，
∴ AF=BC．
【考点】
全等三角形的性质与判定
作图—复杂作图
【解析】
（1）根据题意画出图形即可；
（2）首先根据等腰三角形的性质与三角形内角与外角的性质证明∠C=∠FAC，进而可得AF // BC；然后再证明△AEF≅△CEB，即可得到AF=BC．
【解答】
解：(1)如图所示：
(2)AF // BC，且AF=BC，
理由如下：
∵ ∠ABC=∠C，
∴ ∠DAC=∠ABC+∠C=2∠C，
由作图可得∠DAC=2∠FAC，
∴ ∠C=∠FAC，
∴ AF // BC.
∵ E为AC中点，
∴ AE=EC，
在△AEF和△CEB中∠FAE=∠C,AE=CE,∠AEF=∠BEC,
∴ △AEF≅△CEB(ASA)，
∴ AF=BC．
【答案】
解：1连接AD并延长至点F，
由外角定理可得∠BDF=∠BAD+∠B，∠CDF=∠C+∠CAD，
且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD，
相加可得∠BDC=∠A+∠B+∠C；
40,90
【考点】
三角形的外角性质
三角形内角和定理
【解析】
（1）根据题意观察图形连接AD并延长至点F，由外角定理可知，一个三角形的外角等于与它不相邻的两个内角的和，则容易得到∠BDC=∠BDF+∠CDF；
（2）①由（1）的结论可得∠ABX+∠ACX+∠A=∠BXC，然后把∠A=50∘，∠BXC=90∘代入上式即可得到∠ABX+∠ACX的值．
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB，代入∠DAE=50∘，∠DBE=130∘即可得到∠ADB+∠AEB的值，再利用上面得出的结论可知∠DCE=12(∠ADB+∠AEB)+∠A，易得答案．
③由（2）的方法，进而可得答案．
【解答】
解：1连接AD并延长至点F，
由外角定理可得∠BDF=∠BAD+∠B，∠CDF=∠C+∠CAD，
且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD，
相加可得∠BDC=∠A+∠B+∠C；
2①由1的结论易得：∠ABX+∠ACX+∠A=∠BXC，
又因为∠A=50∘，∠BXC=90∘，
所以∠ABX+∠ACX=90∘−50∘=40∘，
故答案为：40；
②由1的结论易得∠DBE=∠A+∠ADB+∠AEB，
因为∠DAE=50∘，∠DBE=130∘
所以∠ADB+∠AEB=80∘；
而∠DCE=12(∠ADB+∠AEB)+∠A，
所以∠DCE=90∘，
故答案为：90；
③由②规律得：∠BG1C=110(∠ABD+∠ACD)+∠A，
因为∠BG1C=77∘，
所以设∠A为x∘，
因为∠ABD+∠ACD=140∘−x∘
所以110(140−x)+x=77，
14−110x+x=77，
解得：x=70，
所以∠A为70∘．
【答案】
(1)证明：在△ABD和△CBE中，
AB=CB,∠ABD=∠CBE=90∘,DB=EB,
∴ △ABD≅△CBE(SAS)，
∴ AD=CE，∠BAD=∠BCE.
∵ ∠BCE+∠BEC=90∘，∠AEF=∠BEC，
∴ ∠BAD+∠AEF=90∘，
∴ ∠AFE=90∘，
∴ AD⊥CE.
(2)解：(1)中的结论AD=CE，AD⊥CE仍然成立，理由为：
∵ ∠ABC=∠DBE=90∘，
∴ ∠ABC−∠ABE=∠DBE−∠ABE，即∠ABD=∠CBE，
在△ABD和△CBE中，
AB=CB,∠ABD=∠CBE,DB=EB,
∴ △ABD≅△CBE(SAS)，
∴ AD=CE，∠BAD=∠BCE.
∵ ∠BCE+∠BOC=90∘，∠AOF=∠BOC，
∴ ∠BAD+∠AOF=90∘，
∴ ∠AFE=90∘，
∴ AD⊥CE.
(3)解：AD=CE，AD⊥CE，理由为：
如图，
∵ ∠ABC=∠DBE=90∘，
∴ ∠ABC−∠DBC=∠DBE−∠DBC，即∠ABD=∠CBE，
在△ABD和△CBE中，
AB=CB,∠ABD=∠CBE,DB=EB,
∴ △ABD≅△CBE(SAS)，
∴ AD=CE，∠BAD=∠BCE.
∵ ∠BAD+∠AMB=90∘，∠AMB=∠CMF，
∴ ∠BCE+∠CMF=90∘，
∴ ∠AFC=90∘，
∴ AD⊥CE．
【考点】
全等三角形的性质与判定
旋转的性质
【解析】
(1)由AB=CB，DB=EB，加上夹角为直角相等，利用SAS可得出△ABD≅△CBE，利用全等三角形的对应边相等，对应角相等可得出AD=CE，∠BAD=∠BCE，在直角三角形EBC中，两锐角互余，再由对顶角相等，得到三角形AEF中两个角互余，可得出CF垂直于AD，得证；
(2)(1)中的结论AD=CE，AD⊥CE仍然成立，理由为：由一对直角相等，都减去∠ABE，得到∠ABD=∠CBE，再由AB=BC，DB=EB，利用SAS得出△ABD≅△CBE，同(1)可得出AD=CE，AD⊥CE；
(3)结论为：AD=CE，AD⊥CE，证明方法同上．
【解答】
(1)证明：在△ABD和△CBE中，
AB=CB,∠ABD=∠CBE=90∘,DB=EB,
∴ △ABD≅△CBE(SAS)，
∴ AD=CE，∠BAD=∠BCE.
∵ ∠BCE+∠BEC=90∘，∠AEF=∠BEC，
∴ ∠BAD+∠AEF=90∘，
∴ ∠AFE=90∘，
∴ AD⊥CE.
(2)解：(1)中的结论AD=CE，AD⊥CE仍然成立，理由为：
∵ ∠ABC=∠DBE=90∘，
∴ ∠ABC−∠ABE=∠DBE−∠ABE，即∠ABD=∠CBE，
在△ABD和△CBE中，
AB=CB,∠ABD=∠CBE,DB=EB,
∴ △ABD≅△CBE(SAS)，
∴ AD=CE，∠BAD=∠BCE.
∵ ∠BCE+∠BOC=90∘，∠AOF=∠BOC，
∴ ∠BAD+∠AOF=90∘，
∴ ∠AFE=90∘，
∴ AD⊥CE.
(3)解：AD=CE，AD⊥CE，理由为：
如图，
∵ ∠ABC=∠DBE=90∘，
∴ ∠ABC−∠DBC=∠DBE−∠DBC，即∠ABD=∠CBE，
在△ABD和△CBE中，
AB=CB,∠ABD=∠CBE,DB=EB,
∴ △ABD≅△CBE(SAS)，
∴ AD=CE，∠BAD=∠BCE.
∵ ∠BAD+∠AMB=90∘，∠AMB=∠CMF，
∴ ∠BCE+∠CMF=90∘，
∴ ∠AFC=90∘，
∴ AD⊥CE．