初中数学北师大版八年级下册2 直角三角形多媒体教学课件ppt

这是一份初中数学北师大版八年级下册2 直角三角形多媒体教学课件ppt，共17页。PPT课件主要包含了问题探究，BDCD，强化巩固，不必再证全等，它的逆命题是什么，拓展延伸等内容，欢迎下载使用。

回忆角平分线的性质定理
角的平分线上的点到角的两边的距离相等。
如何证明这个定理?先分析它的条件和结论是什么?
已知：如图，OC是的∠AOB的平分线，点P在OC上， PD⊥OA，PE⊥OB，垂足分别是D，E。
证明：∵ PD⊥OA，PE⊥OB（已知） ∴∠PDO=∠PEO=90°（垂直的定义）
在△PDO和△PEO中
∴ PD=PE（全等三角形的对应边相等）
∠ PDO= ∠ PEO ∠ AOC= ∠ BOC OP=OP
∴ △ PDO≌ △ PEO（AAS）
定理:角的平分线上的点到角的两边的距离相等。
几何符号语言表示∵ OP平分∠AOB且PD⊥OA，PE⊥OB，∴PD=PE
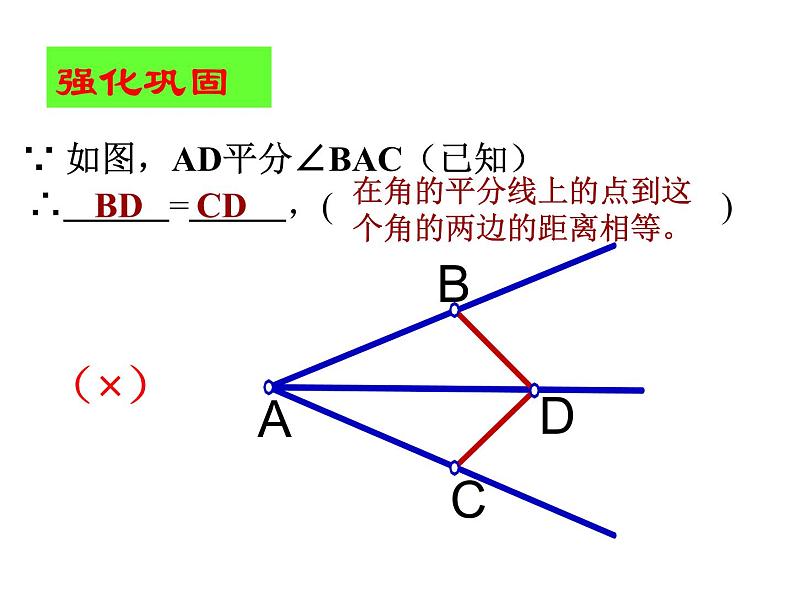
∵ 如图，AD平分∠BAC（已知）
∴ = ，( )
在角的平分线上的点到这个角的两边的距离相等。
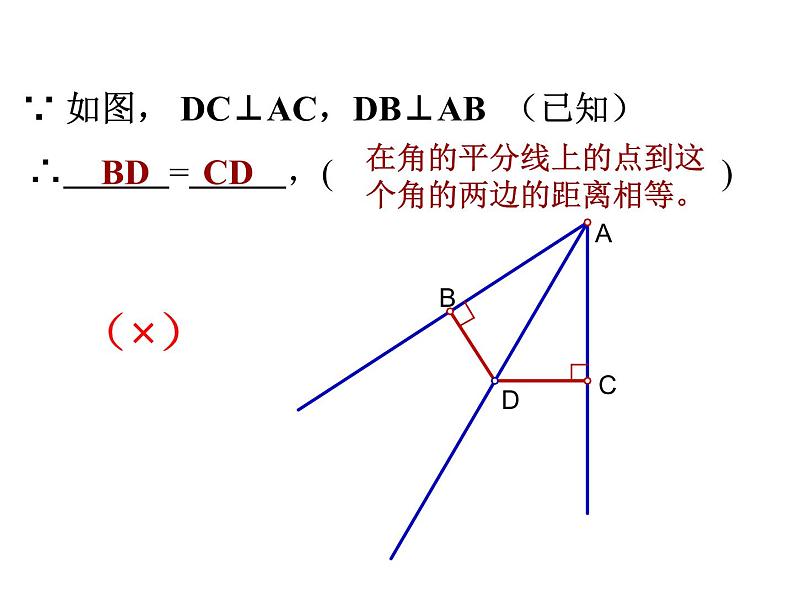
∵ 如图， DC⊥AC，DB⊥AB （已知）
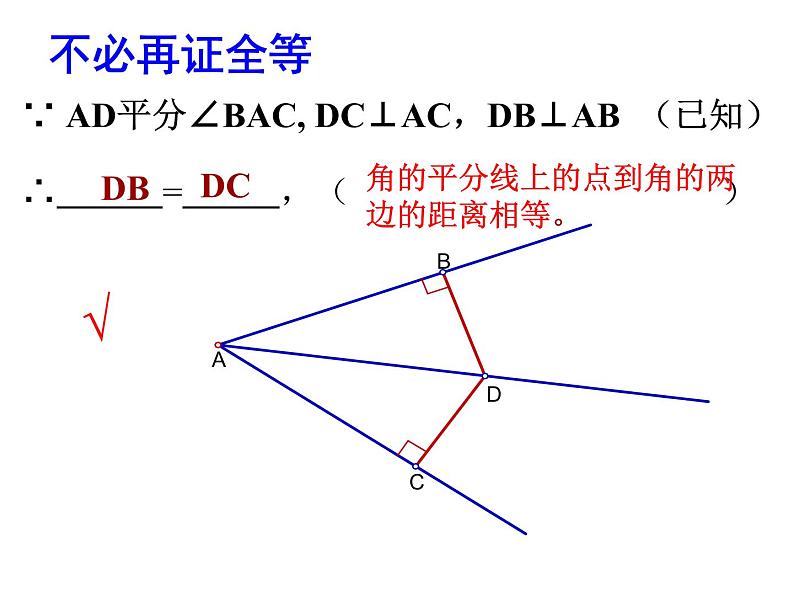
∵ AD平分∠BAC, DC⊥AC，DB⊥AB （已知）
∴ = ，（ ）
角的平分线上的点到角的两边的距离相等。
到角两边距离相等的点在这个角的平分线上。
如何证明这个命题?先分析它的条件和结论是什么?
已知：如图. PD⊥OA于D，PE⊥OB与E， 且PD=PE
求证：点P在∠AOBA的平分线上
证明：连接OP并延长(或作射线OP)
∵ PD⊥OA，PE⊥OB
∴∠ODP=∠OEP=90°
∵在Rt△ODP和Rt△OEP中
命题：到角两边距离相等的点在这个角的平分线上。
∵PD⊥OA，PE⊥OB，且PD=PE∴OP平分∠AOB
OP=OP PD=PE
∴Rt△ODP≌Rt△OEP（HL）
练习：1. 如图，△ABC中，∠C=90°，D 在AC 上，DE⊥AB与E，且 DE=DC，∠CBD=2∠A， 则∠A=＿＿＿＿＿。
2. 如图，在CD上找一点P，使它到OA，OB的距离相等，则P点的位置在哪里？
若要使点P也要到C、D的距离也相等，点P的位置在哪里？
“如果一个点到角的两边的距离不相等，那么这个点不在角平分线上。”
你认为这个结论正确吗？
如果正确，你能证明它吗？
友情提示：假设结论的反面成立，会出现什么状况？
练习：你认为“在一个三角形中，如果两个角不相等，那么这两个角对应的边也不相等”对吗？ 用自己的语言说说看
问题. 如图△ABC的角的平分线BE、CF相交于点O，观察交点O到这个三角形三边的距离，你有哪些发现？你能证明你的发现吗？
结论（1）三角形两角平分线的交点到三边的距离相等。
（2）点O也在∠BAC的角平分线上。
（3）定理：三角形三条角平分线交于一点。
问题. 将上题中的两条内角平分线改为两条外角平分线，这时结论会有变化吗？
已知：如图，在△ABC中，∠C=90度，点D在BC上，DE垂直平分AB，且DE=DC。求∠B的度数
例 已知：如图 DB⊥AB，DC⊥AC，B，C分别为垂足，DB=DC。求证：DA平分∠BDC
∵ DB⊥AB，DC⊥AC， DB=DC
∴∠3=90°－∠1 ∠4=90°－∠2
（到一个角的两边的距离相等的点， 在这个角的平分线上）
（1）角平分线的性质定理及其逆定理及作用；
（2）用这两个定理，一定要具备两个垂直距离（即点到直线的距离），证明过程中要直接应用这两个定理，而不要去寻找全等三角形（这样做实际是重新证了一次定理）。
（3）怎样找三角形内到三角形三边距离相等的点。