初中数学北师大版八年级下册第一章 三角形的证明1 等腰三角形备课ppt课件

这是一份初中数学北师大版八年级下册第一章 三角形的证明1 等腰三角形备课ppt课件，共15页。PPT课件主要包含了本节课学些什么等内容，欢迎下载使用。

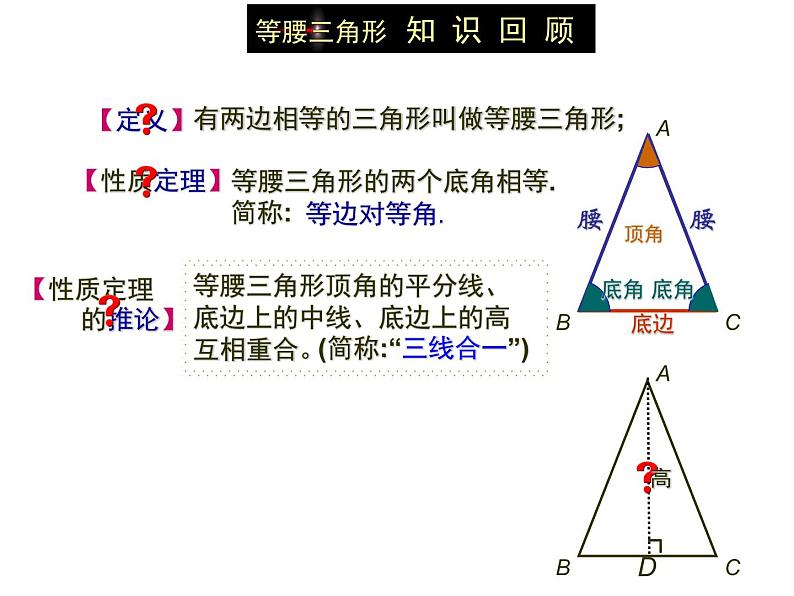
等腰三角形 知 识 回 顾
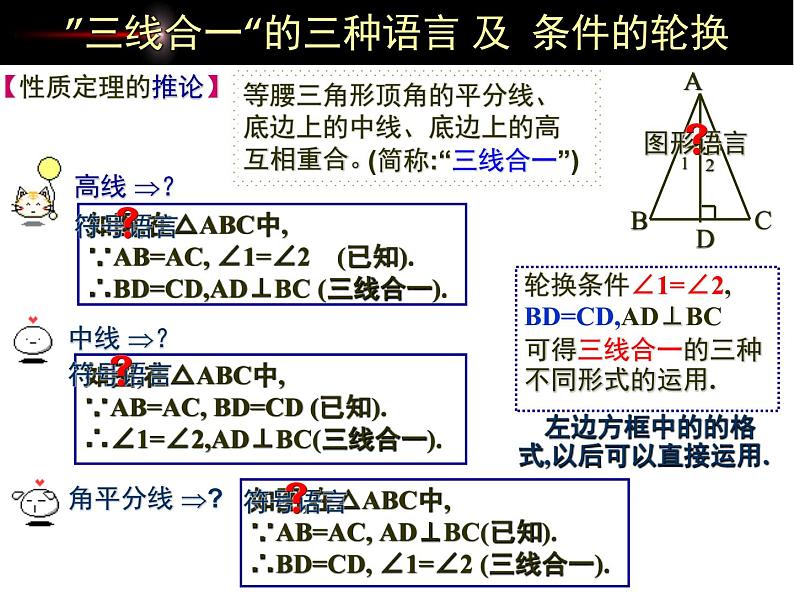
等腰三角形顶角的平分线、底边上的中线、底边上的高 互相重合。
【性质定理 的推论】
有两边相等的三角形叫做等腰三角形;
(简称:“三线合一”)
如图,在△ABC中, ∵AB=AC, ∠1=∠2 (已知).∴BD=CD,AD⊥BC (三线合一).
左边方框中的的格式,以后可以直接运用.
如图,在△ABC中, ∵AB=AC, BD=CD (已知).∴∠1=∠2,AD⊥BC(三线合一).
如图,在△ABC中, ∵AB=AC, AD⊥BC(已知).∴BD=CD, ∠1=∠2 (三线合一).
轮换条件∠1=∠2,BD=CD,AD⊥BC可得三线合一的三种不同形式的运用.
”三线合一“的三种语言 及 条件的轮换
这就是本节课的学习的主要内容。
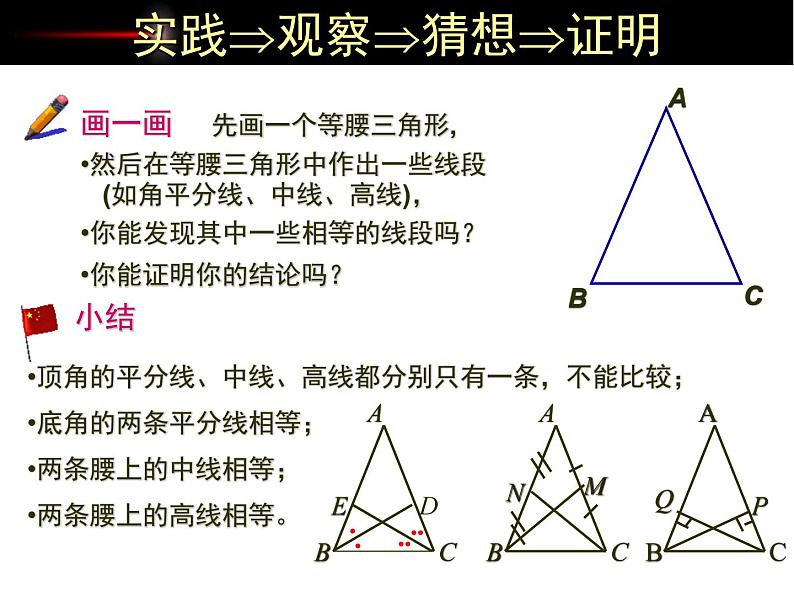
实践观察猜想证明
然后在等腰三角形中作出一些线段 (如角平分线、中线、高线)，
你能发现其中一些相等的线段吗？
顶角的平分线、中线、高线都分别只有一条，不能比较；底角的两条平分线相等；两条腰上的中线相等；两条腰上的高线相等。
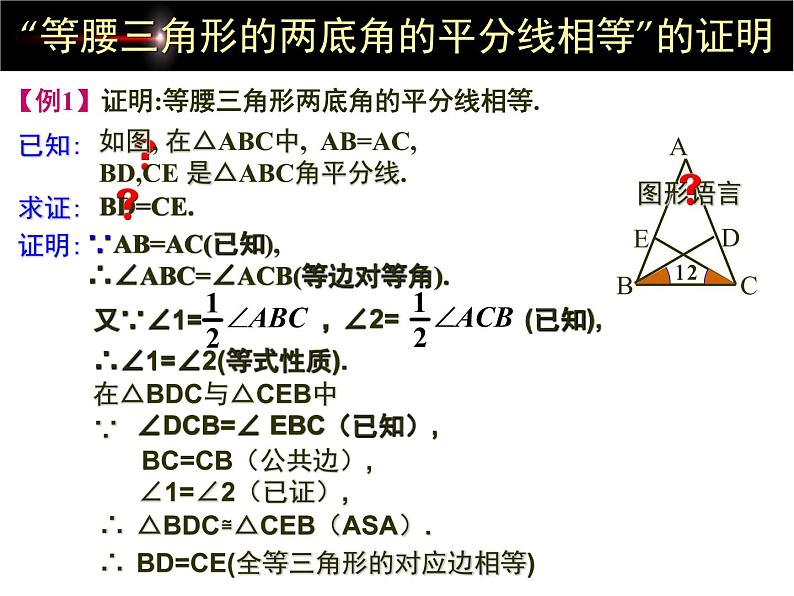
“等腰三角形的两底角的平分线相等”的证明
【例1】证明:等腰三角形两底角的平分线相等.
∵AB=AC(已知),∴∠ABC=∠ACB(等边对等角).
如图, 在△ABC中, AB=AC, BD,CE 是△ABC角平分线.
∴∠1=∠2(等式性质).
∠DCB=∠ EBC（已知）,
BC=CB（公共边）,
　∠1=∠2（已证）,
△BDC≌△CEB（ASA）.
BD=CE(全等三角形的对应边相等)
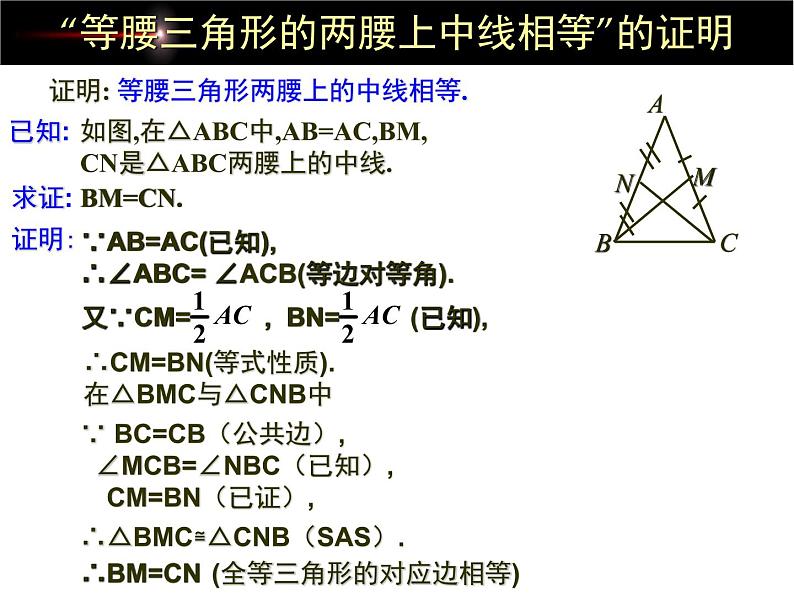
“等腰三角形的两腰上中线相等”的证明
证明: 等腰三角形两腰上的中线相等.
如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.
“等腰三角形两腰上的高相等”的证明
证明: 等腰三角形两腰上的高相等.
证明: ∵AB=AC(已知), ∴∠ABC=∠ACB(等边对等角). 又∵ BP,CQ是△ABC两腰上的高(已知), ∴∠BPC= ∠CQB=90(高的意义). 在△BPC与△CQB中 ∵∠BPC=∠CQB（已证）, 　 ∠PCB=∠QBC（已证）, BC=CB（公共边）, ∴△BPC≌△CQB（SAS）. ∴BP=CQ(全等三角形的对应边相等)
已知: 如图, 在△ABC中, AB=AC,BP,CQ是△ABC两腰上的高.求证: BP=CQ.
等腰三角形中的相等的线段(2)
这里是一个由特殊结论归纳出一般结论的一种数学思想方法.
(3)你能证明得到的结论吗？
由此你能得到一个什么结论?
过底边的端点且与底边夹角相等的两线段相等.
两腰上距顶点等距的两点与底边顶点的连线段相等.
等腰三角形的 判 定 定 理
你是如何思考的?请与同伴交流你的做法.
2. 前面已经证明了“等边对等角”，反过来，“等角对等边”吗?即有两个角相等的三角形是等腰三角形吗?
要证明AB=AC,只要能构造出AB，AC所在的两个三角形全等就可以了.
如：作BC边上的中线； 作∠A的平分线或作BC边上的高.
有两个角相等的三角形是等腰三角形（等角对等边）.
在△ABC中∵∠B＝∠C（已知），∴AB=AC（等角对等边）.
这又是一个判定两条线段相等的依据之一.
论证命题的新思维与新方法
小明说,在一个三角形中，如果两个角不相等,那么这两个角所对的边也不相等.
在△ABC中, 如果∠B≠∠C,那么AB≠AC.
你认为这个结论成立吗? 如果成立,你能证明它吗?
如图,在△ABC中,已知∠B≠∠C,此时,AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等角对等边”定理可得∠B=∠C, 但已知条件是 ∠B≠∠C.“∠B=∠C”与“∠B≠∠C”相矛盾，因此， AB≠AC.
你能理解他的证明过程吗?
论证的新方法----反证法
小明在证明时，先假设命题的结论不成立，然后推导出与定义，公理、已证定理或已知条件相矛盾的结果，从而证明便是的结论一定成立.这种证明方法称为反证法(reductin t absurdity)
你可要结识“反证法”这个新朋友噢!
假设AB=AC, 那么根据“等角对等边”定理可得∠B=∠C . 但已知条件是∠B≠∠C. “∠B=∠C”与“∠B≠∠C”相矛盾,因此,AB≠AC.
反证法是一种重要的数学证明方法.在解决某些问题时常常会有出人意料的作用.
用反证法证题的一般步骤
1. 假设: 先假设命题的结论不成立;2. 归谬: 从这个假设出发,应用正确的推论方法, 得出与定义，公理、已证定理或已知条件 相矛盾的结果;3. 结论: 由矛盾的结果判定假设不正确, 从而肯定命题的结论正确.
1.用反证法证明：一个三角形中不能有两个角是直角．已知：△ABC．求证：∠A、∠B、∠C中不能有两个角是直角．
分析：按反证法证明命题的步骤，首先要假定结论“∠A、∠B、∠C中不能有两个角是直角”不成立，即它的反面“∠A、∠B、∠C中有两个角是直角”成立，然后，从这个假定出发推下去，找出矛盾．
证明：假设∠A、∠B、∠C中有两个角是直角，不妨设∠A=∠B=90°，则∠A+∠B+∠C=90°+90°+∠C＞180°．这与三角形内角和定理矛盾，∠A=∠B=90°不成立．所以一个三角形中不能有两个角是直角．
2.用反证法证明：在一个三角形中, 至少有一个内角小于或等于600.