2020-2021学年1 等腰三角形授课课件ppt

这是一份2020-2021学年1 等腰三角形授课课件ppt，共11页。PPT课件主要包含了本节课学些什么等内容，欢迎下载使用。

2、了解作为证明基础的几条公理的内容， 掌握证明的基本步骤和书写格式。
3、经历“探索－发现－猜想－证明”的过程。能够用综合法证明等腰三角形的有关性质定理和判定定理。
能够用综合法证明等腰三角形的有关性质定理和判定定理。
了解作为证明基础的几条公理的内容，掌握证明的基本步骤和书写格式。
1、回顾与巩固上学期证明的有关内容;
几何的三种语言、平行线的判定
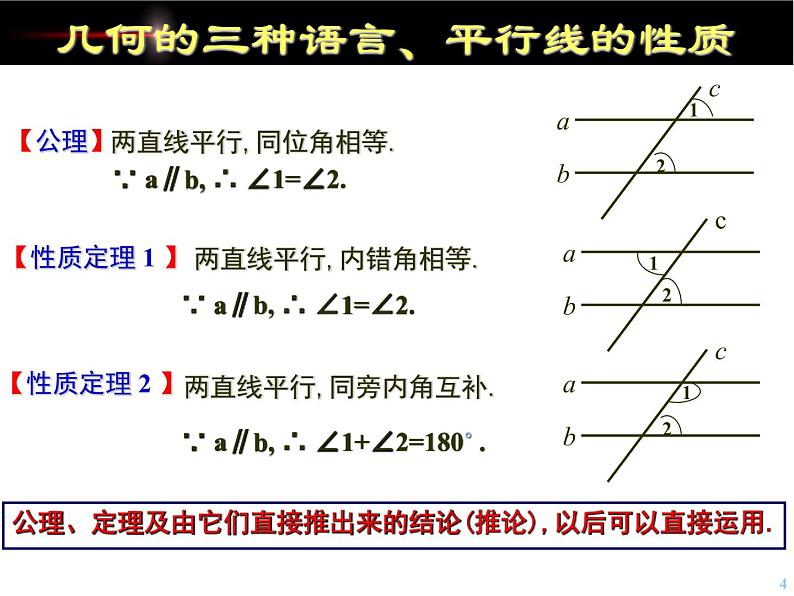
公理、定理及由它们直接推出来的结论(推论),以后可以直接运用.
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
∵∠1+∠2=180˚ , ∴ a∥b.
几何的三种语言、平行线的性质
两直线平行,同位角相等.
∵ a∥b, ∴ ∠1=∠2.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
∵ a∥b, ∴ ∠1+∠2=180˚ .
有关三角形全等的一些结论
三边对应相等的两个三角形全等 .
两边及其夹角对应相等的两个三角形全等 .
两角及其夹边对应相等的两个三角形全等 .
全等三角形的确对应边、对应角相等.
两角及其一角的对边对应相等的两个三角形全等 .
学好几何的标志是会“证明”
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言 写出“已知”和“求证”;
(4)分析题意,探索证明思路
(5)依据思路,运用数学符号和数学语言 条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
(由“因”导“果”,执“果”索“因”.);
等腰三角形的性质——的验证与证明
(2) 你能动手来证明这些结论吗吗？
等腰三角形的两个底角相等.
“等边对等角”——由实验到论证
(3) 你能利用已有的公理和定理 来证明“等边对等角”这一结论吗 ？
不难发现折痕两旁的的两个三角形全等。
由此实验得到启发——折痕就是我们用于证明时要添加的辅助线。
注意千万不要忘记书写的基本格式——
写“已知”、“求证”、“证明”。
等腰三角形的 “三线合一”
在上述问题中，折痕AD
是等腰三角形ABC的怎样的线？
线段AD的还具有怎样的性质？
由此你能得到什么结论？
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。
“等边对等角”定理 的推论：
线段AD是BC边的中线、
随堂练习 学好数学的诀窍
1、证明：等边三角形的三个角都相等，并且每个角都等于60˚。