北师大版九年级上册2 矩形的性质与判定评课课件ppt

这是一份北师大版九年级上册2 矩形的性质与判定评课课件ppt，共19页。PPT课件主要包含了请你思考，能证明它的正确性吗，活动一，活动二，二判断题，变式一，这节课你有什么收获，矩形的判定口诀等内容，欢迎下载使用。
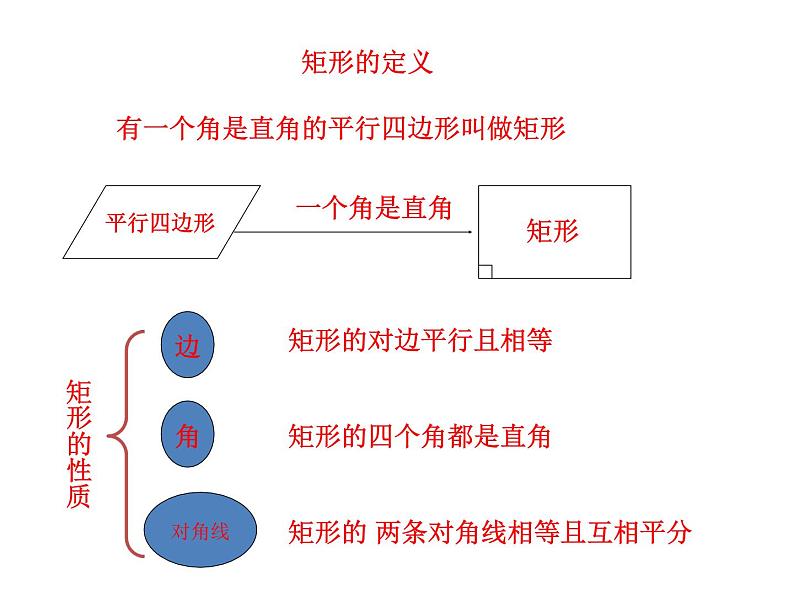
有一个角是直角的平行四边形叫做矩形
矩形的 两条对角线相等且互相平分
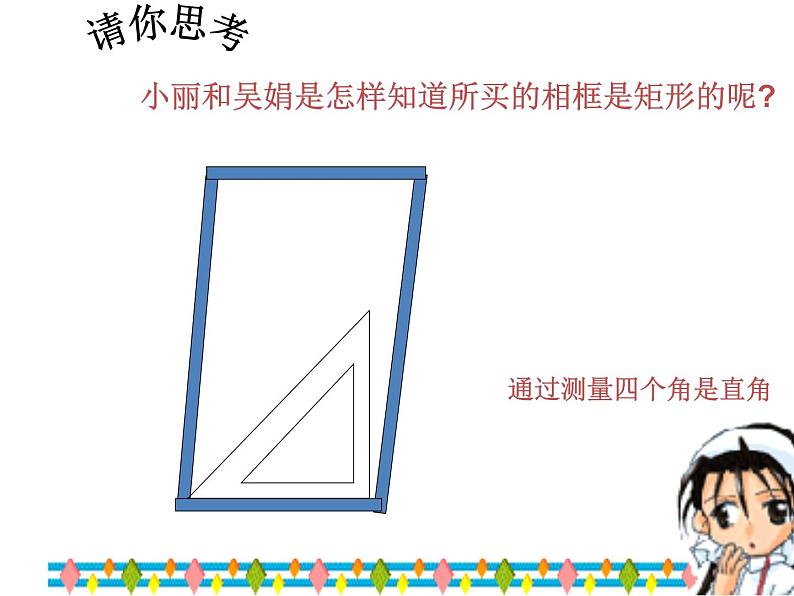
小丽和吴娟是怎样知道所买的相框是矩形的呢?
有三个角是直角的四边形是矩形吗?
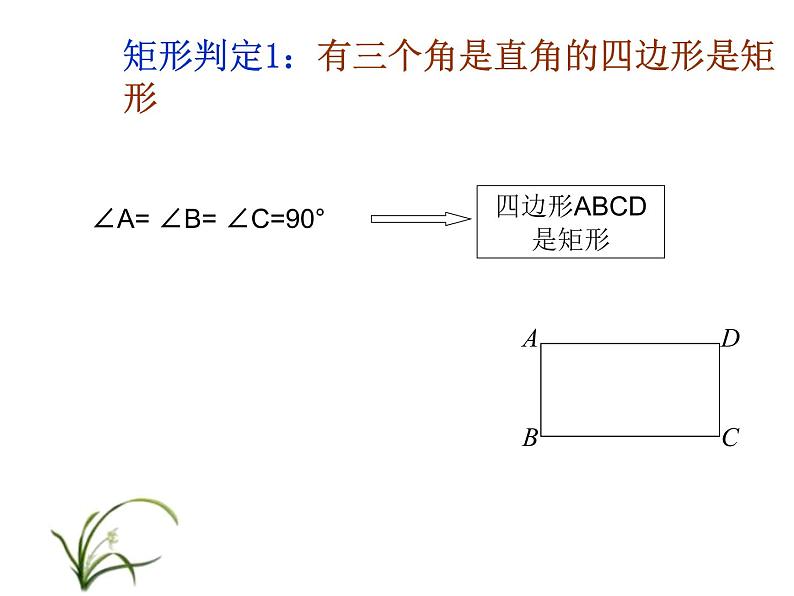
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
矩形判定1：有三个角是直角的四边形是矩形
除度量角度之外,她们需要度量什么也能知道做好的相框是矩形呢?
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD +∠CDA=180°
∴∠BAD＝90°
∴四边形ABCD是矩形（有一个内角是直角的平行四边形是矩形）
对角线相等的平行四边形是矩形吗？
四边形ABCD是平行四边形,AC=BD
矩形判定2：对角线相等的平行四边形是矩形
推论:对角线互相平分且相等的四边形是矩形
1、为了庆祝十一国庆节，八年级（3）班同学要在广场上布置一个矩形的花坛。计划用“串红”摆成两条对角线。如果一条对角线用了37盆“串红”，还 需要从花房运来多少盆“串红”？为什么？如果一条对角线用了48盆呢？为什么？
（1）矩形具有而平行四边形不具有的性质（ ）（A）内角和是360度（B）对角相等（C）对边平行且相等（D）对角线相等
（2）下面性质中，矩形不一定具有的是（ ）（A）对角线相等（B）四个角相等（C）是轴对称图形（D）对角线垂直
对角线相等的四边形是矩形。对角线互相平分且相等的四边形是矩形。有一个角是直角的四边形是矩形。四个角都是直角的四边形是矩形。四个角都相等的四边形是矩形。对角线相等且有一个角是直角的四边形是矩形。对角线相等且互相垂直的四边形是矩形。
例 1 已知：如图．矩形ABCD的对角线AC、BD相交于点O，且E、F、G、H分别是AO、BO、CO、DO的中点，求证四边形EFGH是矩形．
∵四边形ABCD是矩形
∴AC=BD（矩形的对角线相等)
AO=BO=CO=DO（矩形的对角线互相平分）
∵ E、F、G、H分别是AO、BO、 CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形（对角线互相平分的四边形是平行四边形）
∵EO+OG=FO+OH
∴四边形EFGH是矩形（对角线相等的平行四边形是矩形）。
已知：如图,矩形ABCD的对角线AC、BD相交于点O，E、F、G 、 H分别是AO 、BO 、 CO 、 DO上的一点 ,且AE=BF=CG=DH.
求证:四边形EFGH是矩形
任意一个四边形，三角直角定矩形。对于平行四边形，一个直角即可定；对线相等也矩形。