






初中数学北师大版七年级下册3 探索三角形全等的条件获奖课件ppt
展开北师大版七年级数学下册 4.3.2 用“角边角”“角角边” 判定三角形全等
学习目标
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.2.会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等.
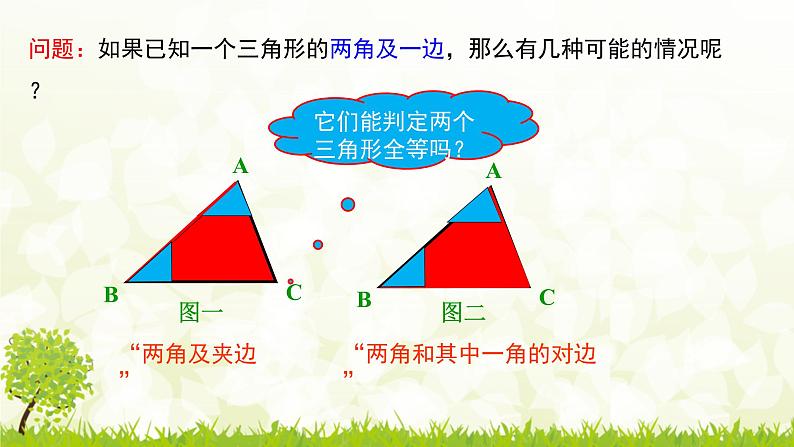
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
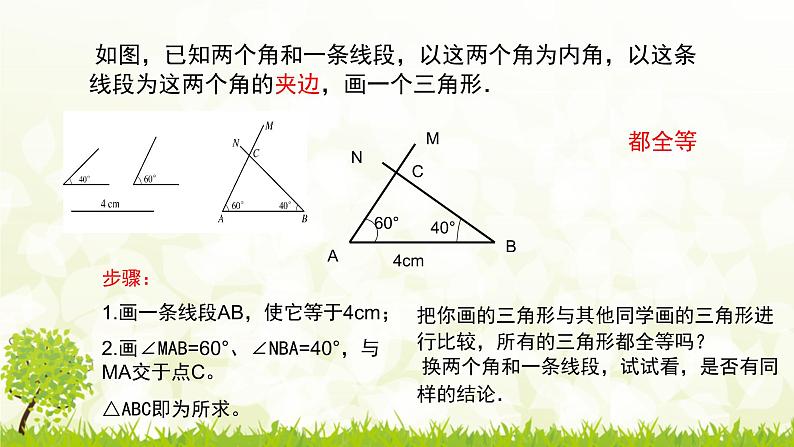
如图,已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.
步骤:1.画一条线段AB,使它等于4cm;2.画∠MAB=60°、∠NBA=40°,与MA交于点C。△ABC即为所求。
把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗? 换两个角和一条线段,试试看,是否有同样的结论.
60°
40°
4cm
A
B
C
M
N
都全等
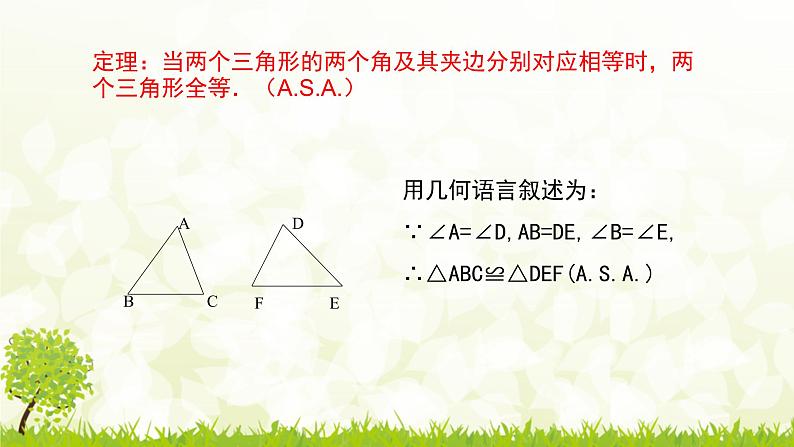
定理:当两个三角形的两个角及其夹边分别对应相等时,两个三角形全等.(A.S.A.)
用几何语言叙述为:∵∠A=∠D,AB=DE,∠B=∠E,∴△ABC≌△DEF(A.S.A.)
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
已知:∠A=∠A′,∠B=∠B′,AC=A′C′
求证:△ABC≌△A′B′C′
证明:∵ ∠A=∠A′,∠B=∠B′, ∠A+∠B+∠C=180° ∠A′+∠B′+∠C′=180° ∴ ∠C=∠C′. 在△ABC和△A′B′C′中, ∵ ∠A=∠A′ AC=A′C′ ∠C=∠C′ ∴ △ABC≌△A′B′C′(A.S.A.)
有两角和它们中一组等角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。
结论:
几何语言:在△ABE和△A′CD中,∵∠B=∠C(已知 ) ∠A=∠A′ (已知 ) AE=A′D(已知 ) ∴ △ABE≌△A′CD(AAS)
1.在利用“ASA”书写两个三角形全等的条件时,一般把夹边相等写在中间,以突出角的位置。
2."AAS"这一判定方法是由"ASA"结合三角形的内角和定理推出来的.
3."AAS"是指两角和其中一组等角的对边相等,千万不要认为是两角和一边相等"。
(1)AC∥BD,CE=DF,__ _.(SAS) (2) AC=BD, AC∥BD ,__________. (ASA)(3) CE=DF, , . (ASA)(4)∠ C= ∠D, , . (ASA)
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
AC=BD
∠A=∠B
例题1
例题2
已知:∠ABC=∠DCB,∠ACB= ∠DBC,试说明:△ABC≌△DCB.
∠ABC=∠DCB(已知), BC=CB(公共边), ∠ACB=∠DBC(已知),
解:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
判定方法:两角和它们的夹边对应相等两个三角形全等.
例题3
已知:如图,在△ABC中,D是边BC的中点,过点C画直线CE,使CE∥AB,交AD的延长线于点E.求证:AD=ED.
A
B
E
C
D
证明:
∴AD=ED(全等三角形的对应边相等).
∴ △ABD≌△ECD(AAS).
∵ CE∥AB(已知),
∴ ∠ABD=∠ECD,∠BAD=∠CED (两直线平行,内错角相等).
A
B
E
C
D
在△ABD和△ECD中,
∵ ∠ABD=∠ECD,∠BAD=∠CED
BD=CD(已知),
例题4
点B,E,C,F在同一条直线上,BC=EF,AB∥DE, ∠A=∠D.求证:△ABC≌△DEF.
例题5
已知:如图,△ABC ≌△A′B′C′ ,AD、A′ D′ 分别是△ABC 和△A′B′C′的高.试说明AD= A′D′ ,并用一句话说出你的发现.
解:因为△ABC ≌△A′B′C′ ,所以AB=A'B'(全等三角形对应边相等),∠ABD=∠A'B'D'(全等三角形对应角相等).因为AD⊥BC,A'D'⊥B'C',所以∠ADB=∠A'D'B'.在△ABD和△A'B'D'中,∠ADB=∠A'D'B'(已证),∠ABD=∠A'B'D'(已证),AB=AB(已证),所以△ABD≌△A'B'D'.所以AD=A'D'.
结论:全等三角形对应边上的高也相等.
1.要证明两条线段(或两个角)相等,可以通过这两条线段(或两个角)所在的两个三角形全等来证明.
2.两角分别相等且其中一组对角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
注意“角角边”、“角边角”中两角与边的区别
3.有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)
谢谢观看
北师大版七年级下册3 探索三角形全等的条件精品备课课件ppt: 这是一份北师大版七年级下册<a href="/sx/tb_c9990_t3/?tag_id=26" target="_blank">3 探索三角形全等的条件精品备课课件ppt</a>,文件包含432《利用“角边角”判定三角形全等》课件pptx、432《利用“角边角”判定三角形全等》教案doc、432《利用“角边角”判定三角形全等》练习doc、432《利用“角边角”判定三角形全等》学案doc等4份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学北师大版七年级下册3 探索三角形全等的条件多媒体教学ppt课件: 这是一份初中数学北师大版七年级下册3 探索三角形全等的条件多媒体教学ppt课件,共23页。PPT课件主要包含了情境引入,学习目标,导入新课,“两角及夹边”,讲授新课,作图探究,“角边角”判定方法,几何语言,∴ADAE,合作探究等内容,欢迎下载使用。
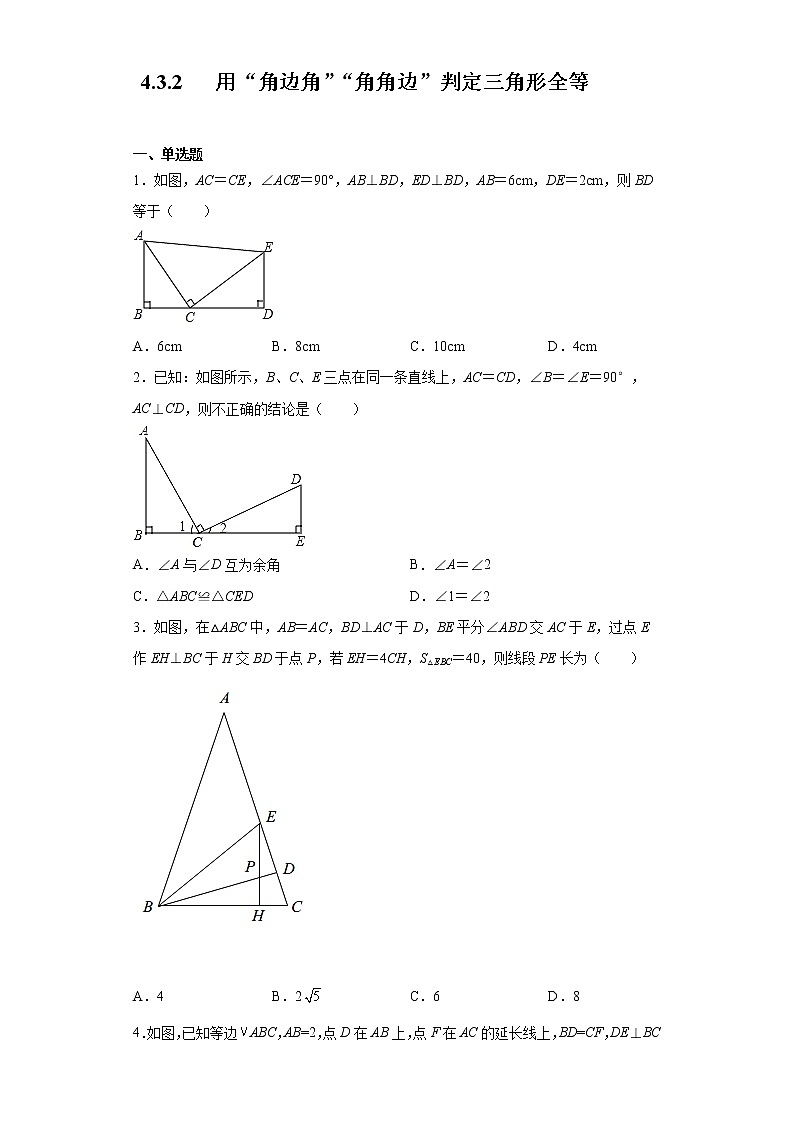
初中数学3 探索三角形全等的条件习题课件ppt: 这是一份初中数学3 探索三角形全等的条件习题课件ppt,文件包含43第2课时角边角与角角边ppt、43-2ppt、43第2课时利用“角边角”“角角边”判定三角形全等docx、asa432wmv等4份课件配套教学资源,其中PPT共38页, 欢迎下载使用。














