北京市西城区三帆中学2021~2022学年九年级上学期期中考试数学【试卷+答案】

这是一份北京市西城区三帆中学2021~2022学年九年级上学期期中考试数学【试卷+答案】，共13页。
班级＿＿＿＿＿ 姓名＿＿＿＿＿ 学号＿＿＿ 成绩＿＿＿＿＿
注意：（1）时间120分钟，满分100分；（2）请将答案填写在答题纸上。
一、选择题(本题共16分，每小题2分)
1． 下列四个图形中，不是中心对称图形的是（ ）．

A． B． C． D．
2． 如图，点A，B，C均在⊙O上，∠BOC＝100°，则∠BAC的度数
为（ ）．
A．70° B．60° C．50° D．40°
3． 若方程是关于x的一元二次方程，则m的值为（ ）．
A．1 B． C．±1 D．不存在
4． 方程的根的情况是（ ）．
A．有两个不相等实数根 B．有两个相等实数根
C．没有实数根 D．无法判断
5． 将抛物线向左平移1个单位，再向上平移3个单位得到的表达式是（ ）．
A． B．
C． D．
6． 如图，AB是⊙O的直径，点C是⊙O上一点，若∠BAC=30°，BC=2，则AB的长为（ ）．
A．2 B．4 C．6 D．8
7． 如图，PA，PB分别与⊙O相切于A，B两点，PA=AB，
则∠AOB=（ ）．
A． 100°B． 110°C． 120°D． 130°
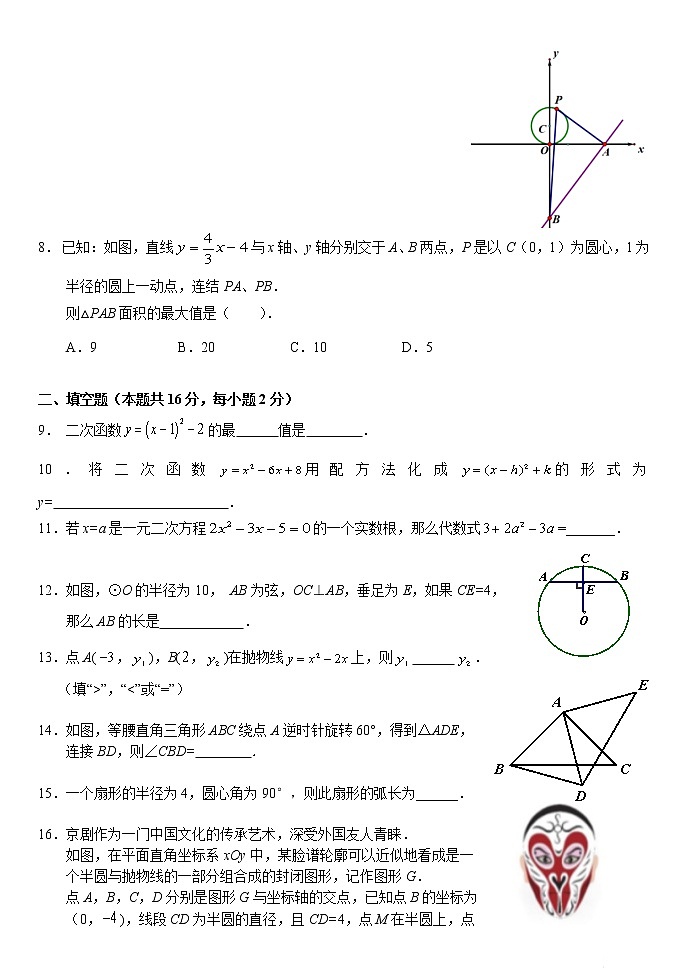
8． 已知：如图，直线与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB．
则△PAB面积的最大值是（ ）．
A．9 B．20 C．10 D．5
二、填空题（本题共16分，每小题2分）
9．二次函数的最 值是 ．
10．将二次函数用配方法化成的形式为y= ．
11．若x=a是一元二次方程的一个实数根，那么代数式=_______．
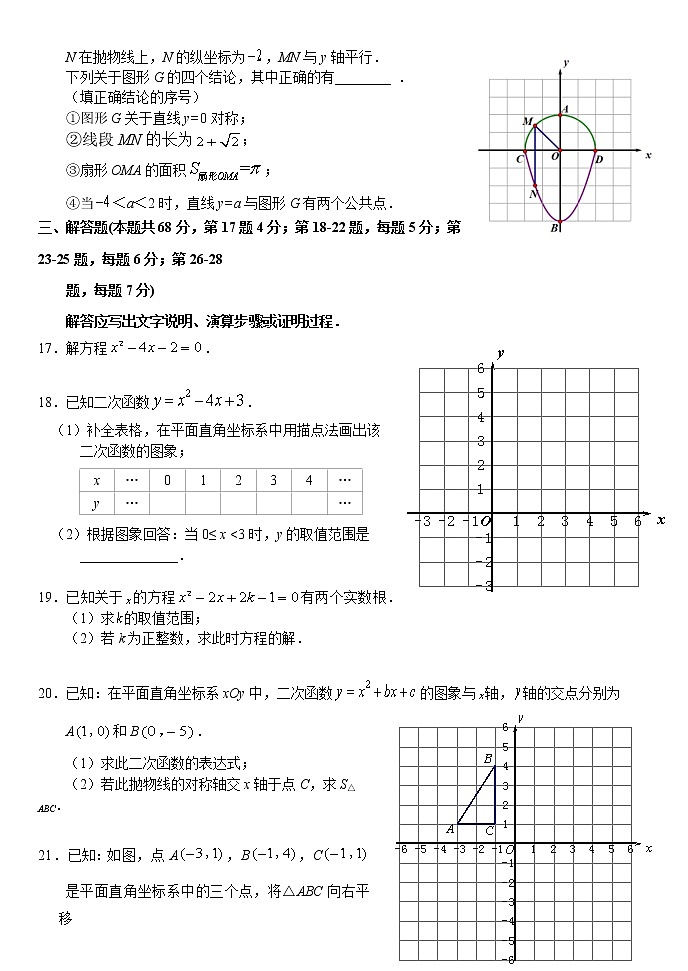
12．如图，⊙O的半径为10， AB为弦，OC⊥AB，垂足为E，如果CE=4，
那么AB的长是 ．
13．点A(，)，B(，)在抛物线上，则 ．
（填“>”，“；14. 15°；15. 2π；16. ②④.
三、解答题
17. 解：公式法：
或配方法：
18. （1）
…………………………1分
画图…………………………3分
（2）…………………………5分
19. （1）∵方程有两个不相等的实数根
∴△ ≥0…………………………1分
∵△=22-42k-1=8-8k≥0 …………………………2分
∴k≤1…………………………3分
∵k为正整数,k≤1
∴k=1 …………………………4分
∴x2-2x+1=0
∴解得∴x1=x2=1…………………………5分
20. 解：（1）交点代入得：
∴． …………… 2分
解得： ． …………… 3分
∴抛物线的表达式为：．
（2） 抛物线对称轴是直线，∴C点（－2，0）…………… 4分
…………… 5分
21. （1）画图…………………………2分
（2）画图…………………………4分
点B2的坐标为（-2，-4）…………………………5分
22. （1）解：
（2）元………………………5分
23. 连接AE得1分，两弧交出点B得1分，连接OB交圆O于点C得1分，做直线AC得1分，共4分；
等腰三角形底边中线与底边高线重合（或者写等腰三角形三线合一）-----5分
过半径外端并且垂直于这条半径的直线是圆的切线------6分.
24. （1）x1＋x2＝ ，x1·x2＝2；………………2分
（2）C………………4分
（3）x1·x2=-5. ………………6分
25.
(2) 补全图形-------------4分
求出------5分；------6分；
26. 解：（1）∵抛物线经过点（3，0），
∴9m－6m+m+4=0，………………………………………………1分
∴m=－1.
∴y=－x2+2x+3. ………………………………………………………2分
（2） ∵y=－x2+2x+3=－(x－1)2+4，∴该抛物线的顶点为（1，4）. …………3分
∴当直线经过顶点（1，4）时t与图象G有公共点，此时t =4.
∵该抛物线与y轴的交点为（0，3）.∴此时t =3. ………………………4分
∴ 3＜t≤4. ………………………5分
（3）－2＜m≤－1. ………………………7分
27. （1）40 ---------------- 2分
（2）①设∠FAD=α，∠DAC=β，
∵AE=EF
∴∠AFE=∠FAC=∠FAD+∠DAC=α+β．
∴∠FEC=∠AFE+∠FAC=2α+2β．
∵AD为∠BAC的平分线，
∴∠BAC=2∠DAC=2∠BAD =2β．
∴∠AGE=∠FEC∠BAC=2α． ---------------- 3分
∵OG=OA
∴∠AGE=∠BAD=∠GAF+∠FAD=2α．
∴∠GAF=∠DAF=α， ---------------- 4分
∴△AGF≅△ADF ---------------- 5分
∴GF=FD
（3）∠FAC=∠DAC±30 ---------------- 7分
28. （1）当OH=OI=2时，R∠MON的最小值是_____1____________；. ………………1分
当OH=2，弧HI是半圆时，求线段OI长度的取值范围；
评标：当时
∵OH=2，∠MON=60°
∴=1………………2分
当OM⊥HI2时
∵OH=2，∠MON=60°
∴=4………………3分
综上………………4分
（3）当OH≤OI，R∠MON=3，l弧HI=2π时，求线段OI长度的范围；
评标：∵R∠MON=3，l弧HI=2π
∴∠HAI=120°………………5分
∴OI=6. ………………6分
∵∠MON=60°，∠HAI=120°
∴OI=OH=33.
∴………………7分
x
…
0
1
2
3
4
…
y
…
…
1
2
3
4
5
6
7
8
A
C
B
A
D
B
C
C
x
…
0
1
2
3
4
…
y
…
3
0
-1
0
3
…