

所属成套资源:2022高考数学圆锥曲线40个专题(含解析)
- 专题14:双曲线的定义与方程23页 试卷 7 次下载
- 专题15:双曲线的对称性问题16页 试卷 7 次下载
- 专题17:双曲线的定点问题19页 试卷 7 次下载
- 专题18:双曲线的定值问题25页 试卷 7 次下载
- 专题19:双曲线的定直线问题9页 试卷 7 次下载
专题16:双曲线的离心率问题34页
展开这是一份专题16:双曲线的离心率问题34页,共35页。试卷主要包含了单选题,填空题等内容,欢迎下载使用。
专题16:双曲线的离心率问题
一、单选题
1.已知点是抛物线的对称轴与准线的交点,点为抛物线的焦点,点在抛物线上且满足,若取最大值时,点恰好在以为焦点的双曲线上,则双曲线的离心率为
A. B. C. D.
2.是双曲线的左、右焦点,直线l为双曲线C的一条渐近线,关于直线l的对称点为,且点在以F2为圆心、以半虚轴长b为半径的圆上,则双曲线C的离心率为
A. B. C.2 D.
3.已知双曲线的左、右顶点分别为、,是上一点,为等腰三角形,且外接圆面积为,则双曲线的离心率为
A. B. C. D.
4.设点,分别为双曲线的左右焦点.点,分别在双曲线的左,右支上,若,且,则双曲线的离心率为( )
A. B. C. D.
5.已知双曲线的右顶点、右焦点分别为A,,过点A的直线与的一条渐近线交于点,直线与的一个交点为B,若,且,则的离心率为( )
A.2 B. C. D.
6.已知,是双曲线:的左,右焦点,过点倾斜角为30°的直线与双曲线的左,右两支分别交于点,.若,则双曲线的离心率为( )
A. B. C.2 D.
7.已知双曲线的右焦点为F,关于原点对称的两点A、B分别在双曲线的左、右两支上,,且点C在双曲线上,则双曲线的离心率为( )
A. B. C. D.2
8.已知是双曲线的左右两个焦点,若双曲线左支上存在一点P与点关于直线对称,则该双曲线C的离心率为( )
A. B. C. D.
9.已知,分别为双曲线的左,右焦点,过点的直线与双曲线的右支交于,两点,设点,分别为,的内心,若,则双曲线离心率的取值范围为( )
A. B. C. D.
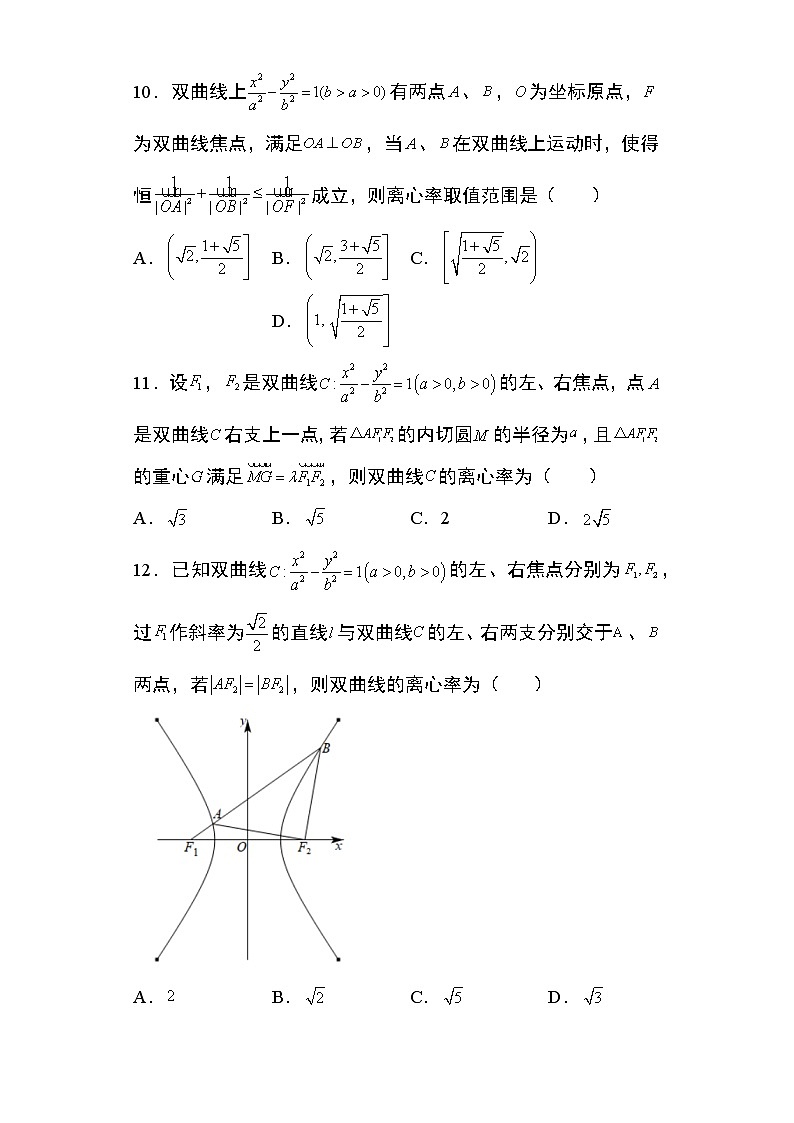
10.双曲线上有两点、,为坐标原点,为双曲线焦点,满足,当、在双曲线上运动时,使得恒成立,则离心率取值范围是( )
A. B. C. D.
11.设,是双曲线的左、右焦点,点是双曲线右支上一点,若的内切圆的半径为,且的重心满足,则双曲线的离心率为( )
A. B. C.2 D.
12.已知双曲线的左、右焦点分别为,过作斜率为的直线与双曲线的左、右两支分别交于、两点,若,则双曲线的离心率为( )
A. B. C. D.
13.已知,分别为双曲线的左,右焦点,点A为双曲线C的右顶点,且直线与双曲线C的左、右两支分别交于P,Q两点,若,则双曲线C的离心率的取值范围为( )
A. B. C. D.
14.已知双曲线的左、右焦点分别为、,分别是双曲线左、右两支上关于坐标原点对称的两点,且直线的斜率为,分别为、的中点,若原点在以线段为直径的圆上,则双曲线的离心率为( )
A. B. C. D.
15.若双曲线:绕其对称中心旋转后可得某一函数的图象,则的离心率等于( )
A. B. C.2或 D.2或
16.已知为双曲线的右焦点,、是双曲线的一条渐近线上关于原点对称的两点,,且的中点在双曲线上,则的离心率为
A. B. C. D.
17.双曲线的左右焦点为,一条渐近线方程为,过点且与垂直的直线分别交双曲线的左支及右支于,满足,则该双曲线的离心率为( )
A. B.3 C. D.2
18.已知双曲线的左、右焦点分别为,过的直线与的左支交于,两点,若,且,则的离心率为( )
A. B. C. D.
19.设双曲线的左、右顶点分别为,,点C在双曲线上,的三个内角分别用,,表示,若,则双曲线的离心率为( )
A. B. C.2 D.
20.设双曲线的上焦点为F,过点F作与y轴垂直的直线交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若,,则双曲线的离心率e的值是( )
A.3 B. C. D.
21.已知是方程的一个根,另两个实根可分别作为某椭圆,某双曲线的离心率,则的取值范围是( )
A. B. C. D.
二、填空题
22.已知双曲线的左右顶点分别是,右焦点,过垂直于轴的直线交双曲线于两点,为直线上的点,当的外接圆面积达到最小时,点恰好落在(或)处,则双曲线的离心率是__________.
23.已知是椭圆与双曲线的公共焦点,是它们的一个公共点,且,线段的垂直平分线过,若椭圆的离心率为,双曲线的离心率为,则的最小值为____________.
24.已知双曲线的焦点为,是双曲线上一点,且.若的外接圆和内切圆的半径分别为,且,则双曲线的离心率为__________.
25.如图,已知双曲线的左、右焦点分别为,,M是C上位于第一象限内的一点,且直线与y轴的正半轴交于A点,的内切圆在边上的切点为N,若,则双曲线C的离心率为________.
26.双曲线上一点P,过双曲线中心O的直线交双曲线于A、B两不同(点A,B异于点P).设直线PA、PB的斜率分别为、,当最小时,双曲线的离心率为_______.
27.已知双曲线的右焦点为,过且斜率为的直线交于、两点,若,则的离心率为______.
参考答案
1.B
【解析】过P作准线的垂线,垂足为N,则由抛物线的定义可得|PN|=|PB|,
∵|PA|=m|PB|, ∴|PA|=m|PN| ∴,
设PA的倾斜角为,则,
当m取得最大值时,最小,此时直线PA与抛物线相切,
设直线PA的方程为y=kx﹣1,代入x2=4y,可得x2=4(kx﹣1),即x2﹣4kx+4=0,
∴△=16k2﹣16=0,∴k=±1, ∴P(2,1),
∴双曲线的实轴长为PA﹣PB=2(﹣1), ∴双曲线的离心率为.
故选B.
【点评】本题的关键是探究m的最大值,先利用抛物线的定义转化得到,m取得最大值时,最小,此时直线PA与抛物线相切,得到△=0,得到k的值.转化是高中数学很重要的一个数学思想,在解题过程中要注意灵活运用.
2.B
【分析】根据左焦点与渐近线方程,求得关于直线l的对称点为,写出以F2为圆心、以半虚轴长b为半径的圆的方程,再将代入圆的方程,化简即可得离心率.
【解析】因为直线l为双曲线C的一条渐近线,则直线
因为是双曲线的左、右焦点
所以(-c,0),(c,0)
因为关于直线l的对称点为,设为(x,y)
则
解得
所以为()
因为是以为圆心,以半虚轴长b为半径的圆,则圆的方程为
将以的()代入圆的方程得
化简整理得 ,所以
所以选B
【点评】本题考查了双曲线渐近线方程、离心率的应用,点关于直线对称点的求法,对于几何关系的理解非常关键,属于难题.
3.C
【分析】不妨设在第二象限,由外接圆面积得其半径,设,利用正弦定理求出,从而可得,然后求得点坐标,把点坐标代入双曲线方程可得关系式,化简后可求得离心率.
【解析】不妨设在第二象限,则在等腰中,,
设,则,为锐角.
外接圆面积为,则其半径为,∴,
∴,,
∴,,
设点坐标为,则,,
即点坐标为,
由点在双曲线上,得,整理得,
∴.
故选C.
【点评】本题将解三角形和双曲线的几何性质结合在一起考查,综合性较强,解题时要抓住问题的关键和要点,从所要求的离心率出发,寻找双曲线中之间的数量关系,其中通过解三角形得出点的坐标,是解题的突破点,在得到点坐标后,根据点在双曲线上得出间的关系,最后根据可求得离心率.
4.B
【分析】由及数量积的运算律可得,设,则,,利用双曲线的定义及直角三角形可求得(不合题意舍去),然后求出,再用余弦定理得出关系求得离心率.
【解析】,共线,且,
,
,则,故有,
设,则,,QQ群333528558由双曲线的定义可得
∴,整理得,解得:或,
若,则,,不满足,舍去;
若,,符合题意,则,,
此时,
在中,,
即,得到,即,
∴.
故选:B.
【点评】关键点【点评】本题主要考查双曲线的定义、双曲线的离心率及直线与双曲线的位置关系的应用,其中涉及到平面向量的线性运算和余弦定理,求解出是本题的解题关键,属于中档题.
5.C
【分析】由向量数量积等式推出l⊥x轴,求出点Q坐标,进而得点B坐标,再代入双曲线方程求解即得.
【解析】由已知得,设,
由,得,
所以轴,即,
不妨设点在第一象限,则.
设,由,得,
,
,即,
点在双曲线上,
,
整理得,,
解得,或(负值舍去).故选C.
故选:C
【点评】求解双曲线离心率的问题,根据条件建立关于a,b,c的齐次式,结合b2=c2-a2转化为a,c的齐次式,再转化为关于e的方程,解之即可得e.
6.A
【分析】设,据双曲线的定义可用表示,作,构造直角三角形可计算得,并用勾股定理列出了,进而可求.
【解析】设,则,
从而,进而.
过作,则.如图:
在中,,;
在中,,
即,所以.
故选:A
【点评】(1)焦点三角形为条件求圆锥曲线的离心率,常利用圆锥曲线的定义;
(2)求圆锥曲线的离心率,常利用有关三角形建立关于的齐次等式,再化为的等式可求;
(3)此题的关键是作得直角三角形,即可求出边长,又可用来建立的齐次等式.
7.B
【分析】由点A、B关于原点对称,设,则,利用,得,再利用得到关系式,再用点C、B在双曲线上,三个式子联立求解得到,化简得到,即可求得双曲线的离心率.
【解析】由点A、B关于原点对称,设,则
,设,,
,,即
,
利用向量数量积公式得:,即①
又点C、B均在双曲线上,
②,③
由①②③可得:
两边同时除以可得:
两边同时平方得;,即
又双曲线的离心率,则,即
故选:B.
【点评】关键点【点评】本题考查双曲线的离心率,解题关键是找到关于的等量关系.本题中利用得到点C坐标,利用点C、B均在双曲线上,得到关系式,再利用得到关系式,三个式子联立得到所要求的等量关系,考查了学生的运算求解能力,逻辑推理能力.属于中档题.
8.B
【分析】求出过焦点且垂直渐近线的直线方程,联立渐近线方程,解方程组可得对称中心的点的坐标,代入方程结合,解出即得.
【解析】由题意,设点焦点且垂直渐近线的直线方程为:,
由,解得:,,
所以,对称中心的点坐标为,又,设点,
则,解得,即点,
将点代入双曲线的方程可得,又,
化简可得,故.
故选:B.
【点评】本题考查双曲线的简单性质,考查双曲线离心率的求解和对称问题,属于中档题.
9.D
【分析】结合图形,由双曲线的定义及内切圆的性质可得,即,同理可得,从而可得,再由,可得,设直线的倾斜角为,在和中,分别将,用表示代入即可求出直线的斜率,再结合直线与双曲线右支交于两点,即可求出,进而可求出离心率的取值范围.
【解析】不妨设直线的斜率大于0.如图:
连接.,,设的内切圆与三边分别切于点,,,则
,
所以,即,同理可得,所以,
设直线的倾斜角为,在中,,
在中,,
又,所以,
即,解得,
所以,即直线的斜率为,
由题意,直线与双曲线右支交于两点,故,
所以.
故选:D
【点评】本题主要考查了结合平面几何知识求双曲线的离心率的取值范围,属于难题.
10.A
【分析】先根据得到,再联立直线方程和双曲线方程利用韦达定理化简得到,从而得到为定值,即可求解离心率.
【解析】设,直线:
因为,即
联立,整理得
,
代入得
所以
整理得
即由到直线:的距离
所以距离为一个定值
又
又
即
所以
又
所以
又
所以
故选:A
【点评】此题考查双曲线的离心率,难点是联立方程后的化简过程,对计算的要求较高,属于较难题目.
11.C
【分析】根据,得到,,然后由等面积法由,结合,解得,再利用距离公式得到,进而得到A的坐标,代入双曲线方程求解即可.
【解析】如图所示:
因为,
所以,
所以,,
所以,
又,
解得,
设,,
所以,
.
所以,
解得,
所以,代入双曲线方程得:,
解得,
所以.
故选:C
【点评】本题主要考查双曲线的第一定义和焦半径公式以及内切圆的应用,离心率的求法,还考查了数形结合的思想和运算求解的能力,属于难题.
12.D
【分析】取中点,连结,因为,所以可得,设,根据双曲线的定义求出,再由勾股定理得出,得出,再由直线的斜率为,即可求出离心率.
【解析】如图,因为,则取中点,连结,可得,设,因为,则,又因为,则,,则,则,
在中有,在中有,
所以,解得,因为直线的斜率为,
所以,所以,,
所以离心率.
故选:D
【点评】本题主要考查双曲线的性质即离心率的求法,解题的关键是找出双曲线中间的关系.
13.A
【分析】首先联立直线l与双曲线的方程,求得点P,Q的坐标,然后根据条件可推出,由此得到关于a,b的不等式,从而求得的范围,进而求得双曲线离心率的取值范围.
【解析】由,得,所以,.因为,所以,.又,所以,则,即,整理,得.因为,所以,所以,所以双曲线C的离心率,又,所以,
故选:A.
【点评】本题考查双曲线的几何性质、向量的数量积等,考查逻辑推理能力、运算求解能力、数形结合思想,考查的核心素养是逻辑推理,数学运算,属于较难题.
关于求解椭圆,双曲线的离心率问题,基本的解题思路是建立椭圆或双曲线中关于a,b,c的关系式,求值问题建立关于a,b,c的等式,求取值范围问题建立关于a,b,c的不等式.
14.A
【分析】设,点与点关于原点对称,分别为、的中点,可得出的坐标,再根据原点在以线段为直径的圆上,所以有,可得出与的关系,代入双曲线方程化简即可得出离心率.
【解析】设,则,,如图
分别为、的中点,
,,
原点在以线段为直径的圆上,
即,
解得:
故,
把代入双曲线方程可得:,
化简得:即,
解得:即
故选:A
【点评】本题考查了双曲线的几何性质及其应用,由题意得到和的关系,接下来解关于离心率的方程,考查了学生的计算能力,属于较难题.
15.C
【分析】由双曲线的几何性质与函数的概念可知,此双曲线的两条渐近线的夹角为,所以或,由离心率公式即可算出结果.
【解析】由双曲线的几何性质与函数的概念可知,此双曲线的两条渐近线的夹角为,又双曲线的焦点既可在轴,又可在轴上,所以或,或.
故选:C
【点评】本题主要考查了双曲线的简单几何性质,函数的概念,考查了分类讨论的数学思想.
16.A
【分析】由题知是直角三角形,是斜边中点,得 ,从而求出点坐标,得到点坐标,再代入双曲线方程化简可得离心率.
【解析】,是直角三角形,
点在渐近线上,设 ,
解得:
,
中点在双曲线上,代入方程:
化简得,则
故选:A.
【点评】本题考查求双曲线离心率.
求双曲线离心率的三种方法:
(1)直接求出来求解通过已知条件列方程组,解出的值.
(2)构造的齐次式,解出由已知条件得出关于的二元齐次方程,然后转化为关于离心率的一元二次方程求解.
(3)通过取特殊值或特殊位置,求出离心率.
在解关于离心率的二次方程时,要注意利用双曲线的离心率)进行根的取舍,否则将产生增根.
17.A
【分析】设,直线的方程为,联立方程得到,,根据向量关系化简到,得到离心率.
【解析】设,直线的方程为.
联立整理得,
则.
因为,所以为线段的中点,所以,,整理得,
故该双曲线的离心率.
故选:.
【点评】本题考查了双曲线的离心率,意在考查学生的计算能力和转化能力.
18.B
【分析】计算得到,, ,,根据,利用余弦定理得到,计算得到答案.
【解析】,故,
,故,故.
根据余弦定理,
,,
化简整理得到:,即,解得或(舍去).
故选:.
【点评】本题考查了双曲线离心率,意在考查学生的计算能力和综合应用能力.
19.A
【分析】由式子和可得:,进而可得出,设点在第一象限,分别求得,,代入可得:,最后求出离心率即可.
【解析】,,
∵,,
∴,即,
设点在第一象限,
则,,,,
∴,,
∴,.
故选:A.
【点评】本题考查两角和的正切公式,考查双曲线的简单几何性质,考查逻辑思维能力和计算能力,属于常考题.
20.C
【分析】根据三点共线得到,计算得到,代入双曲线方程,化简得到答案.
【解析】渐近线为:,取,解得,则.
,且三点共线,故,,
则 或,不妨取,则,
代入双曲线方程得到:,即.
故选:.
【点评】本题考查了双曲线的离心率,根据共线得到是解题的关键.
21.D
【分析】由题意,求出,分解函数的表达方式为一个一次因式与一个二次因式的乘积,通过函数的零点即可推出,的关系利用线性规划求解的取值范围即可.
【解析】依题意得,故,
所以.另外两根分别是一椭圆、一双曲线的离心率,故有两个分别属于和的零点.
故有且,即且.
运用线性规划知识,以横轴为,以纵轴为,
作出不等式组所表达平面区域,为阴影部分
可求得.
故选D.
【点评】椭圆离心率,双曲线离心率,本题考查函数零点问题,线性规划问题,综合性比较强,有一定难度.
22.
【解析】
【分析】设点的坐标为,求出点的坐标,由的外接圆面积取最小值时,取到最大值,则,利用基本不等式求出
的最小值,利用等号成立求出的表达式,令求出双曲线的离心率的值.
【解析】如下图所示,将代入双曲线的方程得,得,所以点,
设点的坐标为,由的外接圆面积取最小值时,则取到最大值,
则取到最大值,,,
,
当且仅当,即当时,等号成立,
所以,当时,最大,此时的外接圆面积取最小值,
由题意可得,则,此时,双曲线的离心率为,
故答案为.
【点评】本题考查双曲线离心率的求解,考查利用基本不等式求最值,本题中将三角形的外接圆面积最小转化为对应的角取最大值,转化为三角函数值的最值求解,考查化归与转化思想的应用,运算量较大,属于难题.
23.6
【分析】由于线段的垂直平分线过,所以有,再根据双曲线和椭圆的定义,求出的表达式,然后利用基本不等式来求得最小值.
【解析】设椭圆对应的参数为,双曲线对应的参数为,由于线段的垂直平分线过,所以有.根据双曲线和椭圆的定义有,两式相减得到,即.所以,即最小值为.
【点评】本小题考查双曲线的定义和几何性质,考查椭圆的定义和几何性质,是一个综合性较强的题目.由于椭圆和双曲线有公共的焦点,所以焦距相同,也就是有相同.对于两个曲线的公共交点来说,即满足椭圆的定义,又满足双曲线的定义,根据定义可列出方程.再利用基本不等式可求得最小值.
24..
【分析】在中,利用正弦定理:,求得,,设,再利用余弦定理求得,然后由求解.
【解析】双曲线的焦点为,
在中,由正弦定理得:,
解得,,
设,
在中,由余弦定理得:,
解得,
所以,
因为
又,
所以,则
所以
整理得,则
解得或(舍去)
故答案为:.
【点评】关键点【点评】本题的关键在于结合正余定理以及化简求解.
25.
【分析】根据双曲线的定义以及圆的切线定理得到,进而得到,求出,即可求出双曲线的离心率.
【解析】解:如图所示:设的内切圆在上的切点分别为,
由双曲线的定义知:,
即,
又,
即,
即,
又,
,
即,
则,
,
,
即,
,
故答案为:.
【点评】关键点【点评】本题解题的关键是利用双曲线的定义以及切线长定理得到.
26.2
【分析】设,,,显然,,又由点A,P在双曲线上得
,结合斜率公式可推得,令,构造函数,利用导数求出函数的最小值,然后计算出双曲线的离心率.
【解析】设,,,显然,.
∵点A,P在双曲线上,∴,
两式相减得,
∴,
∵,
设,则,
∴求导得,
∴在单调递减,在单调递增,
∴当时,取最小值,
此时.
故答案为:2
【点评】本题主要考查了双曲线的离心率的求解,利用导数求函数的最值,直线的斜率公式,考查了学生的运算求解能力.
27.
【分析】设,将直线的方程和双曲线的方程联立消元得出,由可得,这几个式子再结合化简可得
【解析】因为直线过点,且斜率为
所以直线的方程为:
与双曲线联立消去,得
设
所以
因为,可得
代入上式得
消去并化简整理得:
将代入化简得:
解之得
因此,该双曲线的离心率
故答案为:
【点评】1.直线与双曲线相交的问题,常将两个的方程联立消元,用韦达定理表示出横(纵)坐标之和、积,然后再结合条件求解
2.求离心率即是求与的关系.
相关试卷
这是一份专题12 双曲线中的离心率问题-备战2024年新高考数学之圆锥曲线专项高分突破(新高考专用),文件包含专题12双曲线中的离心率问题原卷版docx、专题12双曲线中的离心率问题解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
这是一份2024年高三培优讲义12---椭圆与双曲线离心率相关问题,共47页。
这是一份2023届新高考数学解析几何专题讲义 第18讲 双曲线的离心率问题












