湖北省新高考联考协作体2021-2022学年高二上学期期中考试数学试题

这是一份湖北省新高考联考协作体2021-2022学年高二上学期期中考试数学试题，文件包含高二数学答案doc、湖北省新高考联考协作体2021-2022学年高二上学期期中考试数学试题pdf等2份试卷配套教学资源，其中试卷共7页， 欢迎下载使用。
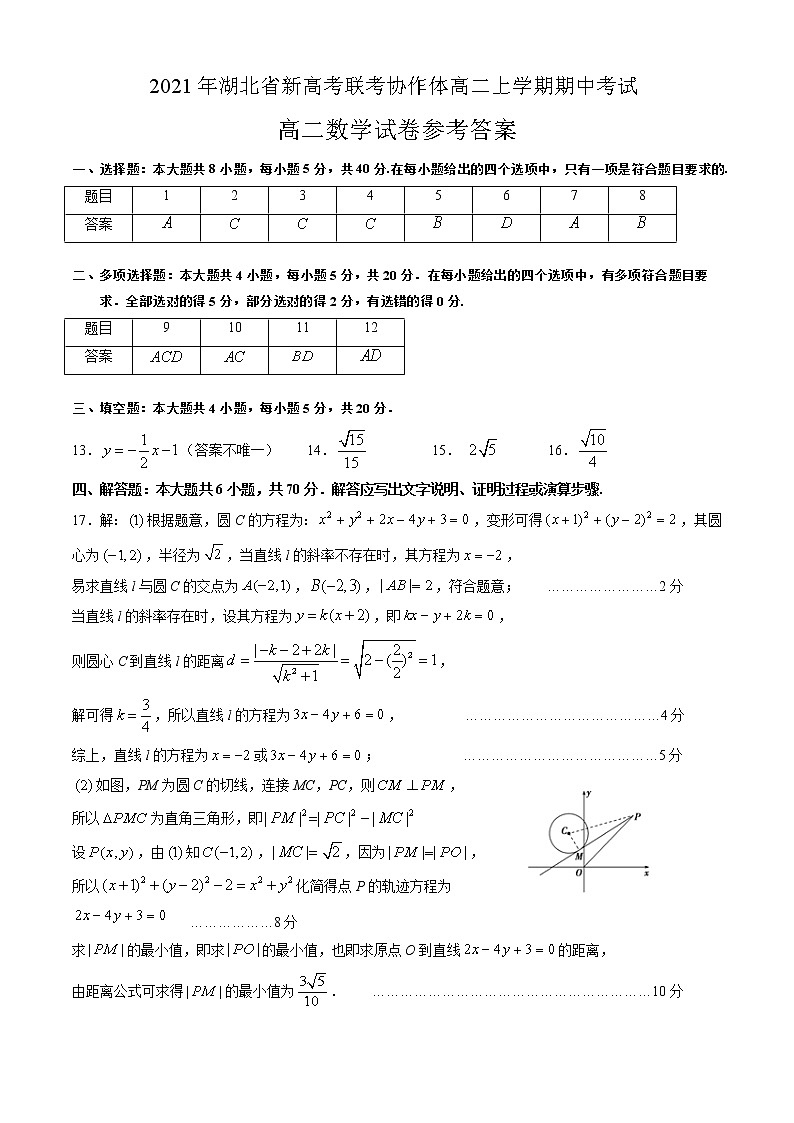
2021年湖北省新高考联考协作体高二上学期期中考试高二数学试卷参考答案一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.题目12345678答案 二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分.题目9101112答案 三、填空题：本大题共4小题，每小题5分，共20分．13．（答案不唯一）    14．         15．        16．     四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.17．解：根据题意，圆C的方程为：，变形可得，其圆心为，半径为，当直线l的斜率不存在时，其方程为，     
易求直线l与圆C的交点为，，，符合题意；    ……………………2分
当直线l的斜率存在时，设其方程为，即，
则圆心C到直线l的距离，解可得，所以直线l的方程为，         ……………………………………4分综上，直线l的方程为或；            ……………………………………5分
如图，PM为圆C的切线，连接MC，PC，则，
所以为直角三角形，即
设，由知，，因为，所以化简得点P的轨迹方程为   ………………8分求的最小值，即求的最小值，也即求原点O到直线的距离，由距离公式可求得的最小值为．    ……………………………………………………10分 18．解：若选①，因为，又由正弦定理可知：，所以，又，则，所以，又，所以；   ………………3分若选②，，由余弦定理得，所以，又且，所以，又，所以；    …………………3分若选③，由展开得，又由正弦定理可知，在中，，所以，又，则，所以，所以，可得.又，所以，所以，所以；  ……………………3分 （1）解法一：若，由正弦定理得，又，所以，可得，所以，……………………5分又，所以，所以，又，所以，所以；       ……………………………7分解法二：若，又，由余弦定理可知，即，整理得，解得或，                                 ………………………………………5分若，，则，与矛盾；    ………………………………………6分若，则，由余弦定理可得； …………………………7分（2）由，及正弦定理知．由，所以，      …………………………………9分又由余弦定理得，即，整理可得，，可得，所以．       ………………………………12分 19．解：（1）证明：平面ABCD，平面ABCD，，，为正三角形，四边形ABCD是菱形，，         ………………………2分
又，PD，平面PBD，平面PBD，        ………………………4分    
而平面EAC，平面平面．                     ………………………5分（2）解：如图，连接OE，由可知平面PBD，平面PBD，
，又，
即为二面角的平面角。      ……………………7分
过E作，交BD于点H，则，
，，          ……………………8分  
正中，，，， …………………………10分
在中，，，
即二面角的大小为．（注：用其它方法应按相应步骤给分）     ………………12分 20．解：组距为，由，得                       …………………………………………………2分各组的组中值和相应的频率依次为：组中值3035404550频率所以，        ………………4分
    ………………7分
由已知，抽取的40个果实中，重量在和内的分别有4个和3个，
分别记为，，，和，，，         ……………………………………………9分
从中任取2个的取法有：，，，，，，，，，，，，，，，，，，，，，共21种取法，其中都是优质果实的取法有，，，共3种取法，
所以抽到的都是优质果实的概率          ……………………………………………12分                   21．解：由题知，且，分别以所在直线为轴建立空间直角坐标系，则点        …………………2分（1），设平面的法向量为，则，得，得，当时，得                ……………………………………4分同理可得平面的一个法向量为            ……………………………………5分 那么，所以二面角的余弦值为  …………7分 （2）假设在线段上存在一点，使平面，设，则由，得，得       …………………………………9分那么，当平面时，，即存在实数，使，解得，     …………………………11分那么，即点是线段的中点时，平面．  ……………………12分  22．解：（1）因为，所以，又，所以，所以，所以椭圆C的标准方程为．      ………………………………3分（2）①当AB的斜率为0时，显然．       ………………………………4分当AB的斜率不为0时，设，由得，设，故有，   ………………………………5分所以．因为，所以．综上所述，恒有为定值．                           ………………………………7分②，        ………………………………9分即==，当且仅当，即时取等号（此时适合），所以面积的最大值为．                       ……………………………………12分