

还剩17页未读,
继续阅读
所属成套资源:苏科版数学七年级下册全册同步课件
成套系列资料,整套一键下载
2021学年9.3 多项式乘多项式备课课件ppt
展开
这是一份2021学年9.3 多项式乘多项式备课课件ppt,共25页。PPT课件主要包含了回顾与思考,+mb,+na,+nb,a+bm+n,+an,+bm,+bn,x2y,xy2等内容,欢迎下载使用。
1.理解和掌握单项式与多项式乘法法则及其推导过程。2.熟练运用法则进行单项式与多项式的乘法计算。3.通过用文字概括法则,提高学生数学表达能力。4.通过反馈练习,培养学生计算能力和综合运用知识的能力。5.渗透公式恒等变形的和谐美、简洁美。
1.利用单项式与多项式相乘的法则推导本节法则。
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项,
进行单项式与多项式乘法运算时,要注意什么?
即单项式要乘遍多项式的每一项.
② 去括号时注意符号的确定.
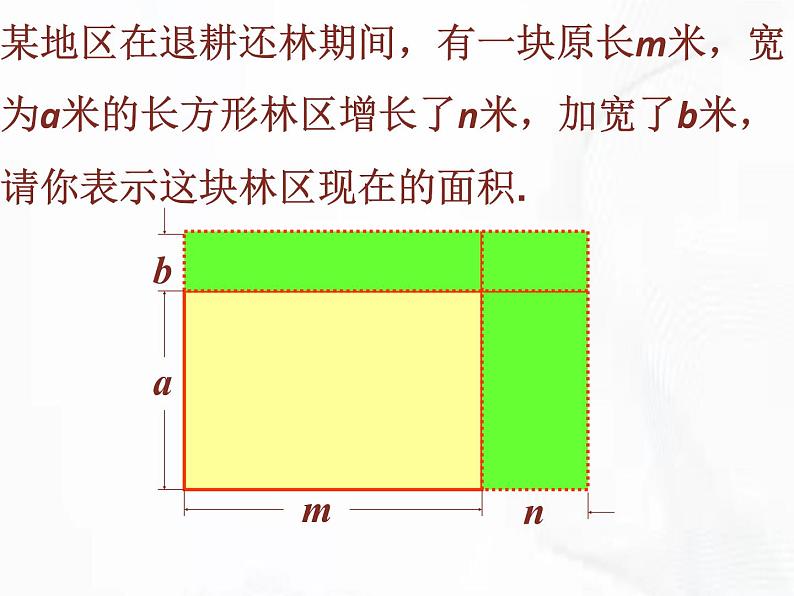
某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区增长了n米,加宽了b米,请你表示这块林区现在的面积.
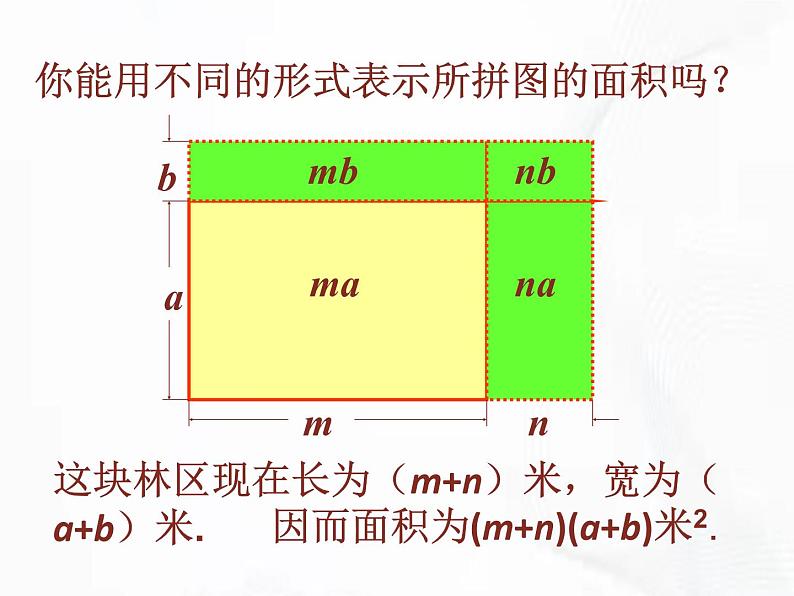
你能用不同的形式表示所拼图的面积吗?
这块林区现在长为(m+n)米,宽为(a+b)米.
因而面积为(m+n)(a+b)米2.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
如何进行多项式与多项式相乘的运算?
例1 计算:(1)(x+2)(x-3);(2)(3x-1)(x-2).
例2 计算:(1)(3m+n)(m-2n);(2)n(n+1)(n+2).
(x+y )( x2-xy+y2)
(1)(x−3y)(x+7y), (2)(2x + 5y)(3x−2y).
x2 +4xy-21y2;
(2) (2x +5 y)(3x−2y)
6x2 +11xy-10y2.
(1) (m+2n)(m−2n); (2) (2n +5)(n−3) ;
(3) (x+2y)2 ; (4) (ax+b)(cx+d ) .
(1) (x+5)(x–7) (2) (2a+3b) (2a+3b)(3) (x+5y)(x–7y)(4) (2m+3n)(2m–3n)
观察上面四个等式,你能发现什么规律?
你能根据这个规律解决下面的问题吗?
计算(3x+y)(x-2y)的值.
拆分成多各单项式:(3x,y)(x,-2y)
按法则算得:3x·x,3x·(-2y),y·x,y·(-2y)
积相加得:3x·x+3x·(-2y)+y·x+y·(-2y)
解:(3x+y)(x-2y)=3x2-6xy+xy-2y2
=3x2-5xy-2y2.
(1)(x+y)(x-y);
解:(x+y)(x-y)=x·x+x·(-y)+y·x+y·(-y)
拆分成多各单项式:(x,y)(x,-y)
按法则算得:x·x,x·(-y),y·x,y·(-y)
积相加得:x·x+x·(-y)+y·x+y·(-y)
拆分成多各单项式:(2a,b)(2a,b)
按法则算得:2a·2a,2a·b,b·2a,b·b
积相加得:2a·2a+2a·b+b·2a+b·b
(2)(2a+b)2;
解:(2a+b)2=2a·2a+2a·b+b·2a+b·b
=4a2+4ab+b2
拆分成多各单项式:(x,y)(x2,-xy,y2)
按法则算得:x·x2,x·(-xy),x·y2,y·x2,
积相加得:x·x2+x·(-xy)+x·y2+y·x2+y·(-xy)+y·y2
(3)(x+y)(x2-xy+y2).
解:(x+y)(x2-xy+y2)
y·(-xy),y·y2
=x3-x2y+xy2+x2y-xy2+y3
=x·x2+x·(-xy)+x·y2+y·x2+y·(-xy)+y·y2
由上面计算的结果找规律,观察下图,填空:
如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值.
解:原式= x4 – 3x3 + c x2 +bx3 – 3bx2 +bcx+8x2– 24x+8c
x2项系数为:c –3b+8
x3项系数为:b – 3
∴ b=3 , c=1.
1.理解和掌握单项式与多项式乘法法则及其推导过程。2.熟练运用法则进行单项式与多项式的乘法计算。3.通过用文字概括法则,提高学生数学表达能力。4.通过反馈练习,培养学生计算能力和综合运用知识的能力。5.渗透公式恒等变形的和谐美、简洁美。
1.利用单项式与多项式相乘的法则推导本节法则。
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项,
进行单项式与多项式乘法运算时,要注意什么?
即单项式要乘遍多项式的每一项.
② 去括号时注意符号的确定.
某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区增长了n米,加宽了b米,请你表示这块林区现在的面积.
你能用不同的形式表示所拼图的面积吗?
这块林区现在长为(m+n)米,宽为(a+b)米.
因而面积为(m+n)(a+b)米2.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
如何进行多项式与多项式相乘的运算?
例1 计算:(1)(x+2)(x-3);(2)(3x-1)(x-2).
例2 计算:(1)(3m+n)(m-2n);(2)n(n+1)(n+2).
(x+y )( x2-xy+y2)
(1)(x−3y)(x+7y), (2)(2x + 5y)(3x−2y).
x2 +4xy-21y2;
(2) (2x +5 y)(3x−2y)
6x2 +11xy-10y2.
(1) (m+2n)(m−2n); (2) (2n +5)(n−3) ;
(3) (x+2y)2 ; (4) (ax+b)(cx+d ) .
(1) (x+5)(x–7) (2) (2a+3b) (2a+3b)(3) (x+5y)(x–7y)(4) (2m+3n)(2m–3n)
观察上面四个等式,你能发现什么规律?
你能根据这个规律解决下面的问题吗?
计算(3x+y)(x-2y)的值.
拆分成多各单项式:(3x,y)(x,-2y)
按法则算得:3x·x,3x·(-2y),y·x,y·(-2y)
积相加得:3x·x+3x·(-2y)+y·x+y·(-2y)
解:(3x+y)(x-2y)=3x2-6xy+xy-2y2
=3x2-5xy-2y2.
(1)(x+y)(x-y);
解:(x+y)(x-y)=x·x+x·(-y)+y·x+y·(-y)
拆分成多各单项式:(x,y)(x,-y)
按法则算得:x·x,x·(-y),y·x,y·(-y)
积相加得:x·x+x·(-y)+y·x+y·(-y)
拆分成多各单项式:(2a,b)(2a,b)
按法则算得:2a·2a,2a·b,b·2a,b·b
积相加得:2a·2a+2a·b+b·2a+b·b
(2)(2a+b)2;
解:(2a+b)2=2a·2a+2a·b+b·2a+b·b
=4a2+4ab+b2
拆分成多各单项式:(x,y)(x2,-xy,y2)
按法则算得:x·x2,x·(-xy),x·y2,y·x2,
积相加得:x·x2+x·(-xy)+x·y2+y·x2+y·(-xy)+y·y2
(3)(x+y)(x2-xy+y2).
解:(x+y)(x2-xy+y2)
y·(-xy),y·y2
=x3-x2y+xy2+x2y-xy2+y3
=x·x2+x·(-xy)+x·y2+y·x2+y·(-xy)+y·y2
由上面计算的结果找规律,观察下图,填空:
如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值.
解:原式= x4 – 3x3 + c x2 +bx3 – 3bx2 +bcx+8x2– 24x+8c
x2项系数为:c –3b+8
x3项系数为:b – 3
∴ b=3 , c=1.