2020-2021学年第12章 证明12.2 证明备课课件ppt

这是一份2020-2021学年第12章 证明12.2 证明备课课件ppt，共39页。PPT课件主要包含了图12-1，试一试，图12-3，图12-4，图12-5，第一步，画出图形，第二步，写出证明过程，第三步等内容，欢迎下载使用。

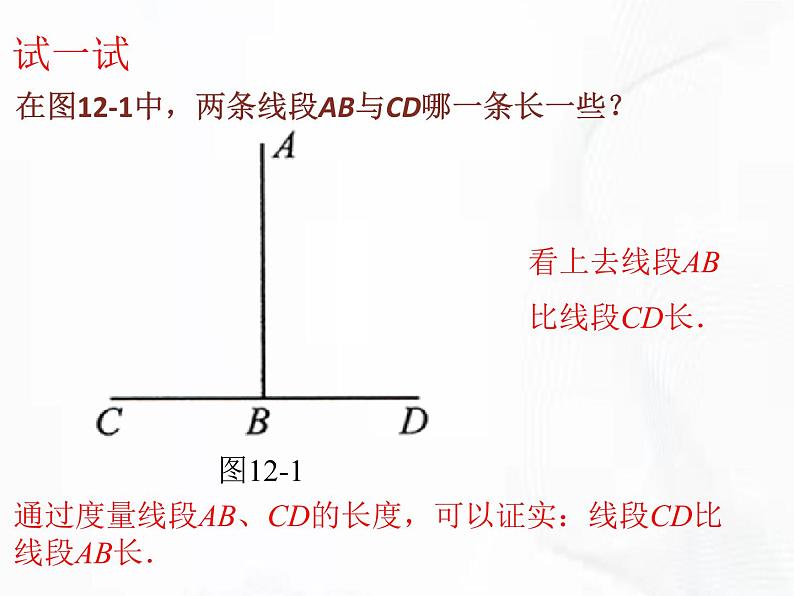
在图12-1中，两条线段AB与CD哪一条长一些？
看上去线段AB比线段CD长．
通过度量线段AB、CD的长度，可以证实：线段CD比线段AB长．
如果将图12-2(2）中小道左边的草坪向右平移1m，那么得到一个长为（a-1)m、宽为bm的长方形（如图12-3)，它的面积为b(a-1)m2.于是，“曲径”的面积为ab-b(a-1)=ab-ab+b=b(m2).由图12-2(1）可知直道的面积为1×b=b(m2).
通过图形的平移和计算，可以证实：两条小道的面积等．
1．图12-4(l）是一张8×8的正方形纸片，把它剪成4块，按图12-4(2）重新拼合.
这4块纸片恰好能拼成一个长为13、宽为5的长方形吗？
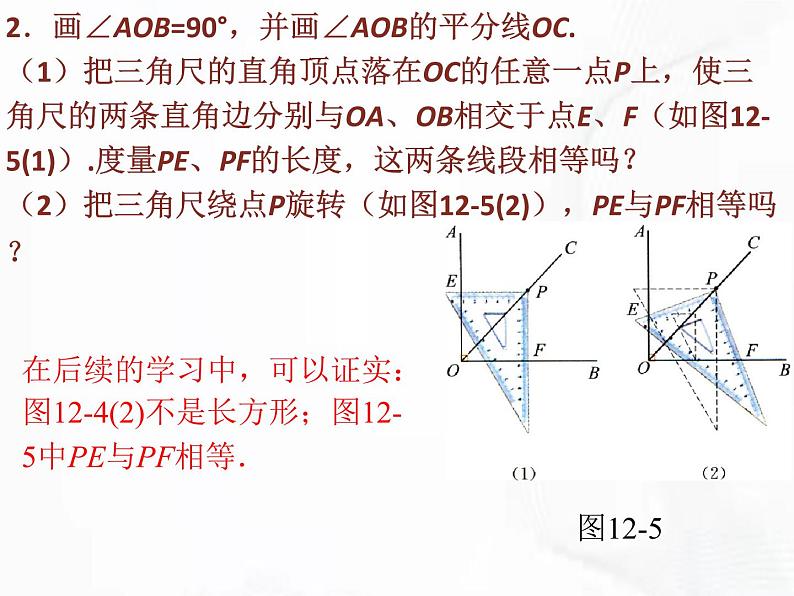
2．画∠AOB=90°，并画∠AOB的平分线OC.（1）把三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边分别与OA、OB相交于点E、F（如图12-5(1)）.度量PE、PF的长度，这两条线段相等吗？（2）把三角尺绕点P旋转（如图12-5(2)），PE与PF相等吗？
在后续的学习中，可以证实：图12-4(2)不是长方形；图12-5中PE与PF相等．
命题，有真命题，也有假命题.要说明一个命题是假命题，只要举出反例即可. 要说明一个命题是真命题，则要从命题的条件出发，根据已学过的基本事实、定义、性质、和定理等，进行有理有据的推理.这种推理的过程叫做证明(prf).经过证明的真命题称为定理（therem).
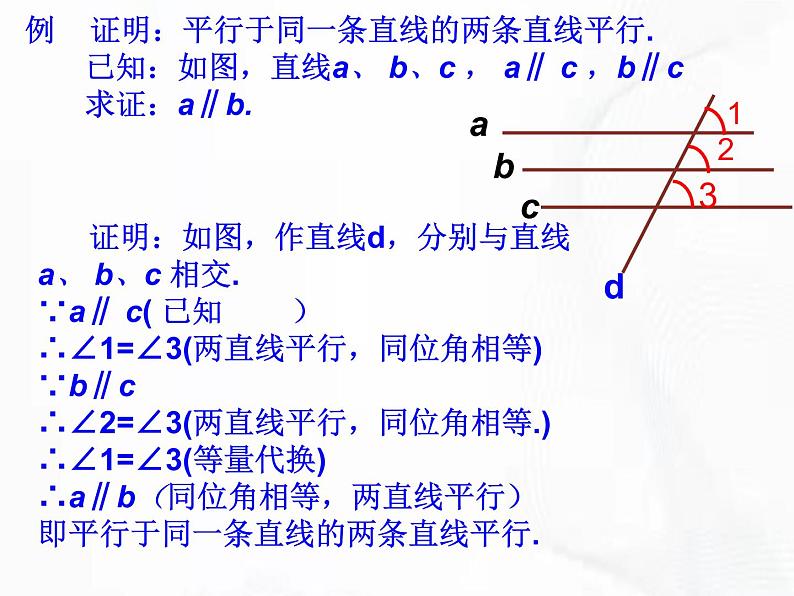
例 证明：平行于同一条直线的两条直线平行. 已知：如图，直线a、 b、c ， a∥ c ，b∥c 求证：a∥b.
证明：如图，作直线d，分别与直线a、 b、c 相交.∵a∥ c( 已知 ）∴∠1=∠3(两直线平行，同位角相等)∵b∥c∴∠2=∠3(两直线平行，同位角相等.)∴∠1=∠3(等量代换)∴a∥b（同位角相等，两直线平行）即平行于同一条直线的两条直线平行.
已知:如图，直线AB和CD相交于点O.求证:∠1=∠2.
同角（或等角）的余角相等
（ ）
　　平行线的性质定理一　两条平行线被第三条直线所截，内错角相等．
1.指出定理的条件和结论，并画出图形，结合图形写出已知、求证．
2. 说说你的证明思路，试着写出证明过程.
例1 已知：如图12-7，直线AB、CD被直线EF所截，AB∥CD，MG平分∠EMB，NH平分∠END.求证：MG∥NH.
证明：∵AB∥CD（已知），∴∠EMB=∠END（两直线平行，同位角相等）.∵MG平分∠EMB，NH平分∠END（已知），∴∠EMG= ∠EMB，∠ENH= ∠END（角平分线的定义）.∴∠EMG=∠ENH（等量代换）.∴MG∥NH（同位角相等，两直线平行）.
例.已知：如图，直线AB、CD与直线EF相交，且∠1=∠2.求证：AB∥CD
证明：∵∠1=∠2 (已知)又∵∠1=∠3(对顶角相等)∴∠2=∠3(等量代换)∴AB∥CD (同位角相等，两直线平行)
例2 已知：如图12-9，AC、BD相交于点O.求证：∠A+ ∠B= ∠C+ ∠D.
证明：在△AOB中， ∠A+ ∠B+ ∠AOB=180 °（三角形三个内角的和等于180 °）.∴ ∠A+ ∠B=180 °-∠AOB（等式性质）.在△COD中，同理可得∠C+ ∠D=180 °-∠COD.∵∠AOB= ∠COD（对顶角相等）.∴ ∠A+ ∠B=∠C+ ∠D（等量代换）.
例.已知：如图，∠AOB=∠BOC=180°， OE平分∠AOB，OF平分∠BOC求证：OE⊥OF
∵OE平分∠AOB，OF平分∠BOC，(已知)∴∠1= ∠AOB，∠2= ∠BOC．(角平分线的定义)又∵∠AOB=∠BOC=180°，(已知)∴∠1+∠2= (∠AOB+∠BOC)=90°．(等式性质)∴OE⊥OF(垂直的定义)
补充完成下列各题的证明，并填上推理的依据.
1.已知：如图，AB∥CD，AD∥BC.求证：∠A=∠C.
证明：∵ AB∥CD，( )∴∠A＋∠D=180°.( )∵ AD∥BC，( )∴ ∠C＋∠D=180°.( )∴ ∠A＋∠D=∠C＋∠D( )∴ ∠A=∠C.( )
两直线平行，同旁内角相等.
两直线平行，同旁内角互补.
证明：∵ DC∥AB ，( )∴ ∠ABD= ∠CDB( )∵ DF平分∠CDB ，BE平分∠ABD.( )∴ ∠1= ∠CDB ，( )∴ ∠2= ∠ABD .( )∴ ∠1=∠2.( )
2.已知：如图，DC∥AB，DF平分∠CDB，BE平分∠ABD.求证：∠1=∠2.
两直线平行，内错角角相等.
三角形三个内角的和等于
已知：△ABC.求证：∠A +∠B +∠C=180°
命题的正确性还要严密的推理证明想一想：如何证明呢？
三角形内角和定理：
(同位角相等，两直线平行).
(两直线平行，内错角相等).
∵B，C，D在同一直线上∴ ∠1+∠2+∠ACB=∠A+∠B+∠ACB=180°
延长BC到D，在△ABC的外部，以CA为一边，CE为另一边作∠2 =∠B，
在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线.在平面几何里，辅助线通常画成虚线.
为了证明三个角的和为1800，可以转化为一个平角，这种转化思想是数学中的常用方法.
　　问题 如图，把△ABC 的一边BC 延长，得到∠ACD．这个角还是三角形的内角吗？
　 概念：　　三角形的一边与另一边的　　　延长线组成的角，叫做三角形的外角．
∠ACD（外角）+ ∠ACB（相邻的内角）=180°．
　　问题 如图，∠ACD 与∠ACB 的位置是怎样的？∠ACD 与∠ACB 有什么数量关系？
如图，∵　∠ACD +∠ACB =180°，　　∠A +∠B +∠ACB =180°，∴　∠ACD =∠A +∠B．
　　问题 如图，∠ACD 与∠A，∠B 的位置是怎样的？∠ACD 与∠A，∠B 的大小有什么关系？你能证明你的结论吗？
　　三角形内角和定理的推论： 三角形的一个外角等于与它不相邻的两个内角的和． 三角形的外角大于与它不相邻的任何一个内角．　　推论是由定理直接推出的结论，和定理一样，推论可以作为进一步推理的依据．
一、如图，在长方形ABCD中，横向阴影部分是长方形，另一阴影部分是平形四边形，根据图中标明的数据，计算空白部分的面积？
点拔：这里通过平移，避免了对图形分别计算面积，使求解简洁方便.
析解：利用“平移不改变图形的形状与大小”这一性质可以迅速解决本题.由图可知，四个空白四边形经过平移可以组成一个长方形，它的长为（a-c)，宽为(b-c)，所以空白部分的面积为：（a-c)(b-c)=ab-ac-bc+c2
　如图的图案是一个轴对称图形（不考虑颜色），直线l 是它的一条对称轴.已知图中圆的半径为r，求绿色部分的面积.
　　解：如果以直线l为对称轴，把l左边绿色部分反射到l的右边，那么它们的像恰好填补了右边白色部分．所以图中的绿色部分的面积等于半圆的面积是 .
画一个腰长等于3的等腰直角三角形ABC，取一个锐角为45°的三角尺，把三角尺的直角顶点放在Rt△ABC的斜边BC的中点O处，并使三角尺的一条直角边经过点A，另一条直角边经过点B (1).将三角尺绕点O按顺时针方向旋转一个角度，记三角尺的两腰AB，AC的交点分别为E，F(2).在三角尺按图4-27所示的方式绕点O旋转的过程中，线段AE与CF的长度有什么关系？OE与OF的长度有什么关系？证明你的结论.
解：AE=CF，OE=OF.证明如下：连接AO，在△AEO和△CFO中，∵ △ABC是等腰直角三角形，AO⊥BC，垂足为点O，∴ ∠EAO= ∠C=45 °，AO=OC，∠EOA=∠COF=90°-∠AOF，∴ △AEO ≌ △CFO(ASA)∴AE=CF,OE=OF.
1．下列推理是否正确？为什么？
同位角相等，两直线平行．
∵∠4+∠5=180°，
同旁内角互补，两直线平行．
内错角相等，两直线平行．
∵∠3+∠6=180°，
2．如图，已知直线b⊥a，c⊥a，那么直线b与c平行吗？如果平行，请给出证明；如果不平行，请举出反例．
∴b//c．（同位角相等，两直线平行）
1.在下列解答中，填上适当的理由：
（1）∵∠B=∠1（已知）， ∴AD∥BC.
（2）∵∠D=∠1（已知）， ∴AB∥CD.
（同位角相等，两直线平行）
（内错角相等，两直线平行）
2.在下列解答中，填空：
（1）∵∠BAD+∠ABC=180°（已知）， ∴（ ）∥（ ）（ 同旁内角互补，两直线平行 ）.
（2）∵∠BCD+∠ABC=180°（已知）， ∴（ ）∥（ ）（ 同旁内角互补，两直线平行 ）.
3． 根据图中给出的条件，指出互相平行的直线和互相垂直的直线．
相互平行的直线有：c与d；a与b．
相互垂直的直线有：a与e，e与b．
1.根据题意，画出图形;
2.分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论.
3.在“证明”中写出推理过程.且每一步推理都要有依据
证明几何命题的一般格式：