






苏科版七年级下册12.3 互逆命题教学演示课件ppt
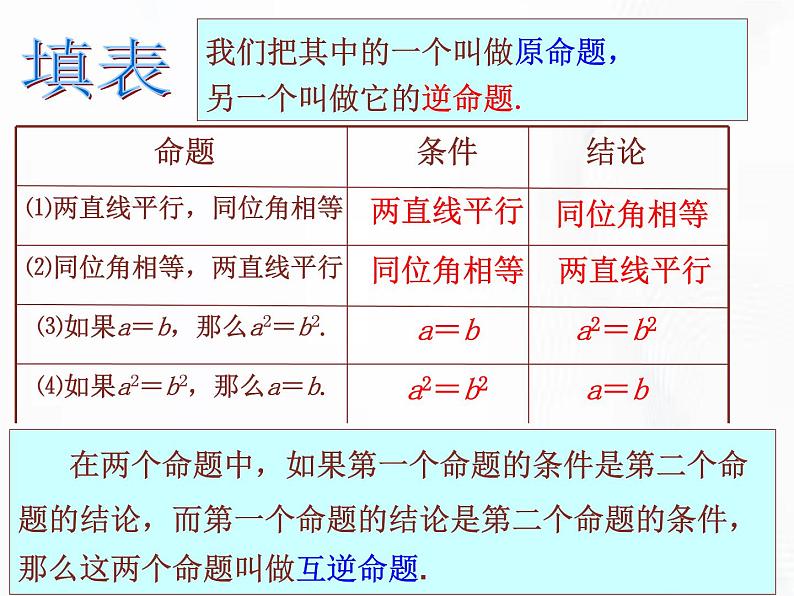
展开⑷如果a2=b2,那么a=b.
⑶如果a=b,那么a2=b2.
⑵同位角相等,两直线平行
⑴两直线平行,同位角相等
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
我们把其中的一个叫做原命题,另一个叫做它的逆命题.
说出下列命题的逆命题,并判定原命题与逆命题的真假.
(2)面积相等的三角形全等.
全等三角形的面积相等.
(3)在一个三角形中,等角对等边.
在一个三角形中,等边对等角.
思考:每个命题都有逆命题吗?
真命题的逆命题是真命题吗?
在数学命题中,请举例说出一个原命题是真命题, 逆命题是假命题的例子;
(4)磁悬浮列车是一种高速行驶时不接触地面的交通工具.
高速行驶时不接触地面的交通工具是磁悬浮列车.
下列说法哪些正确,哪些不正确?
(1)每个命题都有逆命题.
(2)假命题没有逆命题.
(3)真命题的逆命题是真命题.
例1 证明:平行于同一条直线的两条直线平行.
已知:如图12-10,直线a、b、c中,b∥a,c∥a.求证:b∥c.
证明:作直线d,使它与直线a、b、c都相交.∵b∥a(已知),∴∠2=∠1(两直线平行,同位角相等).∵c∥a(已知),∴∠3=∠1(两直线平行,同位角相等). ∴∠2=∠3(等量代换).∴b∥c(同位角相等,两直线平行).
例2 证明:直角三角形的两个锐角互余.
已知:如图12-11,在△ABC中,∠C=90°.求证:∠A+∠B=90°.
证明:在△ABC中,∠A+∠B+∠C=180°(三角形三个内角和等于180°).∴∠A+∠B=180°-∠C(等式性质).∵∠C=90°.(已知),∴∠A+∠B=180°-90°(等量代换).即 ∠A+∠B=90°.
⑴任意作一条线段,并画出它的中垂线
⑵线段的中垂线(垂直平分线)有什么性质?
线段垂直平分线上的点到这条线段两个端点的距离相等
⑶请说出它的逆命题,并证明这个逆命题是真命题.
已知:如图,AB是一条线段,P是一点,且PA=PB.
求证:点P在线段AB的垂直平分线上.
解: 这个命题的逆命题是: 到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一性质)
∴PC是AB的垂直平分线.
∴点P在线段AB的垂直平分线上
⑵当点P在线段AB上,结论显然成立;
⑴当点P不在线段AB上时,
显然,上述两个命题可称为互逆命题.
线段垂直平分线性质定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
∵PA=PB∴点P在AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等.
线段垂直平分线性质定理的逆命题:
例、写出命题“等腰三角形底边上的中点到两腰的距离相等”的逆命题,并证明逆命题是真命题.
已知命题:“P是等边三角形ABC内一点.若点P到三边的距离相等,则PA=PB=PC.”证明这个命题,并写出它的逆命题,判断其逆命题成立吗?
举反例说明下列命题是假命题:(1)如果│a│=│b│,那么a=b;(2)任何数的平方大于0;(3)两个锐角的和是钝角;(4)如果一点到线段两端的距离相等,那么这点事这条线段的中点.
(1)取a=-1,b=1,则│a│=│b│=1,而a≠b;则该命题是假命题.
(2)取x=0,则x2=02=0,则该命题是假命题.
(3)取∠A=15,∠B=12,则∠A+ ∠B=27,则该命题是假命题.
(4)取直线外一点a,令到直线的距离相等,但是该点不是线段的中点,则该命题是假命题.
1.(1)如图,AB∥CD,AB、DE相交于点G,∠B=∠D.在下列括号内填写推理的依据:∵AB∥CD(已知)∴∠EGA=∠D( ). 又∵∠B=∠D(已知)∴∠EGA=∠B( ). ∴DE∥BF( ).
两直线平行,同位角相等
同位角相等,两直线平行
(2)上述推理中,应用了哪两个互逆的真命题?
1).两直线平行,同位角相等. 2).同位角相等,两直线平行.
2.(1)已知:如图,在直角三角形ABC中,∠ACB=90˚,D是AB上一点,且∠ACD=∠B.求证:CD⊥AB.
证明:∵ ∠ACD+∠DCB= ∠ACB=90˚, ∠ACD=∠B,∴ ∠DCB+ ∠B =∠ACB=90˚;又∵∠CDA= ∠DCB+ ∠B =90˚,∴ CD⊥AB.
(2)你在(1)的证明过程中应用了哪两个互逆的真命题?
交角为90˚的两条直线垂直;两条直线相互垂直,交角为90˚.
判断下列说法是否正确:
(1)如果原命题是真命题,那么它的逆命题也是真命题. ( )(2)如果原命题是假命题,那么它的逆命题也是假命题. ( )(3)每个命题都有逆命题. ( )(4)“面积相等的两个三角形是全等三角形”与“面积不相等的两个三角形不是全等三角形”是一对互逆命题 . ( )
1.如图,已知∠1=∠2,∠3=∠4,∠E=90°.求证:AB∥CD.
证明:∵ ∠1=∠2,∠3=∠4,∠E=90°.(已知)∴∠1+∠3=∠2+∠4=90°.(三角形内角和等于180°)∴∠BAC+∠ACD=180°.(已求)∴ AB∥CD.(同旁内角互补,两直线平行)
2.如图,在△ABC中,∠B=∠C,D是BC边上的一点.过点D作DF⊥BC,DE⊥AB,垂足分别为点F,E.求证:∠FDE=∠C .
证明:∵ ∠B=∠C, DF⊥BC,DE⊥AB.∴∠EDB=∠CFD,(同角的余角相等)∴∠C+∠CFD=∠C+∠EDB=∠EDF+∠EDB=90°.∴∠FDE=∠C .
七年级下册第12章 证明12.3 互逆命题习题课件ppt: 这是一份七年级下册第12章 证明12.3 互逆命题习题课件ppt,共11页。
苏科版12.3 互逆命题背景图ppt课件: 这是一份苏科版12.3 互逆命题背景图ppt课件,文件包含123互逆命题ppt、123互逆命题doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
初中苏科版12.3 互逆命题多媒体教学ppt课件: 这是一份初中苏科版12.3 互逆命题多媒体教学ppt课件,共28页。PPT课件主要包含了命题的概念,命题都有两部分,题设和结论,练习3,原命题,逆命题,假命题,真命题,相等的角是内错角等内容,欢迎下载使用。













