






初中数学人教版八年级下册17.2 勾股定理的逆定理课文内容课件ppt
展开第十七章 勾股定理
17.2 勾股定理的逆定理
第2课时 勾股定理的逆定理(2)
一、 教学目标
1.理解并掌握证明勾股定理的逆定理的方法.
2.理解逆定理、互逆定理的概念.
二、 重点难点
重点
勾股定理的逆定理的证明及互逆定理的概念.
难点
理解互逆定理的概念.
三、 教学设计
(一) 新知导入
问题1 我们学过的勾股定理的内容是什么?
如果直角三角形的两条直角边长分别为a,b,斜边长为c,
那么a2+b2=c2.
问题2 勾股定理的逆定理的内容是什么?
如果三角形的三边长a,b,c 满足a2+b2=c2,
那么这个三角形是直角三角形.
1、判断由线段a、b、c组成的三角形是不是直角三角形:
(1)a=7,b=24,c=25; (2)a= ,b=4,c=5;
解:(1)因为a2+b2=49+576=625, c2=252=625
a2+b2=c2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
(2)因为b2+c2=16+25=41, a2=41
b2+c2=a2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
(3)a= ,b= 1,c= (4)a=40,b=50,c=60.
解:(3)因为c2+b2=
, a2=
c2+b2=a2
所以,根据勾股定理的逆定理,a、b、c组成的三角形是直角三角形
(4)因为a2+b2=1600+2500=4100, c2=3600 , a2+b2≠c2
所以,根据勾股定理的逆定理,a、b、c组成的三角形不是直角三角形
(二) 新知讲解
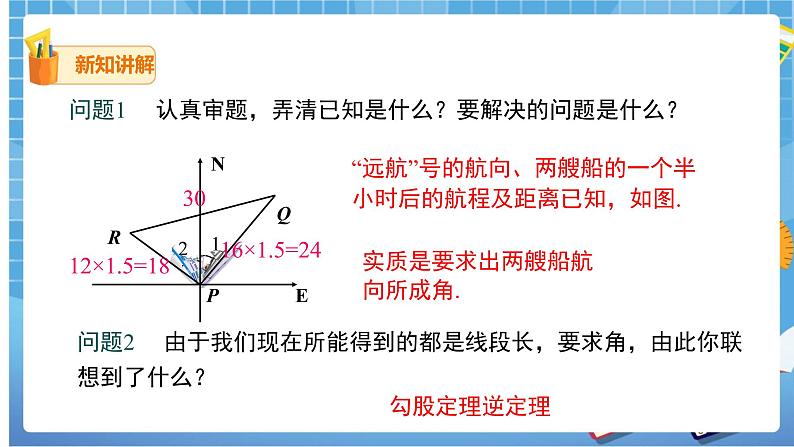
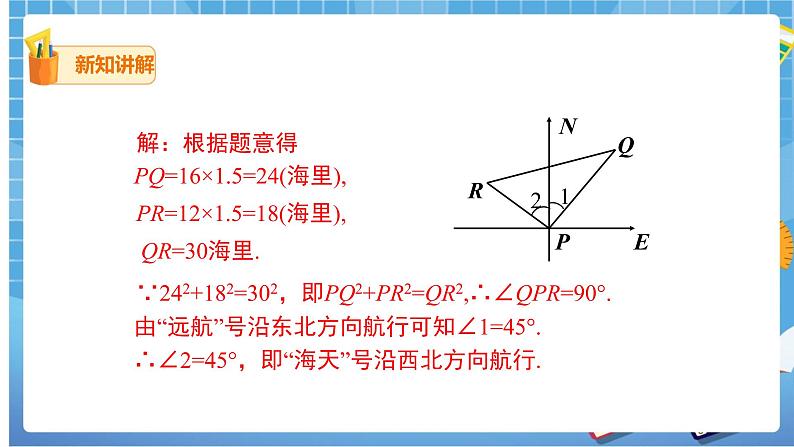
(三) 例1 如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
问题1 认真审题,弄清已知是什么?要解决的问题是什么?
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如图.
实质是要求出两艘船航
向所成角.
问题2 由于我们现在所能得到的都是线段长,要求角,由此你联想到了什么?
勾股定理逆定理
解决实际问题的步骤:
构建几何模型(从整体到局部);
标注有用信息,明确已知和所求;
应用数学知识求解.
例2 如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
解析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
四边形问题对角线是常用的辅助线,它把四边形问题转化成两个三角形的问题.在使用勾股定理的逆定理解决问题时,它与勾股定理是“黄金搭挡”,经常配套使用.
1.A、B、C三地的两两距离如图所示,A地在B地的正东方向,C在B地的什么方向?
(四) 课堂练习
1. 医院、公园和超市的平面示意图如图所示,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的北偏东 的方向.
(五) 拓展提高
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
四、 课堂总结
(1)通过本节课的学习,我们更加明确了勾股定理及
其逆定理的用途及用法,你能说说吗?
(2)通过对勾股数的研究,你有什么结论?
五、 板书设计
六、作业设计
课后作业:课本34页习题17.2第3题。
初中数学人教版八年级下册17.2 勾股定理的逆定理备课ppt课件: 这是一份初中数学人教版八年级下册17.2 勾股定理的逆定理备课ppt课件,文件包含第2课时勾股定理的逆定理的应用pptx、中国航海日mp4等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
初中数学华师大版八年级下册2. 函数的图象获奖ppt课件: 这是一份初中数学华师大版八年级下册2. 函数的图象获奖ppt课件,文件包含华东师大版中学数学八年级下172函数的图象2函数的图象教学课件pptx、1722函数的图象同步练习docx、第17章函数及其图象172函数的图象第2课时docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
人教版八年级下册17.2 勾股定理的逆定理精品ppt课件: 这是一份人教版八年级下册17.2 勾股定理的逆定理精品ppt课件,文件包含172勾股定理的逆定理第2课时勾股定理的逆定理的应用pptx、RJ中学数学八年级下第十七章172勾股定理的逆定理第2课时教学详案docx等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。













