人教版八年级下册第十九章 一次函数19.1 变量与函数19.1.2 函数的图象课文内容课件ppt

第十九章  一次函数

　19.1.2　函数的图象

第1课时　函数的图象

一、 教学目标

准确地运用列表、描点、连线等步骤画出函数的图象

二、 重点难点

重点

函数图象的画法，观察分析图象的信息．

难点

函数图象的理解，概括图象中的信息．

三、 教学设计

（一）   新知导入

（PPT2展示问题和图片）

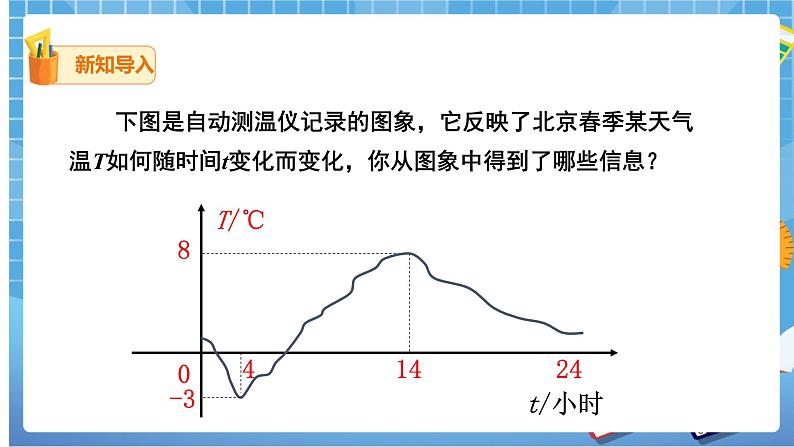
    下图是自动测温仪记录的图象，它反映了北京春季某天气温T如何随时间t变化而变化，你从图象中得到了哪些信息？

（展示PPT3，让学生自由回答）

（展示PPT4，将问题细化，逐个教学生回答，过程中教师做好引导）

(1)最低、最高温度分别是多少？

(2)哪些时段温度呈下降状态？上升状态呢？

(3)我们可以从图象中看出这一天中任一时刻的气温大约是多少吗？

(4)如果长期观察这样的气温图象，我们能总结出气温的变化规律吗？

（二）   新知讲解

（PPT5展示问题1）

问题1  正方形的面积S与边长x的函数解析式为                ，其中x的取值范围是            .

我们还可以利用在坐标系中画图的方法来表示S与x的关系.

（展示PPT6，引导学生分析问题）

(1)在平面直角坐标系中，平面内的点可以用一对               来表示.即坐标平面内         与有序数对是一一           的.

(2)怎样获得组成图形的点？

(3)怎样确定满足函数关系的点的坐标？

(4)自变量x 的一个确定的值与它所对应的唯一的函数值S，是否唯一确定了一个点（x，S）呢？

（展示PPT7，表格和函数图像，此图像没有必要详细讲解，主要通过此图像引出函数图像的概念，详细的函数图像的画法通过后面的例题讲解）

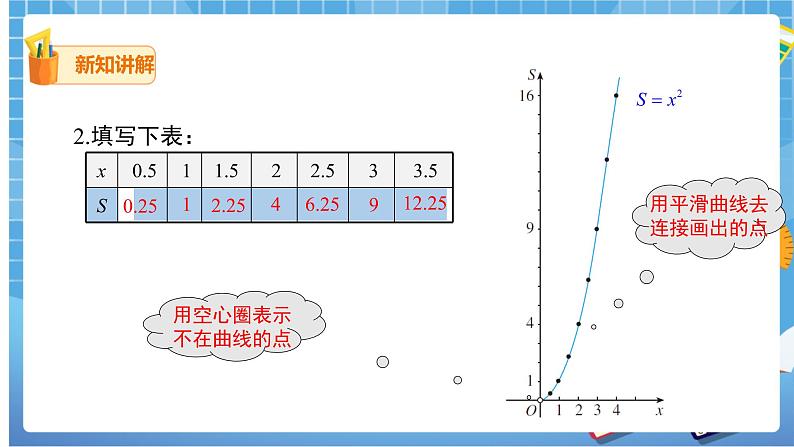
2.填写下表：

（PPT8展示函数图像概念）

　一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．如右图中的曲线就叫函数 （x＞0）的图象．

（PPT9展示例题）

例1 下图反映的过程是小明从家去食堂吃早餐，接着去图书馆读报，然后回家．其中x 表示时间，y 表示小明离家的距离，小明家、食堂、图书馆在同一直线上．

根据图象回答下列问题：

(1)食堂离小明家多远？小明从家到食堂用了多少时间？

（2）小明在食堂吃早餐用了多少时间？

（3）食堂离图书馆多远？小明从食堂到图书馆用了多少时间？

（4）小明读报用了多长时间？

（5）图书馆离小明家多远？小明从图书馆回家的平均速度是多少？

（PPT14展示例题2）

例2  画出下列函数的图象：

     （1）y=x+0.5;

     （2）         .

  解：(1)从函数解析式可以看出，x的取值范围是                 .

 第一步：从x的取值范围中选取一些简洁的数值，

 算出y的对应值，填写在表格里：

第二步：根据表中数值描点（x，y）；

第三步：用平滑曲线连接这些点.

画出的图象是一条     ，

当自变量的值越来越大时，

对应的函数值          .

解：(2)列表 ：取一些自变量的值，并求出对应的函数值，填入表中.

(2)描点： 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.

(3)连线： 用光滑的曲线把这些点依次连接起来.

（PPT18展示画函数图像的一般步骤）

归纳总结

画函数图象的一般步骤：

第一步，列表——表中给出一些自变量的值及

其                ；

第二步，描点——在平面直角坐标系中，以自

变量的值为       ，相应的函数值为       ，描出表格中数值对应的各点；

第三步：连线——按照横坐标           的顺序，

把所描出的各点用           连接起来.

　　（展示PPT19，承上启下，引出下一个问题）

我们知道，函数图象是以自变量的值和对应的函数值分别为横、纵坐标的点组成的图形，这样的点有无数个，那么怎样判断一个点是否在函数图象上？

（展示PPT20，阐述清楚如何判断一个点是否在函数图像是）

（三）   课堂练习

    1、 中，对于x的每一个确定的值，y都有唯一的对应值，

即y是x的函数.画出这个函数的图象：

解：（1）从函数解析式可以看出，x的取值范围是：              

第一步：从x的取值范围中选取一些简洁的数值，算出y的对应值，填写在

表格里：

第二步：根据表中数值描点（x，y）；

第三步：用平滑曲线连接这些点.

画出的图象是一条     ，

　当自变量的值越来越大时，对应的函数值          .

2、下图是自动测温仪记录的图象，它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化．你从图象中得到了哪些信息？

（1）从这个函数图象可知：这一天中                        气温最低（           ）,          气温最高（          ）

（2）从_     __至           气温呈下降状态，从4时至 14时气温呈上升状态，从           至           气温又呈下降状态.

（3）我们可以从图象中看出这一天中任一时刻的气温大约是多少.

（四）   拓展提高

1、画出函数的图象；

2、从图象中观察，当x＜0时，y随x的增大而增大，还是y随x的增大而减小?当x＞0时呢？

  .

四、 课堂总结

（1）函数图象会使函数关系更为清晰，怎样画出函数的图象呢？

（2）如何根据函数图象中获得的信息来研究实际问题？

（3）画函数图象的三个步骤分别是什么？

（4）如何从图象中了解函数的变化情况？

五、 板书设计

六、作业设计

　　　　　　　　　　　　　　　课后作业：课本82页习题第6题。