初中数学北师大版九年级下册1 二次函数完美版ppt课件

这是一份初中数学北师大版九年级下册1 二次函数完美版ppt课件，文件包含21二次函数PPTpptx、21二次函数教学设计doc等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。
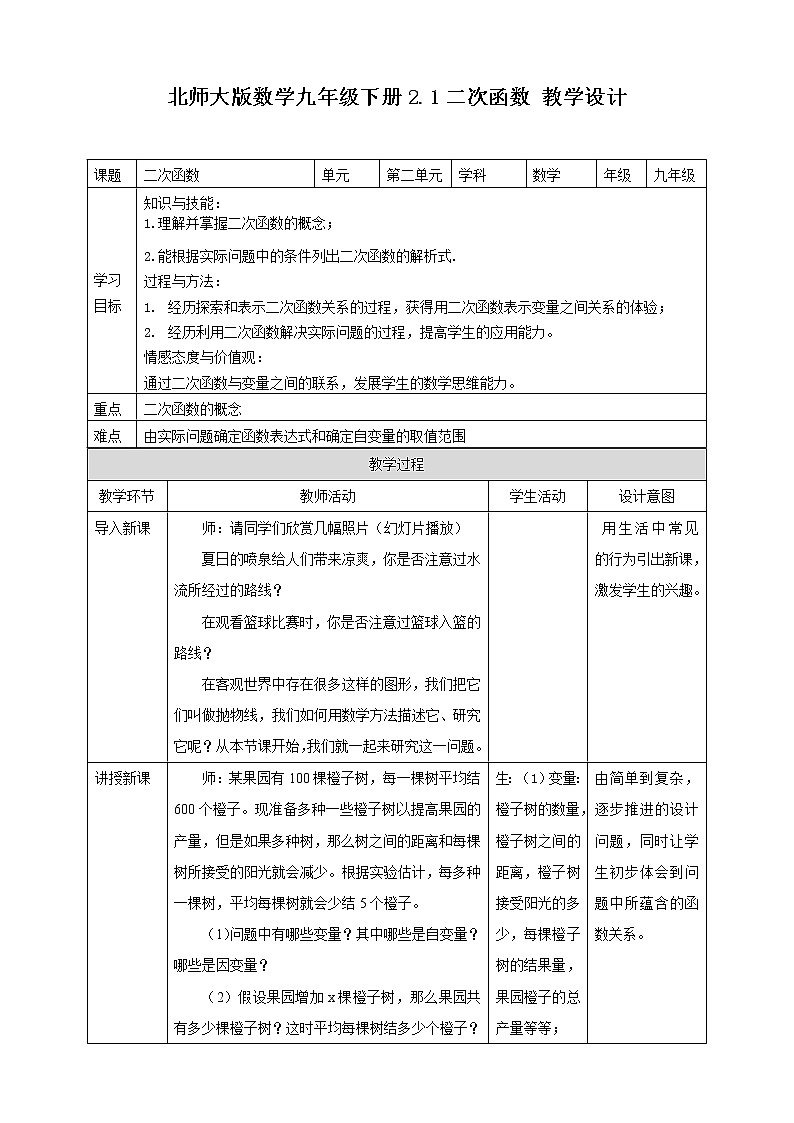
北师大版数学九年级下册2.1二次函数 教学设计 课题 二次函数单元第二单元学科数学年级九年级学习目标知识与技能：1.理解并掌握二次函数的概念； 2.能根据实际问题中的条件列出二次函数的解析式.过程与方法：经历探索和表示二次函数关系的过程，获得用二次函数表示变量之间关系的体验；经历利用二次函数解决实际问题的过程，提高学生的应用能力。情感态度与价值观：通过二次函数与变量之间的联系，发展学生的数学思维能力。重点二次函数的概念难点由实际问题确定函数表达式和确定自变量的取值范围 教学过程教学环节教师活动学生活动设计意图导入新课师：请同学们欣赏几幅照片（幻灯片播放）夏日的喷泉给人们带来凉爽，你是否注意过水流所经过的路线？ 在观看篮球比赛时，你是否注意过篮球入篮的路线？在客观世界中存在很多这样的图形，我们把它们叫做抛物线，我们如何用数学方法描述它、研究它呢？从本节课开始，我们就一起来研究这一问题。   用生活中常见的行为引出新课，激发学生的兴趣。讲授新课师：某果园有100棵橙子树，每一棵树平均结600个橙子。现准备多种一些橙子树以提高果园的产量，但是如果多种树，那么树之间的距离和每棵树所接受的阳光就会减少。根据实验估计，每多种一棵树，平均每棵树就会少结5个橙子。（1）问题中有哪些变量？其中哪些是自变量？哪些是因变量？（2）假设果园增加x棵橙子树，那么果园共有多少棵橙子树？这时平均每棵树结多少个橙子？（3）如果果园橙子的总产量y个，那么请你写出y与x之间的关系式。              师：银行的储蓄利率是随时间的变化而变化的，也就是说，利率是一个变量。在我国，利率的调整是由中国人民银行根据国民经济发展的情况而决定的。设人民币一年定期储蓄的年利率是x，一年到期后，银行将本金和利息自动按一年定期储蓄转存。如果存款额是100元，那么请你写出两年后的本息和y（元）的表达式（不考虑利息税）。想一想：(1)已知矩形的周长为40cm，它的面积可能是100cm2吗？可能是75 cm2吗？还可能是多少？你能表示这个矩形的面积与其一边长的关系吗？解：设其中一边为xcm,面积为ycm2，则y= x(20-x)=－x2+20x (2)两数的和是20，设其中一个数是x，你能写出这两数之积y的表达式吗？解： y= x(20-x)=－x2+20x师：我们刚才推导出来的关系式 y=100x2+200x+100中分析出y是x的函数，你能说出它的结构特点吗？  师，你能归纳出二次函数的定义吗？它的一般表达式是怎样的？     师：为什么 a≠ 0？    概念中的b和c可以为0吗？表达式应该怎么写？它们还是二次函数吗？       师：根据刚才我们分析得到的，我们总结出关于二次函数应该注意：（1）关于x的代数式一定是整式，a,b,c是常数，且a≠ 0.（2）等式的右边最高次数为2，可以没有一次项和常数项，但不能没有二次项。（3）判断一个函数是不是二次函数，先把它化成一般形式。师：函数y = ax2 + bx + c（ a， b， c 是常数），当a， b， c 满足什么条件时:（1）       它是二次函数？（2）       它是一次函数？（3）       它是正比例函数？师：同学们回答的非常正确，下面我们来检验一下大家的掌握情况。1.下列函数中（ x， t 是自变量）， 哪些是二次函数？y = -12+ 3x2， y = 12x2- x3+ 25， y = 22 + 2x， s = 1 + t + 5t2．2． 圆的半径是 1 cm， 假设半径增加 x cm 时， 圆的面积增加 y cm2．（ 1） 写出 y 与 x 之间的关系式；（ 2） 当圆的半径分别增加 1 cm， cm， 2 cm 时， 圆的面积各增加多少？3. m取何值时，函数y=(m+1)xm2-2m-1+(m-3)x+m是二次函数？4.对于y=(m+3)xm2-7（1）m取什么值时，此函数是正比例函数？（2） m取什么值时，此函数是反比例函数？（3） m取什么值时，此函数是二次函数？4.某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满。当每个房间每天的房价每增加10元时，就会有一个房间空余。宾馆需对游客居住的每个房间每天支出20元的各种费用。根据规定，每个房间的房价每天不得高于340元。设每个房间的房价每天增加x元（x为10的整数倍）。（1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；（2）设宾馆一天的利润为w元，求w与x的函数关系式；生：（1）变量：橙子树的数量，橙子树之间的距离，橙子树接受阳光的多少，每棵橙子树的结果量，果园橙子的总产量等等；自变量：橙子树的数量，橙子树之间的距离等等；因变量：每棵橙子树的结果量，果园橙子的总产量。（2）（100+x）；（600-5x）。（3）果园橙子的总产量y =（ 600 - 5x）（ 100 + x） = -5x2 + 100x + 60000生：y=100(1+x)+100(1+x)xy=100(1+x)2y=100x2+200x+100  生：y关于x的代数式是整式且等式的右边最高次数为2生：一般地，形如y = ax2 + bx + c（ a， b， c 是常数， a≠ 0） 的函数叫做 x 的二次函数 。生：若 a≠ 0，就没有二次项了，就不是二次函数了。生：可以当b=0时， y = ax2 + c当c=0时， y = ax2 + bx 当b=0，c=0时， y = ax2它们都是二次函数。        生：（1）a≠ 0     （2） a=0， b≠ 0 （3） a=0， b≠ 0 ， c =0    生：完成相应练习题由简单到复杂，逐步推进的设计问题，同时让学生初步体会到问题中所蕴含的函数关系。                    通过交流讨论，培养学生思维的严密性和灵活性，让学生体验在交流中收益的乐趣。增强自信心，锻炼学生的语言表达能力。     培养学生分析、比较、归纳的能力。       让学生从丰富的背景中体会函数模型的意义，在大量模型的基础上归纳出二次函数的基本形式                       通过练习巩固新知      课堂小结  板书二次函数一、二次函数的定义y = ax2 + bx + c（ a， b， c 是常数， a≠ 0） 注意：（1）关于x的代数式整式，a≠ 0.（2）等式的右边最高次数为2（3）先函数化成一般形式，再判断是不是二次函数。二、二次函数的特殊形式当b=0时， y = ax2 + c当c=0时， y = ax2 + bx 当b=0，c=0时， y = ax2函数y = ax2 + bx + c（ a， b， c 是常数），（1）a≠ 0时它是二次函数；（2）a=0， b≠ 0时它是一次函数；（3）a=0， b≠ 0 ， c =0它是正比例函数。