初中数学北师大版九年级下册6 直线与圆的位置关系优质ppt课件

课题：3.6直线和圆的位置关系      课型：新授课           年级：九年级

教学目标：

    1．能判断一条直线是否为圆的切线，会过圆上一点画圆的切线．

2．运用切线的判定定理构造直角三角形解决有关问题．

3．会作三角形的内切圆．

教学重点和难点：

重点：1.探索圆的切线的判定方法，并能运用．

      2.作三角形内切圆的方法．

难点：探索圆的切线的判定方法．

教学准备：

教师准备：多媒体课件

学生准备：圆规、直尺

教学过程：

一、复习回顾，引入新课

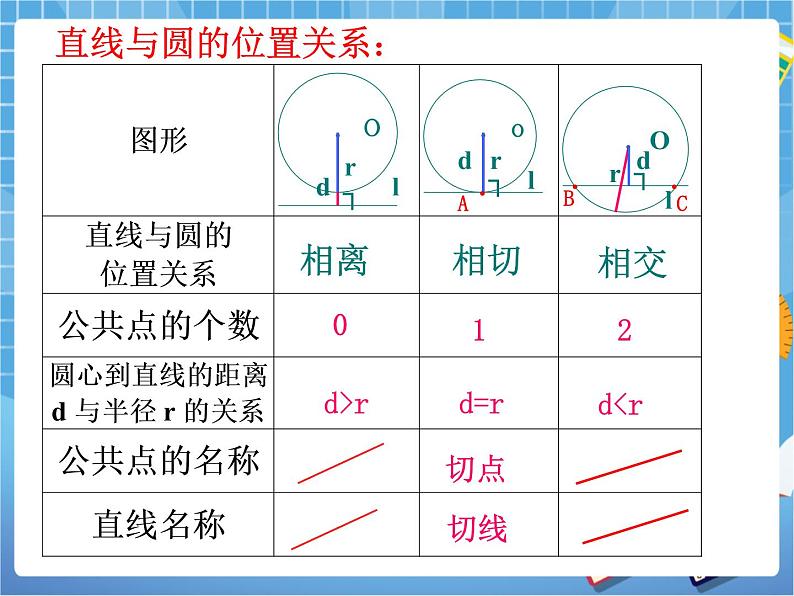
    活动内容1：回顾直线和圆的位置关系，以及切线的性质

1.直线和圆有哪几种位置关系？如何判断？

2.圆的切线具有什么性质？

3.在⊙O中,经过半径OA的外端点A作直线l⊥OA.则圆心O到直线l的距离是______,直线l和⊙O的位置关系_________.

活动内容2：引入新课

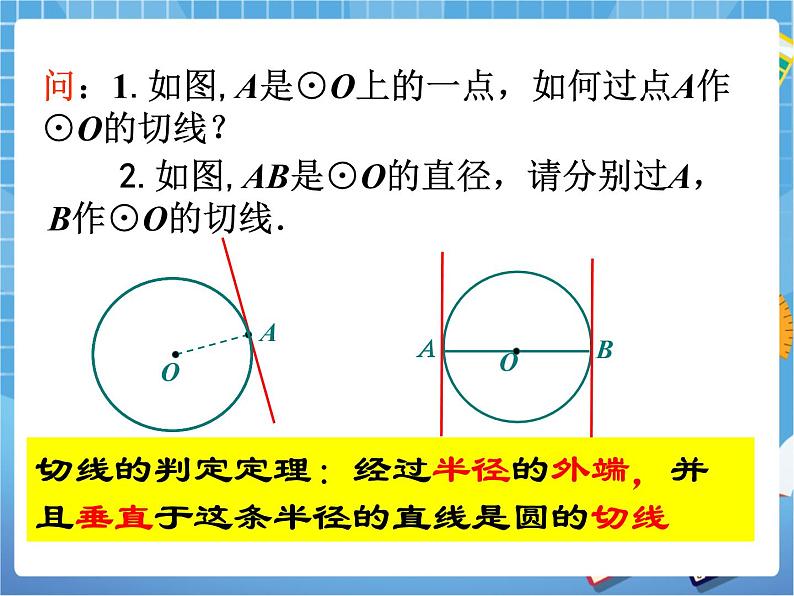
    1.如图,A是⊙O上的一点，如何过点A作⊙O的切线？

2.如图,AB是⊙O的直径，请分别过O，B作⊙O的切线．

    通过以上作图过程，我们发现满足怎样条件的直线是圆的切线？如何判断一条直线是圆的切线？本节课我们再次走进【教师板书课题：3.6直线和圆的位置关系（2）】

    处理方式：回顾上节课学习的直线与圆的位置关系，通过具体判断和作图体会如何根据d=r判断直线和圆相切，从而过渡到切线的判定定理的探究．

设计意图：让学生回顾直线与圆的位置关系，并在根据d=r判断直线和圆相切的过程中.明确用数量关系判断相切是常见的一种方法之一，在作图过程中体会判断圆的切线需要的条件，为下步归纳切线的判定定理作准备.

二、探究学习，获取新知

活动内容1：切线的判定定理

在以上作图过程中，你能否发现具有什么条件的直线是圆的切线？

处理方式：让学生观察图形，进行总结，学生可能有“经过直径一端且垂直于直径的直线是圆的切线”的说法，教师给于肯定，也有“过半径一端且垂直于半径的直线是圆的切线”的说法，教师及时引导学生补充纠正.

设计意图：通过作图的过程，学生很容易发现切线的判定定理，让学生总结的目的（1）可以让学生充分理解作图的过程和依据“d=r”,(2)让学生在自己的总结过程中准确叙述切线的判定定理.

教师强调：

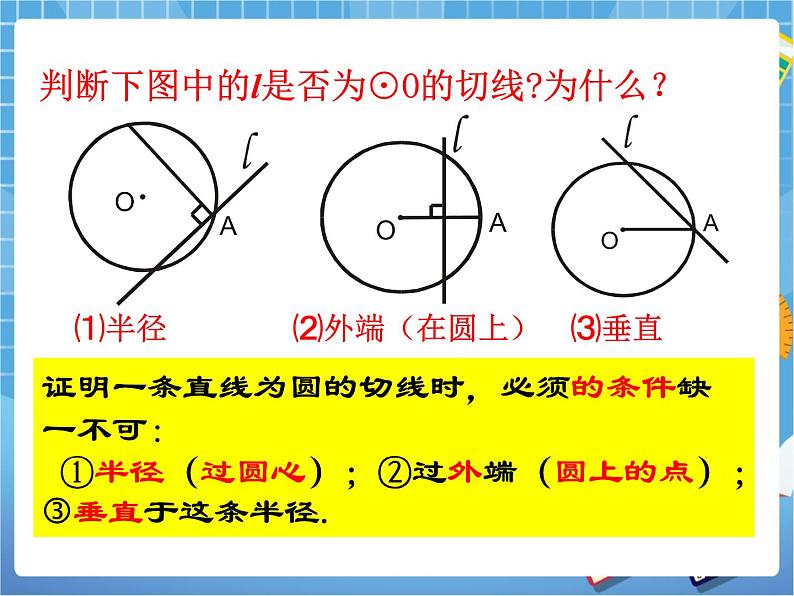
试一试：判断下图中的l是否为⊙O的切线？为什么？

处理方式：学生观察说明理由，并体会圆的切线必须满足的条件.

设计意图：通过一组不是圆的切线的判断，让学生体会圆的切线必须满足三个条件：有过圆心的线（直径或半径）；过圆上的点（直径一端或半径外端）；垂直.为下步添加辅助线判断圆的切线做准备.

活动内容2：认识三角形的内切圆

例2  如图，在ABC中，作一个圆使它与这个三角形三边都相切.

处理方式：让学生在练习本上画草图进行分析，要明确此圆需在三角形的内部，且与三角形三边相切，然后重点探究确定圆心和半径的方法，并尝试画图，同时能口述画图过程，还要让学生说明这样做的道理.

教师多媒体展示作图过程：

解：1.作∠B，∠C的平分线BE和CF，交点为I.

    2.过I作BC的垂线，垂足为D.

3.以I为圆心，以ID为半径作⊙I.

⊙I就是所求的圆.

设计意图：学生已有了作外接圆的经验，让学生自主类比作外接圆的过程进行分析，一是提高学生的自主分析能力，二是培养学生的小组合作意识.学生通过作图还可以提高动手操作的能力和说理能力.

想一想：类比前面我们学习过的外接圆，你能给这个圆和这个圆心一个名字吗？它们与外接圆和外心有何不同？

处理方式：根据圆与三角形的位置，引导学生大胆归纳内切圆和内心的概念，同时还要说明它们与外接圆、外心的不同.

设计意图：学生类比外接圆和外心的概念，总结内切圆和内心的概念，一是提高学生的归纳能力，二是让学生体会类比思想.

教师强调：

三、训练反馈，应用提升

活动内容1：切线判定定理的应用

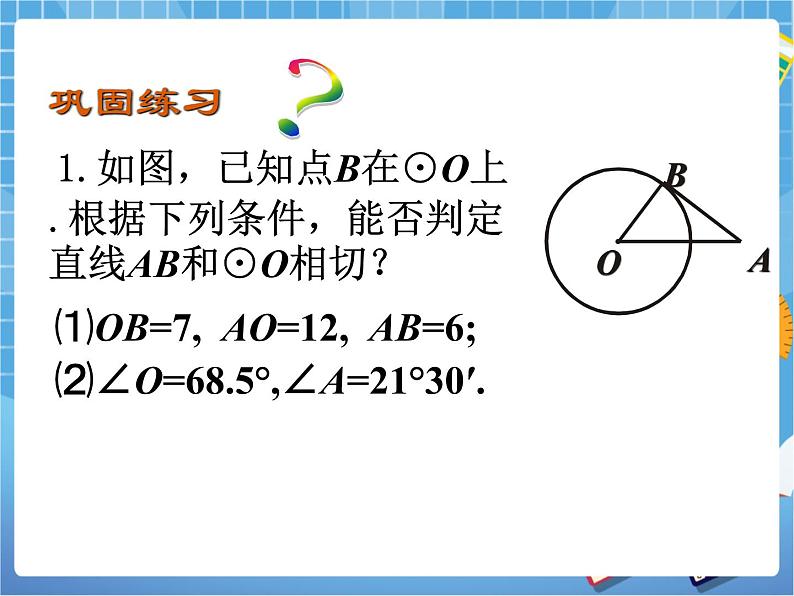
1.如图，已知点B在⊙O上.根据下列条件，能否判定直线AB和⊙O相切？

（1）OB=7,  AO=12,  AB=6

（2）∠O=68.5°,∠A=21°30′

    2.如图，AB是⊙O的直径， AT=AB，∠ABT=45°

      求证：AT是⊙O的切线.

3.已知:△ABC内接于⊙O，AB是⊙O的直径，∠CAD=∠ABC，判断直线AD与⊙的位置关系，并说明理由.

变式训练：已知:△ABC内接于⊙O，AB是⊙O的弦，∠CAD=∠ABC，判断直线AD与⊙O的位置关系，并说明理由.

4. 已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.

求证:直线AB是⊙O的切线

5.如图，点O为∠ABC平分线上一点，OD⊥AB于D，以O为圆心，OD为半径作圆.                     　

求证：BC是⊙O 的切线.

处理方式：学生口述思考过程，并说明理由.在添加辅助线的过程中体会圆的切线必须满足的三个条件，并能总结常见的辅助线作法.

设计意图：本组试题主要是巩固切线的判定定理，结合圆的切线具备的三个条件“有过圆心的线；过圆上的点；垂直”直接进行说理或添加必要的辅助线进行推理.

教师强调：在判定切线的时候,

（1）如果有已知点在圆上,则连半径，再证明垂直即可.

（2）如果没有已知点在圆上，往往过圆心作切线的垂线段，再证明d=r即可.

活动内容2：三角形内心的理解

    1.已知△ABC的内切圆⊙O与各边相切于点D，E，F，那么点O是△DEF___________线的交点.

2.如图，在△ABC中，∠A=68°，点I是内心，求∠I的度数.

处理方式：学生独立思考后，在小组内交流思考过程，再口述解题过程.

设计意图：第1题考查学生对外心和内心的区别，第2题考查学生对内心的理解.

四、回顾反思，提炼升华

通过这节课的学习，你有哪些收获？有何感想？学会了哪些方法？先想一想，再分享给大家．

处理方式：学生畅谈自己的收获！

教师强调：1.切线的判定定理：过半径外端且垂直于半径的直线是圆的切线．

    2.内切圆和内心的概念：和三角形三边都相切的圆叫做三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.

    设计意图：课堂小结是培养好学生反思、总结习惯的最好环节，只有学生养成良好的反思总结习惯，才能不断的取得进步，让学生在每堂课中体会小结的意义．

五、达标检测，反馈提高

活动内容：完成达标小卷．（多媒体出示）

A组   1.等边三角形的边长为4，则此三角形内切圆的半径为__________．

2.下列图形中不一定有内切圆的是（　　）

A.任意三角形       B.矩形       C.菱形       D.正方形

3.如图，AB是⊙O的直径，点F，C是⊙O上两点，且==，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．

    （1）求证：CD是⊙O的切线；

（2）若CD=2，求⊙O的半径．

    B组    如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，连接CD．

    （1）求证：∠A=∠BCD；

    （2）若M为线段BC上一点，试问当点M在什么位置时，直线DM与⊙O相切？并说明理由．

处理方式：学生在8分钟内独立完成后，两生分别说明思考过程，同位互换批改，不明白的问题利用1分钟时间交流、改正.

    设计意图：让学生利用当堂达标检测自己的学习效果，A组题目考查基础，给学生学习的信心和成功的体验，B组题目具有一些挑战性，考查学生综合应用知识的能力.

六、布置作业，课堂延伸

 基础作业：课本P93“随堂练习”第2题，习题3.8，第1题．

拓展作业：如图，△ABC内接于⊙O，CA=CB,CD∥AB且与OA的延长线交于点D.

（1）判断CD与⊙O的位置关系并说明理由；

    （2）若∠ACB=120°，OA=2.求CD的长.

板书设计