




高中数学人教版新课标A必修11.3.1单调性与最大(小)值课前预习ppt课件
展开
这是一份高中数学人教版新课标A必修11.3.1单调性与最大(小)值课前预习ppt课件,共21页。PPT课件主要包含了-∞+∞,-∞0,0+∞,讲解新课,⒈增函数与减函数,例题讲解,第二课时,补充例题等内容,欢迎下载使用。
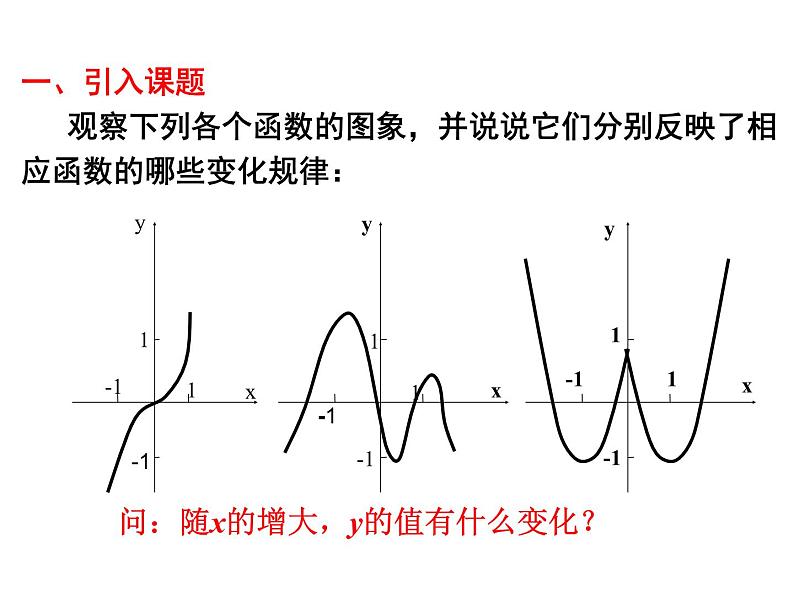
一、引入课题 观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
问:随x的增大,y的值有什么变化?
画出下列函数的图象,观察其变化规律:1.f (x) = x① 从左至右图象上升还是下降______?②在区间 ____________ 上,随着x的增大,f (x)的值随着 ________ .
2.f (x) = -x+1① 从左至右图象上升还是下降 ______?②在区间 ____________ 上,随着x的增大,f (x)的值随着 ________ .
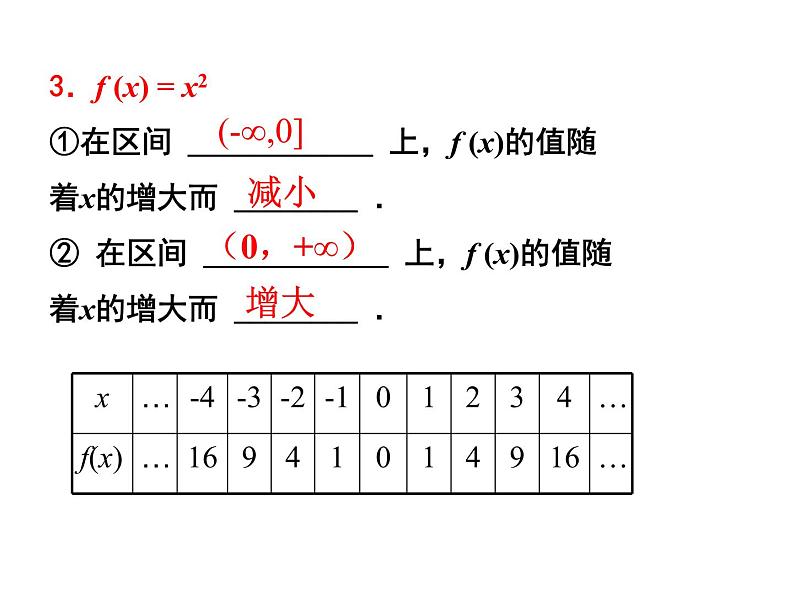
3.f (x) = x2①在区间 ____________ 上,f (x)的值随着x的增大而 ________ .② 在区间 ____________ 上,f (x)的值随着x的增大而 ________ .
定义:对于函数f(x)的定义域I内某个区间上的任意两个自变量的值x1,x2:
⑴若当x1<x2时,都有f(x1) <f(x2) ,则说f(x)在这个区间上是增函数(如图3)
⑵若当x1<x2时,都有f(x1) >f(x2) ,则说f(x)在这个区间上是减函数(如图4)
2.单调性与单调区间 如果函数y=f(x)在某个区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D 叫做y=f(x)的单调区间:
(1)这个单调区间可以是整个定义域 如y=x在定义域上是增函数, y=-x在R上是减函数
(2) 这个单调区间也可以是定义域的真子集 如y=x2在定义域上没有单调性,但在(-∞,0]是减函数,在 [0,+∞)是增函数.
(3)有的函数没有单调性区间
注意:① 函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;②必须是对于区间D内的任意两个自变量x1,x2;
③函数的单调性是相对某个区间而言,不能直接说某函数是增函数或减函数。
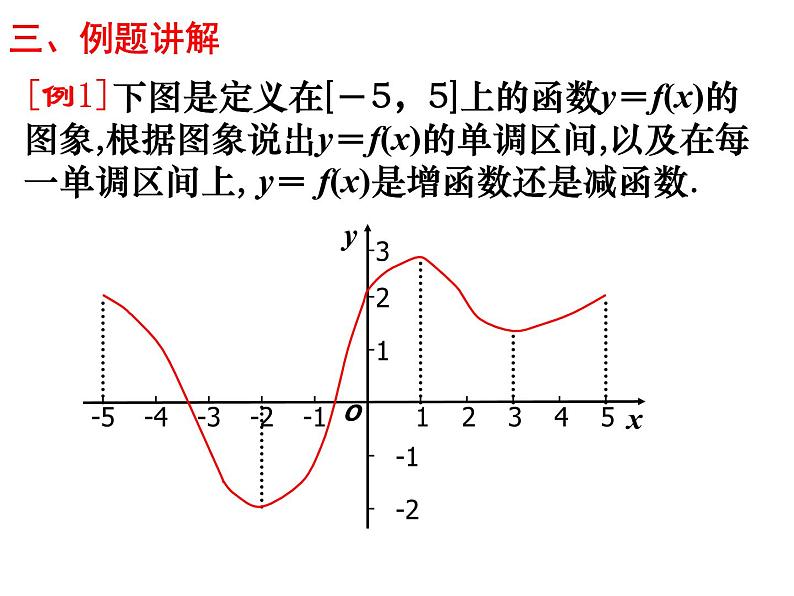
[例1]下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y= f(x)是增函数还是减函数.
书写单调区间时,注意区间端点的写法。
对于某一个点而言,由于它的函数值是一个确定的常数,无单调性可言,因此在写单调区间时,可以包括端点,也可以不包括端点。但对于某些不在定义域内的区间端点,书写时就必须去掉端点。
单调区间之间必须用“,”隔开,或者用“和”连接,但千万不能用“∪”连接,也不能用“或”,“且”连接。
思考1:指出函数 的单调区间?
例2. 指出下列函数的单调区间:
(3)判断函数 的单调性。
练习:课本P32第3题。
1.3.1 函数的单调性
练习:课本P32第3题
任取x1,x2∈(0,+∞),且x1<x2,则
∵00
1.取数:任取 ,且 ; 2.作差: ; 3.变形:通常是因式分解和配方; 4.定号:判断差 的正负; 5.下结论:指出函数 在给定的区间D上的 单调性.
练习:课本P32第4题
利用定义确定或证明函数 在给定的 区间D上的单调性的一般步骤:
证明函数 在(1,+∞)上为增函数。
作业布置:课本P39 A组第1、2、3题
课本P44,A组第9题。
例3 、若函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,求实数a的取值范围。
例2 、已知函数y=(2a-1)x+4是R上的减函数,求a的取值范围。










