2020-2021学年28.2 解直角三角形及其应用获奖ppt课件

这是一份2020-2021学年28.2 解直角三角形及其应用获奖ppt课件，共19页。PPT课件主要包含了新课引入，新知探究，例题讲解，当堂检测，拓展延申，∴BDCD2，解直角三角形，勾股定理，两锐角互余，锐角的三角函数等内容，欢迎下载使用。

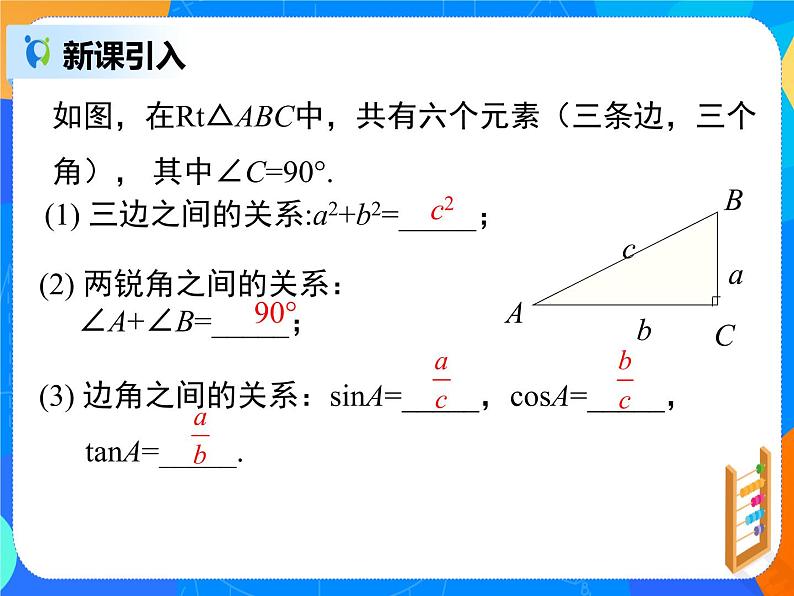
(1) 三边之间的关系:a2+b2=_____；
(2) 两锐角之间的关系： ∠A+∠B=_____；
(3) 边角之间的关系：sinA=_____，csA=_____， tanA=_____.
如图，在Rt△ABC中，共有六个元素（三条边，三个角）， 其中∠C=90°.
如图Rt△ABC中，∠C＝90°(1) 已知∠A＝75°，AB＝6，你能求出这个直角三角形的其他元素吗？（参考数据 ：sin75°≈0.97，cs75°≈0.26，tan75°≈3.73）
(2) 已知AC＝2.4，AB＝6，你能求出这个直角三角形的其他元素吗？（参考数据：cs66°≈0.4）
说明： 在直角三角形中，除直角外有5个元素（即3条边、2个锐角），只要知道其中的2个元素（至少有1个是边），就可以求出其余的3个未知元素.简记为：知二推三
什么叫解直角三角形？ 由直角三角形中的已知元素，求出其余未知元素的过程，叫作解直角三角形.
例2.如图，在Rt△ABC中，∠C＝90°，∠B＝35°，b=20，解这个直角三角形 (结果保留小数点后一位)（参考数据 tan35°≈0.700，sin35°≈0.573）
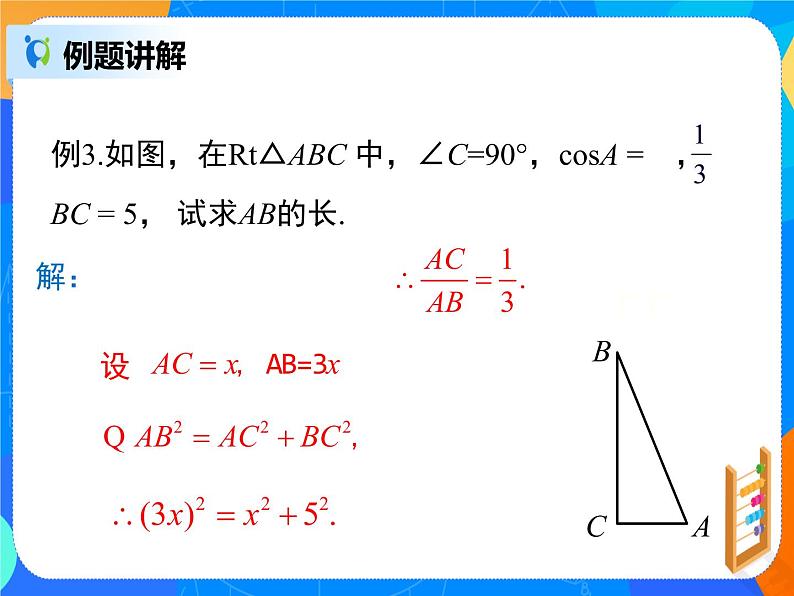
例3.如图，在Rt△ABC 中，∠C=90°，csA = ，BC = 5， 试求AB的长.
1，在Rt△ABC中，∠C＝90°，a = 30，b = 20，根据条件解这个直角三角形 （ 参考数据：tan56.3°≈1.5 tan33.7°≈0.67）
解 ∵∠C＝90°a = 30，b = 20，
3. 在Rt△ABC中，∠C=90°，∠B=30°， AB=8，则BC的长是 ( )
2. 在RT△ABC中，∠C=90°，a，b，c分别是∠A， ∠B，∠C的对边，则下列各式正确的是 ( ) A. b=a·tanA B. b=c·sinA C. b=c·csA D. a=c·csA
5. 如图，在菱形ABCD中，AE⊥BC于点E，EC=4， sinB＝ ，则菱形的周长是 ( ) A．10 B．20 C．40 D．28
如图△ABC中， AC = 4，∠ A=30°，∠ACB=105°求 AB 和 BC 的长．
提示：作CD⊥AB于点D，在Rt△ACD与Rt△CDB中，根据锐角三角函数的定义，即可求出 CD，AD，BD 的长，从而AB 和 BC 的长．
在Rt△CDB中，∵∠DCB=∠ACB－∠ACD=45°，
解：如图，作CD⊥AB于点D，
在Rt△ACD中，∵∠A=30°，∴∠ACD=90°-∠A=60°，
解法：只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素
（一） 解直角三角形的基本题型
（2）已知一条边和一个锐角
（1）已知两条边
（3）已知一条边和一个锐角三角函数值
（二）非直角三角形中遇30°，45°，60°等特殊角时，往往需要通过添加高或垂线段，把问题转化到直角三角形中去解决。